QC検定2級 公式集

公開日2022年7月24日 最終更新日 2022年8月26日
みなさんこんにちは、michiです。
この記事では、QC検定2級に出てくる公式をまとめています。
タイトルをクリックすると、各公式の説明記事へ飛びます。
スキマ時間に確認して、試験本番で公式を使いこなせるようにしましょう!
\[\]
結構覚えなきゃいけない公式が多いですよ!
(;´・ω・)
\[\]
\[\]
\[S=\sum (x_i – \bar{x}) \qquad or \qquad S=\sum x_i^2 -\frac{(\sum x_i)^2}{n} \]
- \(\sum\):合計を表す
- \(x_i\) :各測定値
- \(\bar{x}\):平均値
- \(n\):サンプル数
覚え方:「庭にひくサンプル分のワニ」
\[\]
\[V=\frac{S}{n-1} \qquad =\frac{平方和}{自由度}\]
- \(n-1\):自由度 サンプル-1 の数
\[\]
\[\sigma = \sqrt{V} \qquad =\sqrt{不偏分散}\]
\[\]
\[CV=\frac{\sigma}{\bar{x}}\qquad =\frac{標準偏差}{平均値}\]
覚え方:Cat Video(CV)は平均以上にへんさ
\[\]
\[Z=\frac{x_i – \bar{x}}{\sigma}\]
※計算した\(Z\) を正規分布表と照らし合わせ、確率を読み取るする。
\[\]
二項分布の確率
\[ P(x) = \scriptsize{n}\large{C}\scriptsize{x} × p^ x × (1-p)^{n-x} \]
- 二項分布の期待値:\(E(X)=np\)
- 二項分布の分散:\(V(X)=np(1-p)\)
\[\]
ポアソン分布の確率
\[P(x)=\frac{λ^x・e^{-λ}}{x!}\]
- ポアソン分布の期待値:\(E(x)=λ\)
- ポアソン分布の分散:\(V(x)=λ\)
覚え方:「平常かい?異常まいった、貝びっくりΣ(・ω・ノ)ノ!」
\[\]
期待値の性質
- \(E(c) = c\)
- \(E(X+c) = E(X) + c\)
- \(E(cX) = cE(X)\)
- \(E(X+Y) = E(X) + E(Y) \qquad \)分散の加法性
分散の性質
- \(V(c) = 0\)
- \(V(X+c) = V(X)\)
- \(V(cX) = c^2V(X)\)
- \(V(X+Y) = V(X) + V(Y) \qquad \)分散の加法性
- \(V(X+Y) = V(X) + V(Y)+2Cov(X,Y) \quad \)分散の加法性が成り立たない場合
\[\]
\[Z\qquad =\frac{\bar{x}-μ}{\sqrt{\frac{σ^2}{n}}} \qquad=\frac{標本平均-母平均}{\sqrt{\frac{母分散}{サンプル数}}}\]
\[\]
\[\mu\qquad = \bar{x} \pm Z\left(\frac{\alpha}{2} \right) \times \frac{\sigma_o}{\sqrt{n}}\]
- \bar{x}:点推定値
- \(Z()\):正規分布表から求める係数(\(K_p\))
- \(\alpha\):有意水準
- \(\sigma_0\):母分散
- \(n\):サンプル数
\[\]
\[t\qquad =\frac{\bar{x}-μ}{\sqrt{\frac{V}{n}}} \qquad=\frac{標本平均-母平均}{\sqrt{\frac{不偏分散}{サンプル数}}}\]
\[\]
\[\mu\qquad = \bar{x} \pm t(\phi,\alpha) \times \sqrt{\frac{V}{n}}\]
- \(t()\):t表から求める係数
- \(\phi\):自由度
- \(\alpha\):有意水準
- \(V\):不偏分散
- \(n\):サンプル数
\[\]
\[χ^2 \qquad = \frac{S}{\sigma_0^2} \qquad = \frac{平方和}{母分散}\]
\[\]
\[\frac{S}{χ^2(Φ,\frac{α}{2})} ≦ σ^2 ≦ \frac{S}{χ^2(Φ,1-\frac{α}{2})}\]
- \(S\):平方和
- \(\phi\):自由度
- \(\alpha\):有意水準
\[\]
\[F=\frac{V_A}{V_B} \qquad ただし\frac{V_A}{V_B}>1\]
\[\]
\[上側の棄却限界値=\frac{S}{χ^2(8,0.975)}\]
\[下側の棄却限界値=\frac{S}{χ^2(8,0.025)}\]
※下側の棄却限界値の求め方は下式 詳細は こちら から
\[棄却限界値 F(Φ_2,Φ_1:0.975)=\frac{1}{棄却限界値 F(Φ_1,Φ_2:0.025)}\]
\[\]
\[Z=\frac{p-P_0}{\sqrt{\frac{P_0(1-P_0)}{n}}}\]
- \(p\):注目する事象の発生確率
- \(P_0\):もともと想定していた事象の発生確率
- \(n\):サンプル数(データ数)
\[\]
\[Z=\frac{p_A-p_B}{\sqrt{\bar{p}(1-\bar{p})(\frac{1}{n_A}+\frac{1}{n_B})}}\]
- \(\bar{p}\):AとBの集団を合わせて、注目する事象の発生する確率
- \(n_A\):集団Aのサンプル数
- \(n_B\):集団Bのサンプル数
- \(p_A\):集団Aで注目する事象の発生する確率
- \(p_B\):集団Bで注目する事象の発生する確率
\[\bar{p}=\frac{x_A+x_B}{n_A+n_B}\]
- \(x_A\):集団Aで注目する事象の発生する回数
- \(x_B\):集団Bで注目する事象の発生する回数
\[\]
\[Z=\frac{λ-λ_0}{\sqrt{\frac{λ_0}{n}}}\]
- \(λ\):注目する事象の発生確率
- \(λ_0\):もともと想定していた事象の発生確率
- \(n\):サンプル数(データ数)
\[\]
\[Z=\frac{λ_A-λ_B}{\sqrt{λ×(\frac{1}{n_A}+\frac{1}{n_B})}}\]
- \(λ_A\):集団Aにおける事象の発生確率
- \(λ_B\):集団Bにおける事象の発生確率
- \(n_A\):集団Aのサンプル数(データ数)
- \(n_B\):集団Bのサンプル数(データ数)
\[\]
\[χ^2=\displaystyle \sum_{i=1}^m \sum_{j=1}^n \frac{(f_{ij}-e_{ij})^2}{e_{ij}} \]
- \(f_{ij}\):観測度数
- \(e_{ij}\):期待度数
検定統計量の棄却域は右側のみを考える!
\[\]
\[r=\frac{S_{xy}}{\sqrt{S_x}\sqrt{S_y}}\]
- \(r\):相関係数
- \(S_{xy}\):\(x\)、\(y\) の偏差積和
- \(S_x\):\(x\) の平方和
- \(S_y\):\(y\) の平方和
\[\]
\[R=r^2=\frac{(S_{xy})^2}{S_x \times S_y}\]
- \(R\):寄与率
- \(r\):相関係数
- \(S_{xy}\):\(x\)、\(y\) の偏差積和
- \(S_x\):\(x\) の平方和
- \(S_y\):\(y\) の平方和
\[\]
\[S_{xy}=\sum{x_i y_i}-\frac{(\sum x_i)(\sum y_i)}{n}\]
\[\]
\[\alpha = \bar{y} – \beta \bar{x} \qquad \beta = \frac{S_{xy}}{S_x}\]
- \(\alpha\) :回帰式の切片
- \(\bar{y}\):データ \(y\) の平均値
- \(\bar{x}\):データ \(x\) の平均値
- \(\beta\):回帰式の回帰係数
- \(S_{xy}\):偏差積和
- \(S_x\):\(x\) の平方和
\[\]
\[S_T=S_y \qquad S_R=\frac{(S_{xy})^2}{S_x} \qquad S_E=S_T-S_R=S_y-\frac{(S_{xy})^2}{S_x}\]
- \(S_T\):全体の変動
- \(S_R\):回帰による変動
- \(S_E\):残差による変動
- \(S_{xy}\):偏差積和
- \(S_x\):\(x\) の平方和
- \(S_y\):\(y\)の平方和
\[\]
回帰分析の分散分析表
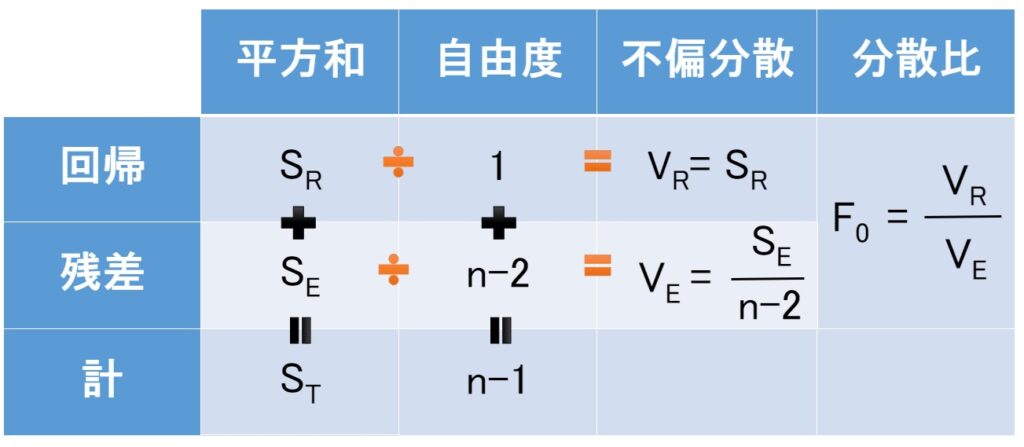
※回帰の自由度は 1 になります。
\[\]
\[修正項(CT)=\frac{(データの合計)^2}{データ数}\]
\[総平方和S_T = \sum (データの二乗)- 修正項(CT)\]
\[級間平方和S_A=\displaystyle \sum_{i=1}^n \frac{(A_i の合計)^2}{A_i のデータ数} – 修正項(CT)\]
\[誤差平方和S_E=総平方和S_T – 級間平方和S_A\]
\[\]
一元配置実験の分散分析表

※誤差の自由度は、全体の自由度から因子の自由度を引いて求めます。
\[\]
交互作用がない場合
\[修正項(CT)=\frac{(データの合計)^2}{データ数}\]
\[総平方和S_T = \sum (データの二乗)- 修正項(CT)\]
\[級間平方和S_A=\displaystyle \sum_{i=1}^n \frac{(A_i の合計)^2}{A_i のデータ数} – 修正項(CT)\]
\[級間平方和S_B=\displaystyle \sum_{i=1}^n \frac{(B_i の合計)^2}{B_i のデータ数} – 修正項(CT)\]
\[誤差平方和S_E=総平方和S_T – 級間平方和S_A- 級間平方和S_B\]
\[\]
交互作用がある場合
\[修正項(CT)=\frac{(データの合計)^2}{データ数}\]
\[総平方和S_T = \sum (データの二乗)- 修正項(CT)\]
\[級間平方和S_A=\displaystyle \sum_{i=1}^n \frac{(A_i の合計)^2}{A_i のデータ数} – 修正項(CT)\]
\[級間平方和S_B=\displaystyle \sum_{i=1}^n \frac{(B_i の合計)^2}{B_i のデータ数} – 修正項(CT)\]
\[級間平方和S_{AB}==\displaystyle \sum_{i=1}^n \frac{(AB二元表のデータ)^2}{繰り返し数} \qquad – 修正項(CT)\]
\[交互作用 S_{A \times B}=S_{AB}-S_A-S_B\]
\[誤差平方和S_E=総平方和S_T – 級間平方和S_{AB}\]

\[\]
有効反復係数\(n_E\)
\[n_E=\frac{abn}{a+\phi_A+\phi_B+\phi_{A \times B}}\]
- \(a\):Aの水準数
- \(b\):Bの水準数
- \(n\):繰り返しの数
- \(\phi_A\):Aの自由度
- \(\phi_B\):Bの自由度
- \(\phi_{A \times B}\):交互作用\(A \times B\)の自由度
\[\]
信頼度95%の母平均信頼区間
\[\mu \pm t(\phi_E,0.05)\times \sqrt{\frac{V_E}{n_E}} \]
- \(\mu\):母平均の点推定値
- \(t()\):t表の係数
- \(\phi_E\):誤差の自由度
- \(V_E\):誤差の不偏分散
- \(n_E\):有効反復係数
\[\]
\(\bar{x}\) 管理図
- 上方管理限界線:\(\bar{\bar{x}}+A_2 \times \bar{R}\)
- 中心線:\(\bar{\bar{x}}\)
- 下方管理限界線:\(\bar{\bar{x}}-A_2 \times \bar{R}\)
\(R\) 管理図
- 上方管理限界線:\(D_4 \times \bar{R}\)
- 中心線:\(\bar{R}\)
- 下方管理限界線:\(D_3 \times \bar{R}\)
- ※下方管理限界線は、サンプル数が6個以下の場合は設けない
\[\]
\(\bar{x}-R\) 管理図の係数表は下図の通り(計数表は覚える必要なし)

\[\]
- 上方管理限界線:\(\bar{p} + 3\sqrt{\frac{\bar{p}(1-\bar{p})}{n}}\)
- 中心線:\(\bar{p}=\frac{不良個数の総和}{総データ数}\)
- 下方管理限界線:\(\bar{p} – 3\sqrt{\frac{\bar{p}(1-\bar{p})}{n}}\)
\[\]
- 上方管理限界線:\(n\bar{p} + 3\sqrt{n\bar{p}(1-\bar{p})}\)
- 中心線:\(n\bar{p}=\frac{不良個数の総和}{群の数}\)
- 下方管理限界線:\(n\bar{p} – 3\sqrt{n\bar{p}(1-\bar{p})}\)
\[\]
- 上方管理限界線:\(\bar{c}+3\sqrt{\bar{c}}\)
- 中心線:\(\bar{c}=\frac{不適合数の総和}{群の数}\)
- 下方管理限界線:\(\bar{c}-3\sqrt{\bar{c}}\)
\[\]
- 上方管理限界線:\(\bar{u}+3\sqrt{\frac{\bar{u}}{n}}\)
- 中心線:\(\bar{c}=\frac{不適合数の総和}{サンプルの大きさの総和}\)
- 下方管理限界線:\(\bar{u}-3\sqrt{\frac{\bar{u}}{n}}\)
\[\]
\[C_p:\frac{規格の上限 – 規格の下限}{6 \times \sigma}\]
\[C_{pk}:\frac{規格の上限 – 平均値}{3 \times \sigma} \qquad or \qquad \frac{平均値 – 規格の下限}{3 \times \sigma}\]
※\(C_{pk}\) は小さいほうを採用する
\[\]
\[MTTF(平均故障時間)=\frac{総稼働時間}{総故障件数}\]
\[MTBF(平均故障間隔)=\frac{総稼働時間}{総故障件数}\]
\[\lambda(故障率)=\frac{総故障件数}{総稼働時間}=\frac{1}{MTBF}\]
\[\]
\[MTTR(平均修復時間)=\frac{総修理時間}{総修理件数}\]
\[アベイラビリティ(A)=\frac{動作時間}{時間全体}=\frac{動作時間}{動作時間+修理時間}=\frac{MTBF}{MTBF+MTTR}\]
\[\]
毎日見て、目に焼き付けましょう!
(◉ω◉`) ジーーーッ
\[\]