正規分布表のミカタ

公開日2020年2月26日 　最終更新日 2022年4月29日

みなさんこんにちは、michiです。

前回の記事では、標準偏差を利用した統計的な処理方法を学びました。

他にも標準偏差の利用方法はないのでしょうか？

QC検定に出題される標準偏差を利用した代表的なものに、正規分布表があります。

キーワード　「正規分布表」　「確率変数」　

\[\]

①正規分布表の見方　KpからPを求める表

前回学んだ変動係数はQC検定に出ますが、出現頻度でいうと「正規分布表」のほうがたくさん出てきます。

正規分布表は下表のようなものです。

\[\]

KpからPを求める表　表1

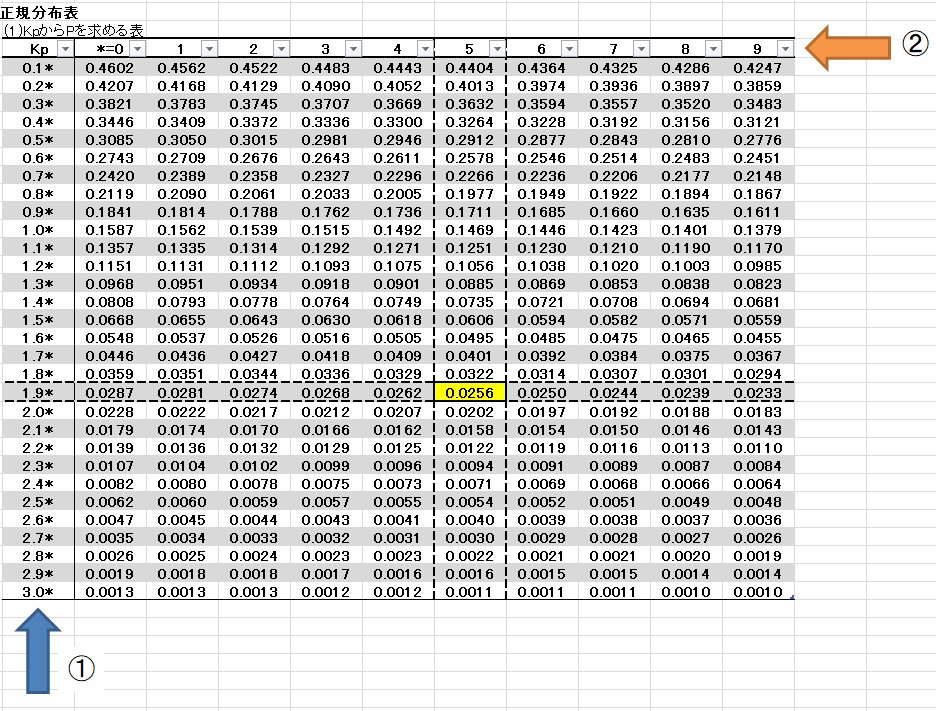
Kpは確率変数と呼ばれています。Pは確率です。

確率はなんとなく意味がわかりますが、確率変数は初耳の人も多いのではないでしょうか。

ウィキペディアによると、確率変数は「確率論ならびに統計学において、起こりうる事柄に割り当てている値をとる変数」とあります。https://ja.wikipedia.org/wiki/確率変数

(。´･ω･)?

\[\]

簡単に言うと、「確率変数は、ある確率にわりあてられた値」　です。

QC検定にでてくる問題では、直接確率をもとめるません。

いったん確率変数をもとめてから、確率を求める問題がたくさんでてきます。

\[\]

表1は、

\[平均値（期待値）=0、分散＝1^2 \]

の正規分布にしたがう「標準正規分布表」 といいます。この条件を

\[N(0、1^2)\]

と一般的に表現します。

(´・∀・｀)ﾍｰ

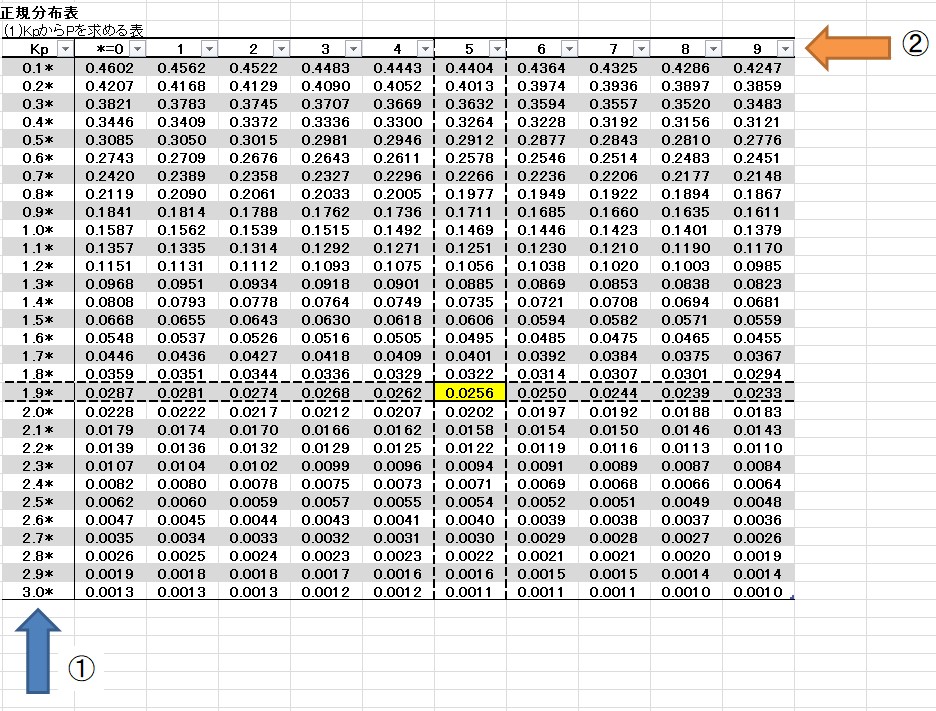
※表１では、確率変数　Kp=1.95　のとき、　確率 P=0.0256 (2.56%)となります。

一の位と小数第一位は左の列①の数値（=1.9）を、少数第二位は上の行②の数値(=5)をみて、その交点が求める確率になります。（＊は少数第二位を表す）

上のグラフは標準正規分布表です。横軸の確率変数Kp=1.95　以上のときの確率（合計値）は黄色で表される範囲で、P=0.0256　となります。

※グラフは±3の範囲のみ表示していますが、実際の分布は±∞まであります。

\[\]

②データの標準化

さきほどの表1は、測定されたデータが正規分布する場合、

\[平均値（期待値）=0、分散＝1^2 \]

に変換することで、利用可能になります。

なぜ変換が必要なのでしょうか？　

(。´･ω･)?

\[\]

現実に得られるデータは、種類が無限にあるため、代表値の平均値や分散の組合せも無限にあります。

それらのデータに対応する正規分布表をひとつずつ作るのはかなりめんどくさいです。

(´･ω･`)

\[\]

そこで、ひとつの基準となる正規分布表に各データを当てはめるようにデータを変換することで、効率的にデータ解析をします。

このデータの変換を「標準化」または「基準化」といいます。

標準化したデータの確率変数　Z　は、

\[Z= \frac{測定値 – 平均値}{ 標準偏差(=\sqrt{分散})} \]

でもとめます。

\[\]

③データ標準化式の意味

考え方１

さて、もう一度測定データの標準化の式を見てみましょう

\[Z= \frac{測定値 – 平均値}{ 標準偏差(=\sqrt{分散})} \]

この式を、「測定値＝　」の形に変換すると

\[測定値= Z　× 標準偏差(=\sqrt{分散})　+ 平均値\]

となります。　Zは標準正規分布の確率変数でした。

つまり測定値とは、標準正規分布の確率変数を標準偏差倍し、平均値を足した値　となります。

実は、この考え方は正規分布をするすべてのデータにいえます。

\[\]

また、確率変数Zの式を素直に読むと

\[Z= \frac{測定値 – 平均値}{ 標準偏差(=\sqrt{分散})} \]

「標準偏差あたりの測定値の平均値からずれ」　を意味します。

言い換えると、「測定データの分布のばらつき具合からみて、注目している測定データは平均にどれくらい近いの？」　ということになります。

標準化の意味と確率変数Zの意味が、なんとなくわかってきたのではないでしょうか。

(-ω-;)ウーン

\[\]

考え方2

標準化とは、任意の正規分布をするデータを、平均値\(0\) 分散\(1^2\) の標準正規分布\(N(0,1^2)\)に変換することです。

\[\]

先ほどと同様に、式の意味を考えていきましょう。

\[Z= \frac{測定値 – 平均値}{ 標準偏差(=\sqrt{分散})} \]

まず分子の「測定値ー平均値」 ですが、この変換によって、正規分布の中心値（平均値）が0になるように移動できます。

例えば「90,100,110」のデータ群から、平均値100を引くと「-10,0,10」になりますよね。

\[\]

つぎに分布の幅を分散(\(σ^2=1\))　になるように変換します。

ここで分母の「\(σ\)」 ですが、記事「不偏分散ではだめ？なぜ標準偏差？」から下図を持ってきました。

（ちょっと図だとずれていますが・・・）

標準偏差\(σ\) は、分布の幅によって様々な値をとるのですが、標準正規分布では標準偏差\(σ=1\) となります。

\[\]

「平均値0 (\(x-μ\) の計算によって)、分布の幅\(σ\)の正規分布」　の分布の幅を 1 にするにはどうすればよいのでしょうか？

(。´･ω･)?

単純ですが、標準偏差\(σ\) で割ります！

\[\]

以上から　確率変数\(x\) が、\(N(μ,σ^2)\)に従う時の標準化の式は、

\[Z= \frac{測定値 – 平均値}{ 標準偏差(=\sqrt{分散})} \]

この変換を行うことで、平均値\(0\) 分散\(1^2\) の標準正規分布\(N(0,1^2)\)に変換することが可能となります。

\[\]

④データの標準化　例題

具体例を解いてみましょう。

\(N(8、3^2)\)　の正規分布で、測定値が15.56　より大きい値が得られる確率をもとめよ　

\[\]

測定値は15.56、平均値は 8、標準偏差は 3　なので

\[Z= \frac{測定値 – 平均値}{ 標準偏差(=\sqrt{分散})} = \frac{15.56 – 8}{3} = 2.52\]

表1の標準正規分布で確率変数Kp=2.52 の確率をもとめると、P=0.3094

つまり、30.94% の確率で15.56 より大きい値が得られるという結果になります。

\[\]

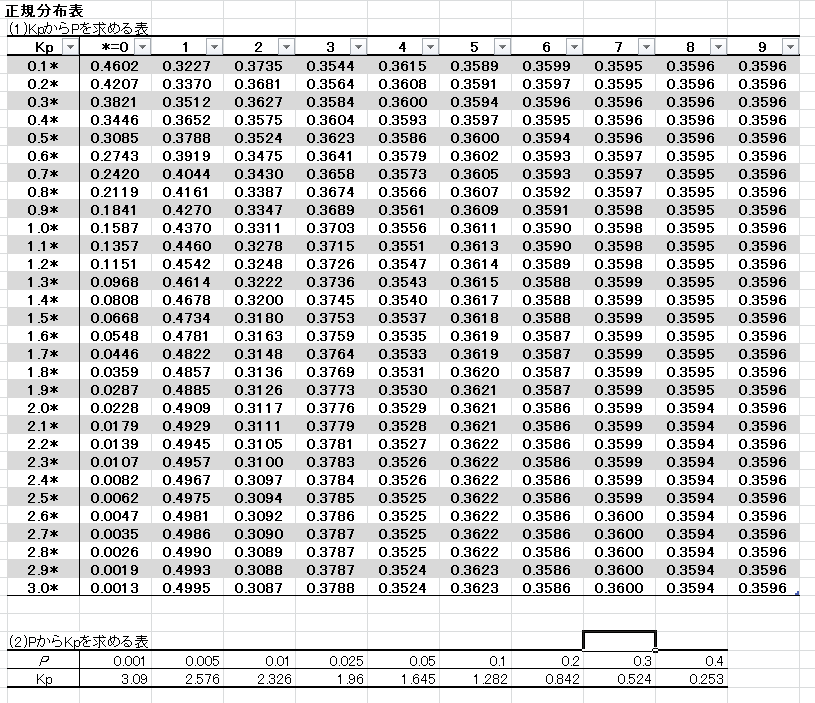
⑤正規分布表の見方　PからKpを求める表

先ほどまでは、得られたデータの分布から確率変数Kpをもとめ、確率Pをもとめました。

しかし、QC検定には「検定」や「推定」を問う問題がでてきます。

(。´･ω･)?

\[\]

細かい説明はここでは省きますが、「検定」では、仮説が〇％の確率で正しい場合の確率変数をもとめます。

下の表２　がPからKpを求める表です。

\[\]

表１のKpからPを求める表に比べるとかなりあっさりしていますね。

なぜこれだけあっさりとしているかというと、問われる「〇％で正しい確率」は基本的に5%だからです。

仮説が5%の確率で正しい場合の確率変数Kp は 1.645　です。

注）問題によっては、確率変数 Kp =1.960 の場合もあります。

\[\]

まとめ

①確率変数Kpから確率Pを求める表は、Kpの値を縦軸と横軸に分解

②データの「標準化」で、色々なデータを標準正規分布表で評価可能に

③データの標準化は「ばらつきの幅当たりの平均値からのずれ」を計算している

④例題といてみた

⑤確率Pから確率変数Kpを求める表はあっさり。そして基本5%

\[\]

「検定」と「推定」に関しては別記事にまとめます。

今回はここまでです。

次回は工程能力指数について勉強していきましょう！

⇒オススメ書籍はこちら

⇒サイトマップ