平均値に関する検定１:正規分布

公開日2020年5月3日 　最終更新日 2022年7月17日

みなさんこんにちは、ｍichiです。

前回は検定について学びました。今回は平均値の検定について学んでいきたいと思います。

記事「正規分布表のミカタ」と一部重なるところもありますが、合わせてご参考ください。

キーワード：「正規分布」「統計量」「正規分布表」

①正規分布を使った検定

今回のテーマ「平均値に関する検定」では、正規分布をする集団について考えます。

（QC検定2級のレベルでは、基本的に取り扱う母集団は正規分布にしたがいます）

\[\]

母集団から標本を抽出し、その平均値を評価するには、二つの統計量がありました。

統計量 \(Z\)　と統計量 \(t\)　です。二つの違いは覚えていますか？

(。´･ω･)?

・・・　二つの違いは以下のとおりです。

• 統計量\(Z\) は、正規分布から得られる統計量で、母分散が 既知
• 統計量\(t\) は、\(t\) 分布から得られる統計量で、母分散が 未知

今回は、母分散が既知の場合の正規分布から統計量を計算する場合について勉強していきます。

\[\]

②両側検定の正規分布

直接例題を解いたほうが理解が早いと思うので、早速とりかかりましょう。

\[\]

問）母平均 \(μ=20.0\)、母分散\(σ^2=4.0\) の母集団から、\(n=9\)個のサンプルを抽出しました。サンプルの標本平均を調べると、\(\bar{x}=18.8\) だった。

この時、母平均に対し標本平均は変化したか？第一種の誤りを5%として答えてね。

(。´･ω･)?

\[\]

いきなり問題を解く前に、問われているもの何か、以下の三つのキーワードをチェックしてください。

• 平均の変化か、ばらつき（分散）の変化か
• 変化の有無か、大小関係か
• 母分散が既知か、不偏分散のみが既知か

今回の問題は「平均の変化、変化の有無、母分散が既知」がキーワードになります。

そのため、正規分布の統計量\(Z\) を使います。

\[\]

すると、

今回の帰無仮説は「母平均に対し、標本平均の変化がない：\(μ=\bar{x}\)」で、

対立仮説は「母平均に対し、標本平均の変化がある：\(μ≠\bar{x}\)」　です。

\[\]

統計量\(Z\)　は標準化することで得られるので・・・

\[Z\qquad =\frac{\bar{x}-μ}{\sqrt{\frac{σ^2}{n}}} \qquad=\frac{標本平均-母平均}{\sqrt{\frac{母分散}{サンプル数}}}\]

今回の問題の数値をあてはめると

\[Z\qquad =\frac{\bar{x}-μ}{\sqrt{\frac{σ^2}{n}}} \]

\[\qquad=\frac{18.8-20}{\sqrt{\frac{4}{9}}}\]

\[=\frac{-1.2}{\frac{2}{3}}\qquad\]

\[= -1.8\]

\[\]

え、マイナス!?　Σ(･ω･ﾉ)ﾉ！

マイナスがついてしまいました。しかしご安心を、間違えてはいません。

\[\]

両側検定では、期待値付近（中心付近）に採択域があり、両サイドに棄却域がありました。

標準化すると、採択域の中心は　0　になります。

つまり、マイナスの領域が発生します。

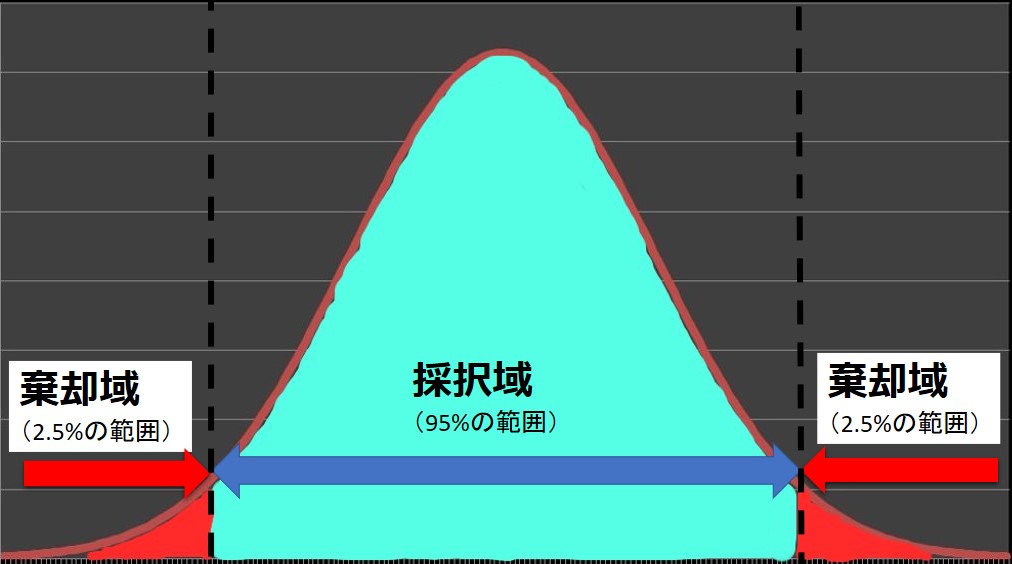
今回の問題は、「母平均に対し、標本平均に変化があったか」です。

計算結果がプラスだろうとマイナスだろうと、「統計量\(Z\)が　採択域内 or 棄却域内」に注目しましょう

φ(´･ω･｀)ﾒﾓﾒﾓ。

\[\]

さて、結局のところ計算結果の統計量\(Z=-1.8\)　が採択域なのか棄却域なのかはどのように判断すればよいのでしょうか？

ここで、「正規分表のミカタ」でサラッと説明した「ＰからKpを求める表」を使います。

\[\]

この記事出てきた、確率変数Kpが棄却限界値になります。

この表を見ると、今回の第一種の誤り5%の値は P=0.05　だから、

今回の棄却限界値は・・・1.645　!

\[\]

と思いそうですが、間違いです！

ｶﾞｯﾋﾞ――ﾝ∑(ﾟωﾟﾉ)ﾉ

\[\]

両側検定の場合は、棄却域が採択域の両サイドにあり「あわせて5%」でした。

つまり、片側の棄却域は（左右対称なので）2.5%　となります。

さらに、「ＰからKpを求める表」にはプラス側の値（絶対値）しか書かれていません。

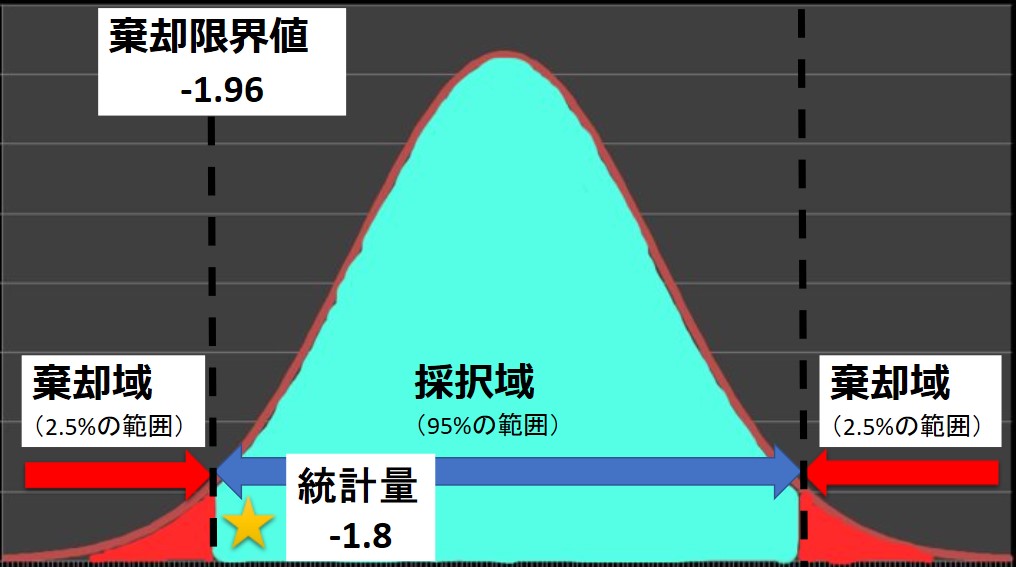
よって、棄却限界値は　P = 0.025　の値で　Kp = 1.96　、今回はマイナス側の棄却限界値が知りたいので、　「Kp = -1.96」　が棄却限界値となります。

\[\]

確率変数（=棄却限界値）Kp = -1.96　＜　統計量\(Z\)= -1.8　ですので、統計量\(Z\)　は採択域内にあると判断されます。

よって、帰無仮説「母平均に対し、標本平均の変化がない：\(μ=\bar{x}\)」が採択され、「平均値は変化したとは言えない」　と判断されます。

※マイナスの大小関係が分かりにくい場合は、0に近いほうが採択域と覚えましょう。

\[\]

③片側検定の正規分布

さて、今度は片側検定で考えてみましょう。

基本パラメータは同じにします。

問）母平均 \(μ=20.0\)、母分散\(σ^2=4.0\) の母集団から、\(n=9\)個のサンプルを抽出しました。サンプルの標本平均を調べると、\(\bar{x}=18.8\) だった。

この時母、平均に対し標本平均は小さくなったか？第一種の誤りを5%として答えてね。

\[\]

今回も問題に取り掛かる前に、問われているもの何か、以下の三つのキーワードをチェックしてくみましょう。

• 平均の変化か、ばらつき（分散）の変化か
• 変化の有無か、大小関係か
• 母分散が既知か、不偏分散のみが既知か

今回の問題は「平均の変化、大小関係、母分散が既知」がキーワードになります。この場合も同様に正規分布の統計量\(Z\) を使います。

問題に一部変更点があります。

今回の帰無仮説は「母平均に対し、標本平均の変化がない：\(μ=\bar{x}\)」で同じですが、

対立仮説は「母平均に対し、標本平均は小さくなった：\(μ>\bar{x}\)」　です。

先ほどと同じように統計量\(Z\)　を計算してみましょう。

\[Z\qquad =\frac{\bar{x}-μ}{\sqrt{\frac{σ^2}{n}}} \]

\[=-1.8\]

パラメータ自体は同じ値ですので、同じ結果になりました。

\[\]

さて、今回は「小さくなったか」と大小関係を問われているので、片側検定になります。

片側検定では棄却域は片側のみに現れました。先ほどと同様に「ＰからKpを求める表」を使うと・・・

この表を見ると、今回の第一種の誤り5%の値は P=0.05　だから、

今回の棄却限界値は・・・1.645　?!

(。´･ω･)?

\[\]

うーん・・・おしい間違いです！

片側検定では棄却域は片側のみに分布するので、棄却域限界値の片側が採択域（95%の範囲）、もう一方が棄却域（5%の範囲）となります。

よって、棄却限界値の絶対値は Kp=1.645　となります。

ここまでは良いと思います。

(σﾟ∀ﾟ)σ

\[\]

今回は「小さくなったか」が問われているので、棄却域はマイナス側にのみ存在します。

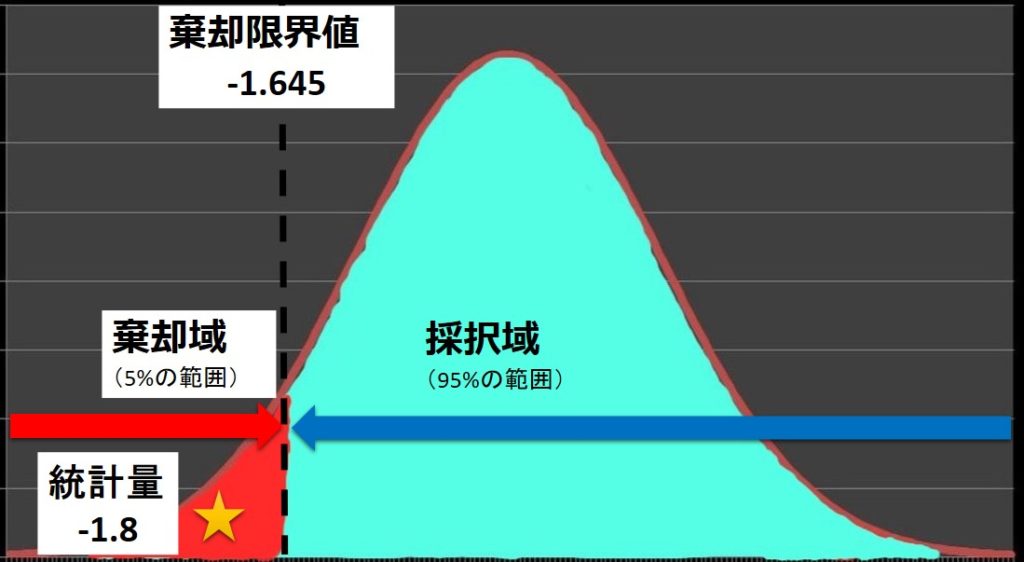
棄却限界値は　Kp= -1.645　となります。

※「なぜ棄却域がマイナス側にあるのか？」は、記事「検定とは」をご参考ください。

\[\]

棄却限界値がわかりましたので、今回も統計量\(Z\)　と比べてみます。

確率変数（=棄却限界値）Kp = -1.645　＞　統計量\(Z\)= -1.8　ですので、統計量\(Z\)　は棄却域内にあると判断されます。

\[\]

よって、帰無仮説「母平均に対し、標本平均の変化がない：\(μ=\bar{x}\)」は棄却され、「平均値は小さくなった」　と判断されます。

\[\]

④両側検定と片側検定の総括

両側検定と片側検定をみてみましたが、ここで疑問が生まれましたよね？

同じ統計量\(Ｚ=-1.8\)なのに、両側検定では「平均値に変化なし」と判断したのに、片側検定では「平均値が小さくなった」と判断したのです。

なぜこのような結果になったのでしょうか？

(。´･ω･)?

\[\]

理由は「第一種の誤りを5%に固定して考えたから」です。

どういうことでしょうか？

　(。´◎ω◎)?

\[\]

両側検定では第一種の誤りを5%とすると、期待値付近（中心付近）の上位95%が採択域となりました。

しかし片側検定では、どちらかの大小関係のみに着目するため、逆の変化に対しては許容することになります。

\[\]

③の問題で考えてみると、「平均値は小さくなったか」という質問に対し、「平均値に変化はなかった」だけではなく「平均値は大きくなった」も採択域に入るのです。

両側検定の棄却域である「大きくなった2.5%分」が、「小さくなった2.5%分」に足されるのです。

このため、第一種の誤りを5%に固定している場合は、両側検定と片側検定では棄却限界値が変わってしまうのです。

\[\]

まとめ

①母分散が既知の場合の平均値の変化は、正規分布でみつもる

②両側検定では、棄却限界値は P=0.025　の時の確率変数になる

③片側検定では、棄却限界値は P=0.05　の時の確率変数になる

④両側検定と片側検定で棄却限界値が異なるのは、第一種の誤り(α)を固定しているため。　

\[\]

次回は「平均値に関する検定2」と称して、\(t\)検定について勉強してみましょう。

⇒オススメ書籍はこちら

⇒サイトマップ