ばらつきに関する検定1 :カイ二乗検定

公開日2020年5月6日 　最終更新日 2022年7月26日

みなさんこんにちは、michiです。

前回は平均値に関する検定1,2と称し、正規分布と\(t\)分布の検定を学びました。

今回はばらつきに関する検定1と称して\(χ^2\) (カイ二乗)検定について勉強します。

キーワード「\(χ^2\)カイ二乗検定」「\(χ^2\) (カイ二乗)表」「自由度」

①\(χ^2\)カイ二乗表を使った検定

母集団から標本を抽出し、そのばらつき（＝分散）を評価するには二つの統計量があります。

統計量\(χ^2\)カイ二乗と統計量\(F\)です。

使い分け方は

• 統計量\(χ^2\)カイ二乗は、母集団かの分散の変化を表す
• 統計\(F\)は、二つの母集団から得られた標本の分散の差異を表す

今回はばらつきの変化に着目するため、「\(χ^2\)分布から統計量を見積もる」方法を紹介します。

\[\]

②\(χ^2\)カイ二乗表のミカタ

いきなり問題を解く前に、\(t\)検定と同様に\(χ^2\)カイ二乗検定にも「\(χ^2\)カイ二乗表」というものがあります。

まずはその「\(χ^2\)カイ二乗表」のミカタを理解しましょう。下表

_(:3｣ ∠)_　　　見る気がしない・・・

基本的な見方は\(t\)表と同じで、自由度\(Φ\)と確率Pの重なるところを見ます。

\[\]

\(χ^2\)カイ二乗表は、\(t\)表に似ている点と似ていない点がありますね。

• 似ている点：確認Pと自由度\(Φ\)で確率変数が決まる
• 似ていない点：確認Pに95%以上の値（＞0.950）がある

似ている点の理解ですが、\(χ^2\)カイ二乗分布は\(t\)分布と同様に自由度で形の変わる分布関数です。

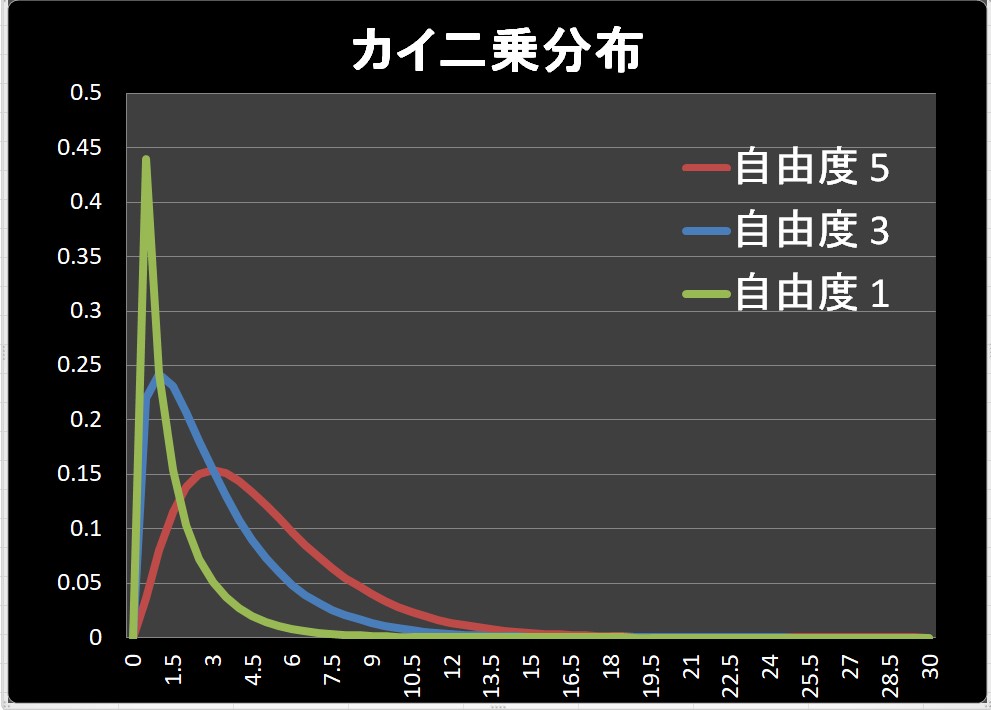
そのため、自由度によって棄却域と採択域が変わります。

\[\]

次に似ていない点の理解ですが、\(t\)表や正規分布表にはなかった、確認P=95%以上の値が書かれています。

なぜでしょうか？

(。´･ω･)?

\[\]

答えは「左右非対称」だからです。

左右対称な形の\(t\)分布や正規分布では、棄却限界値はプラス・マイナスの符号が異なるだけで、絶対値は同じでした。

そのため、その対称性から片側10％以下の棄却域が分かれば、反対側の“90%以上”の棄却域が分かりました。

\(χ^2\)カイ二乗分布はその非対称性から、両側検定で第一種の誤りが5%の場合は、右側2.5%と左側97.5%の確率の値を棄却限界値にすることになります。

\[\]

③両側検定の\(χ^2\)カイ二乗分布

\(χ^2\)カイ二乗表のミカタも分かったので、早速例題を解きながら勉強しましょう。

問）母平均\(μ\)=12 で母分散\(σ^2\)=2 の母集団からサンプルを11個抽出した。サンプルの標本平均\(\bar{x}\)=13.2　不偏分散は\(V\)=4 、平方和\(S\)=40 となった。

この時、ばらつきは変化したか、第一種の誤りを5%として答えてね。

\[\]

まずは、次の三つをチェックします。

• 平均の変化か、ばらつき（分散）の変化か
• 変化の有無か、大小関係か
• 母分散が既知か、不偏分散のみ既知か

今回の場合は「ばらつき（分散）の変化、変化の有無、母分散が既知」ですので、\(χ^2\)カイ二乗分布の統計量\(χ^2\)を使います。

\[\]

すると、

今回の帰無仮説は「母分散に対し、標本のばらつきに変化はない：\(σ^2 =2.0\)」で、対立仮説は「母分散に対し、標本のばらつきに変化がある：\(σ^2 ≠2.0\)」です。

統計量\(χ^2\) は、「 \(χ^2\)= 平方和 ÷ 母分散」　なので、

\[χ_0^2= \frac{40}{2} =20\]

※問題では平均値が与えられていますが、ばらつきの評価には不要なので、無視します。

\[\]

※今回は平方和の値が問題文から与えられていましたが、平方和が与えられていない場合は、

不偏分散(\(V\))×自由度(\(Φ\))=平方和(\(S\))　を求め、統計量\(χ_0^2\)を決めます。

\[\]

統計量\(χ_0^2\)の値が決まったので、棄却域を決めるために棄却限界値を求めます。

今回は両側検定になりますので、\(χ^2\)カイ二乗表より、

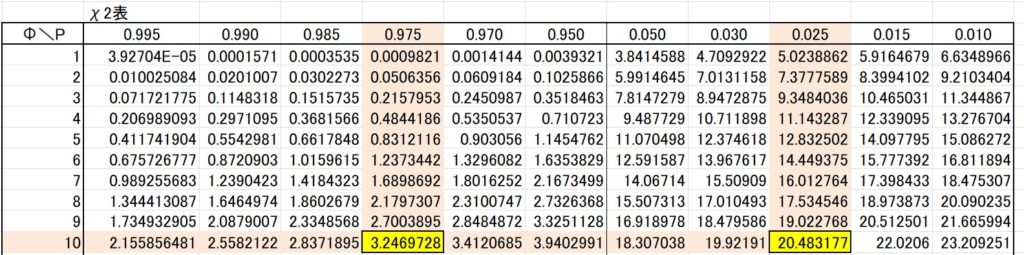
棄却限界値\(χ^2\)(10,0.025) = 20.4832　と　棄却限界値\(χ^2\)(10,0.975) = 3.2470　となります。

※棄却限界値の表し方は\(t\)表と同じで、\(χ^2\)(自由度、有意水準（＝第一種の誤り）/2)となります。

それでは検定統計量\(χ^2\)と比較してみましょう。

\[\]

「棄却限界値\(χ^2\)(10,0.025) = 20.4832　＞　統計量\(χ_0^2\) = 20 ＞ 棄却限界値\(χ^2\)(10,0.975) = 3.2470」　です。

統計量\(χ_0^2\)は採択域内にあると判断されます。

よって、帰無仮説「母分散に対し、標本のばらつきに変化はない：\(σ^2 =2.0\)」は採択され、「ばらつきに変化があるとは言えない」と判断します。

設問の両側検定のイメージ

\[\]

④片側検定の\(χ^2\)カイ二乗検定

では、次に質問を変えて片側検定をしてみます。

問）母平均\(μ\)=12 で母分散\(σ^2\)=2 の母集団からサンプルを11個抽出した。サンプルの標本平均\(\bar{x}\)=13.2　不偏分散は\(V\)=4 、平方和\(S\)=40 となった。

この時、標本のばらつきは大きくなったか、第一種の誤り5%として答えてね。

\[\]

先ほどの質問とパラメータは同じですが、問われている内容が変わりました。今回も三つのキーワードをチェックしてみます。

• 平均の変化か、ばらつき（分散）の変化か
• 変化の有無か、大小関係か
• 母分散が既知か、不偏分散のみ既知か

今回の場合は「ばらつき（分散）の変化、大小関係、母分散が既知」ですので、\(χ^2\)カイ二乗分布の統計量\(χ^2\)を使います。

さて、今回の帰無仮説は「母分散に対し、標本のばらつきに変化はない：\(σ^2 =2.0\)」で同じですが、対立仮説は「母分散に対し、標本のばらつきは大きくなった：\(σ^2\) ＞2.0」です。

\[\]

両側検定と片側検定では棄却域が変わります。結論からいうと、

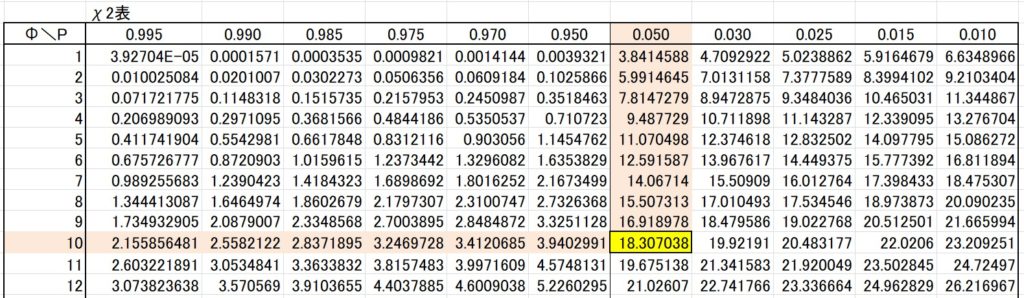
「棄却限界値\(χ^2\)(10,0.05) = 18.3070　＜　統計量\(χ_0^2\) = 20」となります。

統計量\(χ_0^2\) は棄却域内にあると判断できます。

\[\]

よって、帰無仮説の「母分散に対し、標本のばらつきに変化はない：\(σ^2 =2.0\)」は棄却され、対立仮説の「母分散に対し、標本のばらつきは大きくなった：\(σ^2\) ＞2.0」が採択されます。

つまり、「ばらつきは大きくなった」と判断します。

設問の片側検定のイメージ

※なぜ両側検定では「ばらつきに変化があるとは言えない」なのに、片側検定では「ばらつきが大きくなった」と違う結論になった理由は、記事「平均値に関する検定1 :正規分布」 をご参考ください

\[\]

⑤なぜ平方和を母分散でわるのか

さて、\(χ^2\)カイ二乗検定では、検定統計量\(χ_0^2\)を「平方和 ÷ 母分散」　で求めました。

なぜ　「不偏分散 ÷ 母分散」　ではダメなのでしょうか？　

母集団と標本の分散の比を求めるなら、それでもよさそうですよね？　

(。´･ω･)?

\[\]

理由は「自由度」によって棄却域が変わるからです。

記事「カイ二乗分布とは」に、以下の記述をしました。

＊＊＊＊＊＊

自由度は定数になるので今回は無視して考える（検定で説明します）と、カイ二乗分布は母標準偏差と、標本の標準偏差の比を評価しているだけのようです。

つまり、カイ二乗分布は母集団の「ばらつき」と標本の「ばらつき」の違いを評価することに使われます。

＊＊＊＊＊＊

この時は\(χ^2\)カイ二乗分布のイメージをしやすくするために、自由度を無視して考えてもらいました。

ところが、検定では棄却限界値を知ることが重要になります。

\(χ^2\)カイ二乗分布は自由度によって形の変わる分布なので、「不偏分散 ÷ 母分散」の値に変化がなくても、自由度によってその統計量は棄却域に入ったり入らなかったりします。

\[\]

そのため、統計量\(χ^2\)　は、自由度を考慮した平方和（＝不偏分散×自由度）を母分散でわるのです。

\[\]

まとめ

①分散の変化を検定したい場合は、\(χ^2\)検定

②\(χ^2\)カイ二乗表のミカタは\(t\)表と同じで、自由度と確率で確率変数を求める

③両側検定の棄却限界値は、左右非対称なので値の絶対値が異なる

④片側検定の棄却限界値は、\(χ^2\)カイ二乗表をそのまま読めばよい

⑤検定統計量\(χ^2\)は「平方和 ÷ 母分散」　平方和を使う理由は自由度のせい

\[\]

今回は\(χ^2\)検定について勉強しました。

次回は\(F\)検定について勉強していきましょう！

\[\]

⇒オススメ書籍はこちら

⇒サイトマップ