ワイブル分布 とは

公開日2021年10月7日 最終更新日 2021年10月31日
みなさんこんにちは、michiです。
今回はワイブル分布について勉強します。
ワイブル分布はテキストでは後半にでてきますが、実用面でかなり使えるので、早めに紹介します。
エクセルを使った実践的な計算方法は、実践編で紹介します。
キーワード:「位置パラメータ」「形状パラメータ」「尺度パラメータ」
目次
①ワイブル分布とは
ワイブル分布とは故障の分布(寿命)を表す密度関数のことです。
ワイブル分布は以下の式で表せます。
\[f(t)=\left( \frac{m}{\eta}\right) \left(\frac{t-\gamma}{\eta}\right)^{m-1} exp\left\{-\left(\frac{t-\gamma}{\eta}\right)^m\right\}\]
- \(\gamma\):位置パラメータ
- \(m\):形状パラメータ
- \(\eta\):尺度パラメータ
- \(t\):時間や回数など、寿命を表すパラメータ
\[\]
位置パラメータ\(\gamma\) によって分布の始まりが、形状パラメータ\(m\)によって分布の形が、尺度パラメータ\(\eta\)によって分布の広がりが決まります。
具体的なイメージは、下の図1~図3を参考にしてください。

\[\]

\[\]

なんとなくイメージができましたか?
(A;´・ω・)アセアセ
\[\]
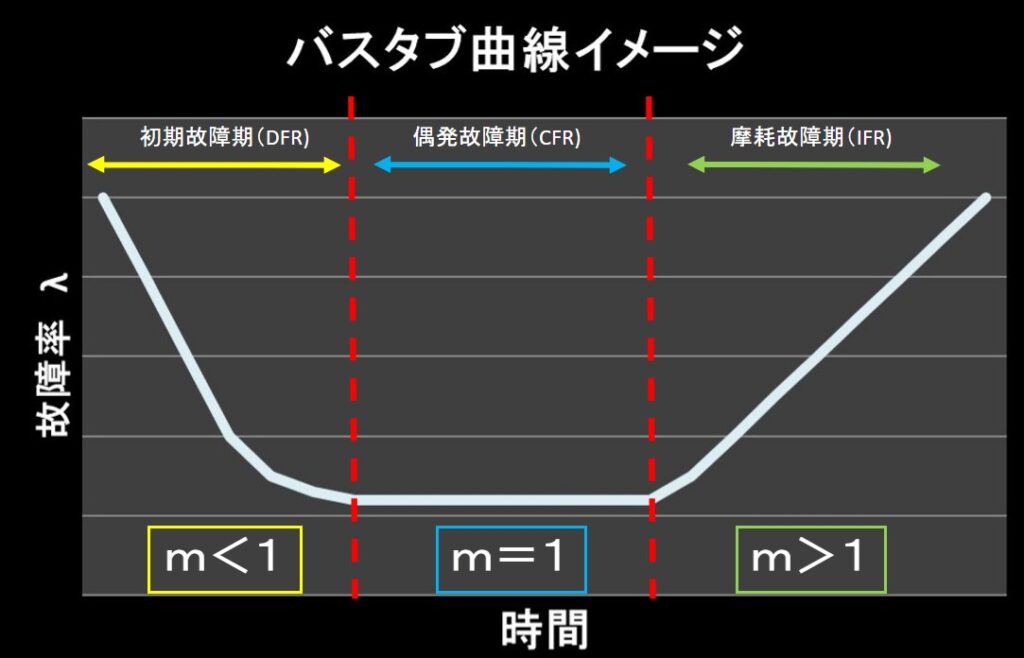
形状パラメータ\(m\)によってどの故障期間の分布かが決まります。
- \(m<1\):初期故障型
- \(m=1\):偶発故障型
- \(m>1\):摩耗故障型
故障期間の説明については、記事「信頼性工学1」のバスタブ曲線をご参照ください。
形状パラメータとバスタブ曲線の関係をまとめると、次のイメージになります。
\[\]
ワイブル分布では、故障期間にかかわらず形状パラメータ\(m\) として表せます。
こんなに便利なワイブル分布ですが、弱点があります。
それは、「各パラメータを直接求めることができない」ということです。
Σ(・ω・ノ)ノ!
ではどうすればいいのか?というと、「ワイブル分布確率変紙」を使います。
\[\]
②ワイブル分布確率紙とは
ワイブル分布確率紙とは、ワイブル分布の三つのパラメータである、位置パラメータ\(\gamma\)、形状パラメータ\(m\)、尺度パラメータ\(\eta\) を求めるための表です。
一昔前まではその名の通り「紙」を使っていましたが、今はExcelで簡単にパラメータを求められます。
ワイブル分布確率紙は下のような表です。

※イメージ図:実際はもっとややこしいです。
\[\]
ワイブル分布確率紙では、横軸に\(t\)(下)と\(X=lnt\)(上)が、縦軸に\(F(t)\)(左)と\(Y=lnln\frac{1}{1-F(t)}\) (右)があります。
(o´・ω・)´-ω-)ウン
さて、今までの説明で出てきていないものがあります。
\(F(t)\) です。
\(F(t)\) は累積故障確率で、次の式で表されます。
\[F(t)=1-exp\left\{-\left(\frac{t-\gamma}{\eta}\right)^m\right\}\]
\(F(t)\) は不信頼度とも言われます。
\[\]
この累積故障確率\(F(t)\) を微分すると、先ほどのワイブル分布の式になります。
\[F(t)=1-exp\left\{-\left(\frac{t-\gamma}{\eta}\right)^m\right\}\]
\[↓微分↓\]
\[f(t)=\left( \frac{m}{\eta}\right) \left(\frac{t-\gamma}{\eta}\right)^{m-1} exp\left\{-\left(\frac{t-\gamma}{\eta}\right)^m\right\}\]
\[\]
ワイブル分布の形状を決める三つのパラメータを決めるには、累積故障確率\(F(t)\) を使います。
しかし、累積故障確率\(F(t)\)もなかなか複雑な式です。
(゜゜(。。(゜゜(。。 ウンウン
そこで、累積故障確率\(F(t)\)をわかりやすく計算するために、ワイブル分布確率紙を使います。
\[\]
ワイブル分布確率紙を使う前に、説明の便宜上まずは位置パラメータ\(\gamma\) を0と考えます。
すると、累積故障確率\(F(t)\)は次のようになります。
\[F(t)=1-exp\left\{-\left(\frac{t}{\eta}\right)^m\right\}\]
それでは、ワイブル分布確率紙の横軸 \(X=lnt\)、縦軸 \(Y=lnln\frac{1}{1-F(t)}\) を導いていきましょう。
\[\]
\[累積故障確率 F(t)=1-exp\left\{-\left(\frac{t}{\eta}\right)^m\right\}\]
\[1-F(t)=exp\left\{-\left(\frac{t}{\eta}\right)^m\right\}\]
両辺に対数をとって
\[ln(1-F(t))=-\left(\frac{t}{\eta}\right)^m\]
両辺に -1 をかけて
\[ln(1-F(t))^{-1}=\left(\frac{t}{\eta}\right)^m\]
\[ln\frac{1}{1-F(t)}=\left(\frac{t}{\eta}\right)^m\]
両辺にさらに対数をとって
\[lnln\frac{1}{1-F(t)}=mlnt – mln\eta\]
ここで、\(X=lnt\)、\(Y=lnln\frac{1}{1-F(t)}\) とすると、
\[Y=mX-mln\eta\]
形状パラメータ\(m\)、尺度パラメータ\(\eta\) は定数なので、\(Y=mX-mln\eta\) は一次関数(比例の式)になります。
\[\]
このように、ワイブル分布確率紙とは累積故障確率\(F(t)\) を一次関数に変換し、各パラメータを求めるツールになります。
\[\]
③ワイブル分布確率紙の使い方
ワイブル分布確率紙を使って三つのパラメータを求める手順は以下の通りです。
- プロットする方法を決める
- プロットした点を通るような直線を引く
- 形状パラメータ\(m\) を求める
- 位置パラメータ\(\gamma\) を求める
- 尺度パラメータ\(\eta\) を求める
\[\]
①プロットする方法を決める
ワイブル分布確率紙には、実際に故障に至った時間や回数をプロットします。
プロットをする際に、プロット位置を決める方法に「a)平均ランク法」と「b)メジアンランク法」があります。
どちらも縦軸に相当する\(i\)番目の故障データの累積故障頻度\(F(t(i))\) を求めます。
\[\]
a) 平均ランク法
\[F(t(i))=\frac{i}{n+1}×100(\%)\]
b)メジアンランク法
\[F(t(i))=\frac{i-0.3}{n+0.4}×100(\%)\]
またはメジアンランク表を使います。
\[\]
実用的には、 \(n\) 数が30個以下の場合はメジアンランク法が使われます。
実際に計算してみます。
例えば、\(n=10\) で\(i=3\) (3番目のデータ)をメジアンランク法で計算すると、
\[F(t(3))=\frac{3-0.3}{10+0.4}=25.96…\%\]
この計算を\(i=1\)から\(i=10\)まで10個分の故障の累積頻度\(F(t(i))\) を、横軸を壊れた順番にプロットしていきます。


\[\]

\[\]
②プロットした点を通るような直線を引く
「①プロットする方法を決める」でプロットした点を通るような直線を引きます。
直線を引くときには、つぎの3パターンに気をつけてください。
- a)直線が引ける
- b)直線が途中で折れる
- c)直線ではなく、曲線が引ける
\[\]
「a)直線が引ける」場合、そのまま次のステップ③へ進みます。
「b)直線が途中で折れる」場合、二つ(以上)の故障モードが混在している可能性があります。
二つ(以上)の故障モードに層別して、それぞれの故障モード毎にパラメータを決めていきましょう。
「c)直線ではなく、曲線が引ける」場合、適当な位置パラメータ\(\gamma\) を設定し、プロットした点が直線上に並ぶように調整します。
位置パラメータ\(\gamma\) の意味は、ある時間(回数)まではその製品は壊れないということです。
位置パラメータ\(\gamma\)を設定し、プロットした点が直線上に並んだら、次のステップへ進みます。

\[\]

\[\]

\[\]
③形状パラメータ\(m\) を求める
「②プロットした点を通るような直線を引く」で引いた直線を、\(X=lnt=1 \qquad Y=lnln\frac{1}{1-F(t)}=0\) を通るように平行移動します。

つぎに、\(X=lnt=0\) の時の\(Y\) の値を読み取ります。
この時の\(Y\) の値に(-)マイナスをかけた値が、形状パラメータ\(m\) となります。

\[\]
では、なぜこの方法で形状パラメータ\(m\) が求められるのでしょうか?
ワイブル分布確率紙では、累積故障率\(F(t)=1-exp\left\{-\left(\frac{t}{\eta}\right)^m\right\}\) を \(Y=mX-mln\eta\) と変形しました。
\(-mln\eta\) は定数なので、形状パラメータ\(m\) は横軸\(X\)、縦軸\(Y\)の 一次関数の傾きになります。
先ほどの図を一部拡大してみます。

横軸\(X=1\) の幅で縦軸\(Y\) の高さ、すなわち傾きを求めていることがわかります。
ただし、\(Y\) はマイナス方向の高さなので、読み取った形状パラメータ\(m\) にマイナスをかけます。
\[\]
④位置パラメータ\(\gamma\) を求める
位置パラメータ\(\gamma\) を求める場合は、プロットした点が曲線上に並ぶ場合です。
プロットする位置\(t\) を\(t’=t-\gamma\) としてプロットする位置(横軸)を変えます。
適当な\(\gamma\) を代入し、プロットした点が直線上に並べば、それが位置パラメータ\(\gamma\) になります。

上の図を見ると、\(\gamma\) で表される移動量が点によって異なって見えます。
ところが実際は、同じ移動量であることに気をつけてください。
※ワイブル分布確率紙は対数グラフのため、一見すると移動量が異なっているように見えます。
\[\]
なお、プロットした点が最初から直線上にある場合、その製品の位置パラメータ\(\gamma\) は 0 となります。
位置パラメータ\(\gamma\) が 0 の意味するところは、「使い始めたら壊れ始める」です。
\[\]
⑤尺度パラメータ\(\eta\) を求める
最後に尺度パラメータ\(\eta\) を求めます。
「②プロットした点を通るような直線を引く」で引いた直線と\(Y=0\) の交点の\(t\) を読みます。
※平行移動する前の直線です。

これが尺度パラメータ\(\eta\) です。
なぜ、この方法で尺度パラメータ\(\eta\) が求められるのでしょうか?
(。´・ω・)?
\[\]
式 \(Y=mX-mln\eta\) に \(Y=0\) を代入します。
すると、
\[Y=mX-mln\eta\]
\[0=mX-mln\eta\]
\[mX=mln\eta\]
ここで\(X=lnt\) なので、
\[mlnt=mln\eta ⇒ t=\eta\]
となります。
\(t\) は横軸の下側の値です。
以上で三つのパラメータを求める方法がわかりました。
\[\]
この記事だけでは、実践には心もとないですよね。
そこで、実践編でExcelを使ったワイブル分布解析方法を紹介します。
記事「【実践 6】Excelでワイブル分布の作り方」にまとめますので、読んでみてください。
\[\]
④オススメ書籍の紹介
今回はワイブル分布について紹介してきました。
今回の記事の参考図書を紹介します。↓
少し古い本なので、今の時代では「大丈夫?」って表現があります。
とはいえ、勉強には最適の本なので、ぜひ読んでみてください。
\[\]
⑤まとめ
①ワイブル分布は故障の分布を表す密度関数のこと
②ワイブル分布確率紙とは、ワイブル分布の三つのパラメータを求めるための表
③ワイブル分布確率紙の使い方
- プロットする方法を決める
- プロットした点を通るような直線を引く
- 形状パラメータ\(m\) を求める
- 位置パラメータ\(\gamma\) を求める
- 尺度パラメータ\(\eta\) を求める
④オススメ書籍、買ってみてね!
\[\]
今回はワイブル分布について学びました。
QC検定1級ではあまり出現頻度の高くない内容です。
しかし、実務では製品の寿命を見積もる際に非常に有効になります。
ぜひ実践で活かしてみてください!
\[\]
















[…] ワイブル分布の詳細は、記事「ワイブル分布 とは」をご参照ください。 […]
非常にわかりやかったです!
ありがとうございます♪