平方和の式の暗記法

公開日2020年1月25日 最終更新日 2022年4月5日
みなさんこんにちは michiです。
QC検定や統計の勉強をすると、平方和の式が覚えづらいと感じることはありませんか?
そこでおぼえやすい語呂合わせを考えました!
この記事では、平方和の暗記法と平方和の意味を説明していきます。
キーワード:「平方和」「ばらつき」
目次
①平方和の覚え方
「庭にひくサンプル分のワニ」
おぼえにくいですかね?下のようなイメージです。

語呂だけ覚えても意味ないですよね、おぼえる数式は下の式になります。
\[ \sum x_i^2 - \frac{(\sum x_i)^2}{n}\]
\[ x_i の i はデータ数, nはサンプル数\]
最初の項でサンプル値各々の「二乗の和」を計算し、そこからサンプル値の「(全体の)和の二乗」をサンプル数で割った値で引き算します。
この計算で、ややこしい平方和の計算が楽になります。
「庭にひくサンプル分のワニ!」
\[\]
②計算例
下の表 1段目は 6個のデータ(データA から データF )の値が、それぞれ 1から 6であることを表します。
2段目は6個のデータそれぞれを 2乗した結果とその合計(和)です。
| データA | データB | データC | データD | データE | データF | 合計(和) | |
| \[x_i\] | 1 | 2 | 3 | 4 | 5 | 6 | 21 |
| \[x_i^2\] | 1 | 4 | 9 | 16 | 25 | 36 | 91 |
これを先ほど覚えた「庭にひくサンプル分のワニ」を使うと、
\[ 平方和 (S) = 91 - \frac{21 \times 21}{6} = 17.5\]
上の例では、「庭」 が「二乗の和 = 91」、「にひく」が「- マイナス」、「サンプル分」が 「データの数 = 6 (分母)」、「ワニ」が「和の二乗 = 21 × 21」 を表します。
\[\]
一見すると複雑な計算に見えますが、平方和の定義から計算するよりは楽な場合が多いです。
\[\]
③平方和 とは?
いきなり平方和の式の暗記方法と実例をあげましたが、そもそも平方和とは何で、何のために計算するのでしょうか?
本来、「平方和の定義」は以下の式で計算されます。
\[ 平方和 (S) = \sum (x_i – \overline{x})^2 \]
\[ \overline{x} は x の平均値を表します。\]
この式の意味は、「各測定値 - 測定値の平均 の 2乗 の合計」です。
つまり、平方和は「平均からのずれの合計」を表すため、データ全体の「ばらつき」を評価するときに有効です。
\[\]
では、なぜずれを評価するために 二乗するのでしょうか?
それは、 「マイナス をださないため」 です。
(。´・ω・)?
先ほどの例で、平均値からのずれの合計を二乗しないで、ばらつきとして評価してみましょう。
平均値が3.5ですので、
\[ (1 – 3.5) + (2 – 3.5) + (3 – 3.5) + (4 – 3.5) + (5 – 3.5) + (6 – 3.5)\]
\[(-2.5)+(-1.5)+(-0.5)+0.5+1.5+2.5 \qquad = 0\]
このように、プラスマイナスが打ち消しあって0となってしまいます。
これでは、データごとのばらつきが評価できません!
┐(´д`)┌
\[\]
では、「平方和の定義」に従って先ほどの計算をしてみましょう。
\[ (1 – 3.5)^2 + (2 – 3.5)^2 + (3 – 3.5)^2 + (4 – 3.5)^2 + (5 – 3.5)^2 + (6 – 3.5)^2=\]
\[= 6.25 + 2.25 + 0.25 + 0.25 + 2.25 + 6.25 = 17.5 \]
0にはなりませんね。
先ほどと同じ計算結果になりました。(っほ。
\[\]
エクセルなどの計算ソフトを使う場合は別として、QC検定試験ではこの計算は時間もかかり、ミスも増えそうです。
平方和の計算では、「庭にひくサンプル分のワニ」を利用してみてください。

\[\]
④なぜ「庭にひくサンプル分のワニ」になるのか?
計算式「庭にひくサンプル分のワニ」を証明します。
\[ 平方和 (S) = \sum (x_i – \overline{x})^2 \]
\[= \sum(x_i^2 - 2 \times x_i \times\ \overline{x} + \overline{x}^2) \]
ここで、平均値は測定値の合計をサンプル数でわった値なので、
\[\overline{x} = \frac{\sum x_i}{n} \]
また、平均値のΣ(シグマ:先ほどの例では、サンプル数6)は、合計値=平均値 × サンプル数 を意味するので、
\[\sum \overline{x} = n \times \overline{x} \]
よって、計算をすすめると
\[= \sum x_i^2 - 2 \times \sum x_i \times (\frac{\sum x_i}{n}) + n \times(\frac{\sum x_i}{n})^2 \]
\[ =\sum x_i^2 - 2 \times \frac{(\sum x_i)^2}{n} + \frac{(\sum x_i)^2}{n} \]
\[= \sum x_i^2 - \frac{(\sum x_i)^2}{n}\]
なるほど!Σ(・ω・ノ)ノ!
納得していただけたでしょうか?
\[\]
⑤平方和じゃない!? SUMSQ関数とは
平方和の計算はデータが増えてくると、計算が面倒です。
そこでエクセル関数を使って計算してみましょう。
\[\]
google先生によると、「SUMSQ関数」で平方和が計算できるようです。
φ(・ω・ )フムフム…
\[\]
ではここで問題です。
問)次の数字の集団の平方和を計算しましょう
\[{8,9,10,11,12}\]
\[\]
「庭にひくサンプル分のワニ」で計算すると、
二乗和は
\[8^2+9^2+10^2+11^2+12^2 = 510\]
和の二乗は
\[(8+9+10+11+12)^2=2500\]
サンプル数が 5 なので、 「庭にひくサンプル分のワニ」 は
\[510-\frac{2500}{5}=10\]
\[\]
計算できました!
ところで、今回の問題だと「③平方和とは?」に書いた定義から計算する方法が早いです。
平均値は 10 なので
\[(8-10)^2+ (9-10)^2+ (10-10)^2+ (11-10)^2+ (12-10)^2 \]
\[=4+1+0+1+4=10\]
\[\]
それでは、エクセル関数「SUMSQ関数」の出力結果を確認しましょう。
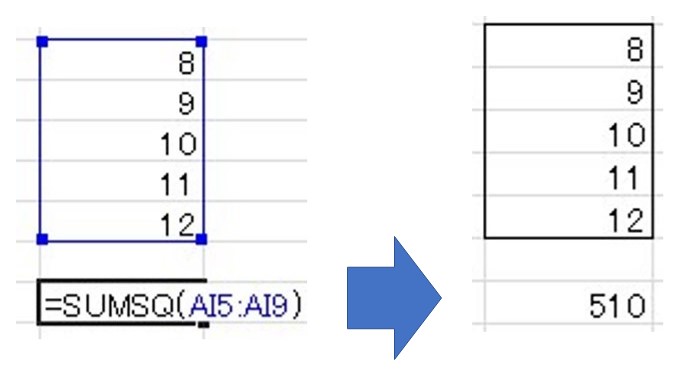
Σ(・ω・ノ)ノ!
いやはや、 10 になりません!
\[\]
理由は、Excel関数「SUMSQ関数」では、「平方の和」を計算しているからです。
平方とは二乗という意味です。
その和なので、 「平方の和」 となるわけです。
計算は
\[8^2+9^2+10^2+11^2+12^2 = 510\]
です。
\[\]
つまり 「SUMSQ関数」では、 「平均値と各値の差分の平方の和(=平方和)」を計算しているのではなく、「各値の平方の和」を計算しているのです。
これは注意が必要ですね!
( •̀ω •́ゞ)✧ラジャ
\[\]
まとめ
①平方和の暗記法は「庭にひくサンプル分のワニ」
②計算例といてみた
③平方和は、測定値と平均値のずれ の二乗 の合計値
④なぜ「庭にひくサンプル分のワニ」になるのか、証明してみた
⑤ エクセル関数「SUMSQ関数」では「平方の和」を計算している
\[\]
次回の記事では「平方和」と「不偏分散」について学びましょう!














[…] なぜ二乗するのかについては、記事「平方和の式の暗記法」をご参照ください。 […]
[…] 記事「平方和の式の暗記法」で紹介した、「庭にひくサンプル分のワニ」の「サンプル分のワニ」に該当する部分を計算します。 […]
[…] この公式の覚え方は、「庭にひくサンプル分のワニ」です。 […]
[…] 平方和の計算式「庭にひくサンプル分のワニ」に似ていますよね。 […]
[…] 「平方和の式の暗記法」 […]
[…] 平方和の詳細は記事「平方和の式の暗記法」をご参照ください。 […]
[…] ※「平方和の式の暗記法」で覚えた語呂「庭にひくサンプル分のワニ」と比較すると「サンプル分の」がなくなっています。これは母分散を考えているためです・・・ […]
私が購入した参考書(3級)では平方和の定義から「庭にひくサンプル分のワニ」に行くまでの途中式がかなり省かれており、何故この定義からこの式が導き出されるのか分からず、暗記に頼るしかないのかと諦めかけていましたが、michiさんのブログを拝見し、とても丁寧に途中式が説明されていましたので助かりました。ありがとうございます。
参考になったようで幸いです。
式の導出を丁寧に説明する参考書は少ないかもしれません。
QC検定3級用の自作の問題を30問記事に載せていますので、そちらも参考にしてみてください。
[…] 詳細は、記事「平方和の式の暗記法」をご参考ください。 […]
[…] 平方和 (S) の計算式 […]
[…] 平方和 (S) の計算式 […]