カイ二乗分布とは

公開日2020年4月27日 最終更新日 2022年6月12日
みなさんこんにちは、michiです。
前回の記事では母集団と標本の違いについて勉強しました。
今回は \(χ^2\)分布(カイ二乗分布)について勉強していきましょう!
キーワード「\(χ^2\) カイ二乗分布」
目次
①\(χ^2\) カイ二乗分布とは?
いままでの記事で、正規分布、二項分布、ポアソン分布、について勉強してきました。
今回勉強する \(χ^2\) カイ二乗分布は「標準正規分布を基にした確率分布(検定統計量)」になります。
\[\]
具体的な式は以下の通りです。
\[χ^2=Z_1^2+Z_2^2+・・・+Z_n^2\]
この式で表される確率分布を 「自由度\(n-1\) の\(χ^2\)分布(カイ二乗分布)」と言います。
※データ数が\(n\) なので、自由度は\(n-1\) となります。
“φ(・ω・。)フムフム…
\[\]
このとき、統計量\(Z\)は標準化した統計量で、 \(Z=\frac{x-μ}{σ}\) (\(x\):測定値、\(μ\):母平均、\(σ\):母標準偏差)です。
これをグラフで書くと、以下のようになります。
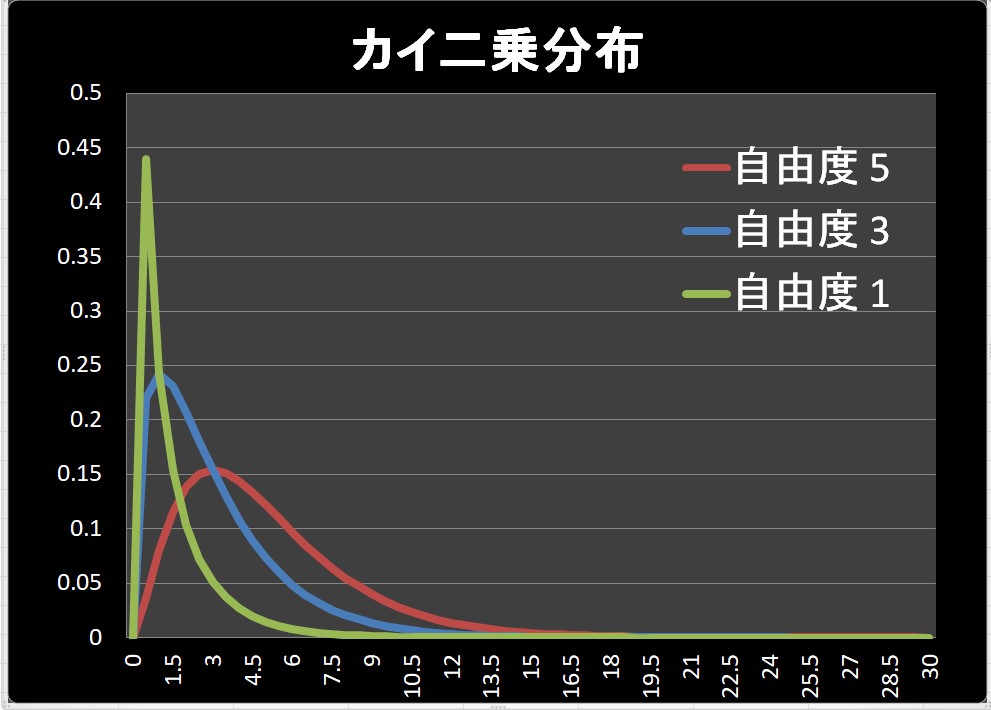
正規分布に比べると、だいぶ見た目が変わっていますね。
このグラフからわかる特徴について考えてみましょう。
\[\]
②なぜ左右非対称なのか
正規分布では、母平均(標準正規分布では 0 )を中心に左右対称につりがね型の分布をしていました。
カイ二乗分布のグラフをみて、「左右非対称」ということに気づきます。
なぜ左右非対称になるのでしょうか?
(。´・ω・)?
\[\]
カイ二乗分布の式を変形させてみると、
\[χ^2=Z_1^2+Z_2^2+・・・+Z_n^2\]
\[=(\frac{x_1-μ}{σ})^2+(\frac{x_2-μ}{σ})^2+・・・+(\frac{x_n-μ}{σ})^2\]
カイ二乗分布では、測定値と母平均との差を二乗しているために、マイナスの値はなくなります。
さらに、二乗の和の合計が\(χ^2\)カイ二乗分布となるので、左右非対称の形になってしまうのです。
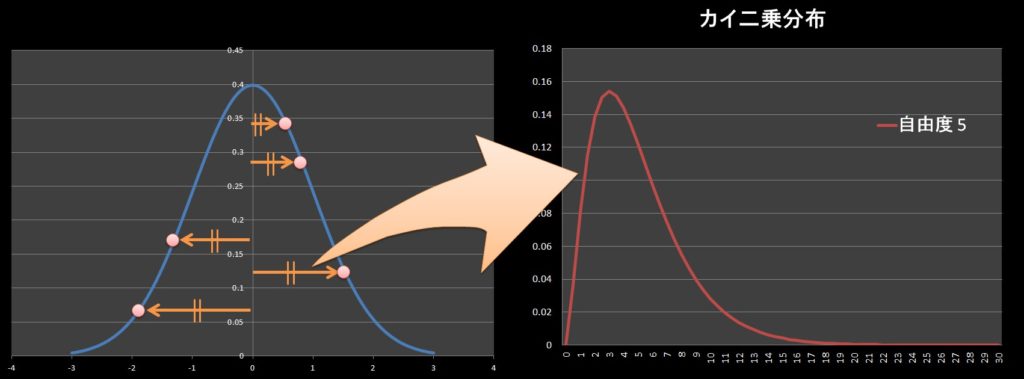
※上のイメージ図では、標準正規分布の中心(= 0)から、測定値との差を二乗したものを5点分(自由度 5 の場合)を足した確率分布をプロットしています。

\[\]
③なぜ自由度によって形が変わるのか?
さて、カイ二乗分布の特徴は左右非対称というだけではありません。
「自由度によって形がかわる」というのもその特徴です。
\[\]
カイ二乗分布は統計量\(Z\)の二乗の和です。
\(Z^2\)は「マイナス」にならないので、測定数\(n\) が増えれば、必然的にカイ二乗の値も増えます。
\[\]
ここでのポイントは、統計量\(Z\)は「標準化された統計量」ということです。
標準化とは、「正規分布のミカタ」の記事より
\[平均値(期待値)=0、分散=1^2 \]
の分布です。
つまり、標準化によって、元のデータの平均や標準偏差が何であろうと、同じ方法で統計量を評価できることを示唆してます。

\[\]
④実用的には 「平方和÷母分散」
カイ二乗分布について何となくわかってきました。
実用的にはどう使えばよいのでしょうか?
(。´・ω・)?
\[\]
カイ二乗分布の定義式をもう少し変形させてみましょう。
\[χ^2=Z_1^2+Z_2^2+・・・+Z_n^2\]
\[=(\frac{x_1-μ}{σ})^2+(\frac{x_2-μ}{σ})^2+・・・+(\frac{x_n-μ}{σ})^2\]
\[=\frac{1}{σ^2}((x_1-μ)^2+(x_2-μ)^2+・・・+(x_n-μ)^2)\]
\[=\frac{1}{σ^2}\sum (x_i – μ)^2\]
\(\frac{1}{σ^2}\) を無視すると、見覚えのある形が出てきました。これは・・・
「平方和」の定義ですよね。
(´・ω・`)モキュ?
\[\]
詳細は、記事「平方和の式の暗記法」をご参考ください。
つまり、カイ二乗分布は、
\[χ^2=\frac{S}{σ^2}=\frac{平方和}{母標準偏差^2(=母分散)}\]
ということになります。
Σ(・ω・ノ)ノ!

\[\]
⑤なぜ\(χ^2\) カイ二乗分布を使うのか
カイ二乗分布の統計量が「平方和」と「母標準偏差\(^2\)」で表されることがわかりました。
平方和も母標準偏差も「ばらつき」を評価するものでした。
つまり、カイ二乗分布は評価したい集団の「ばらつき」の評価に使います。
\[\]
ここで一つの疑問が生じます。
「なぜわざわざ平方和を母標準偏差で割ったものを使うのか?」です。
・・・(。´・ω・)?
\[\]
この疑問に答えるために、カイ二乗分布の式をもう少し変形させてみます。
\[χ^2=\frac{S}{σ^2}=\frac{ΦV}{σ^2}\]
\[=Φ\frac{s^2}{σ^2}=自由度 × \frac{標本の標準偏差^2(=不偏分散)}{母標準偏差^2(=母分散)}\]

自由度は定数になるので今回は無視して考える(検定で説明します)と、カイ二乗分布は母標準偏差と、標本の標準偏差の比を評価しているだけのようです。
つまり、カイ二乗分布は母集団の「ばらつき」と標本の「ばらつき」の違いを評価するために使われているのです。
\[\]
⑥例題
説明が続いたので、例題を一問といてみましょう。
問)母標準偏差 0.3 の正規分布をする母集団から、サンプルを13個取り出したときのサンプルの平均値は 6.7、平方和は 4.05 であった。この時のカイ二乗統計量をもとめよ。
答)
\[χ^2=\frac{平方和}{母標準偏差^2}=\frac{4.05}{0.3^2}\]
\[=45\]
この問題のポイントは
- サンプル数に惑わされない
- サンプルの平均値に惑わされない
カイ二乗の統計量を計算するには、標本の平方和と母標準偏差がわかればOKです。
\[\]
まとめ
①\(χ^2\)カイ二乗分布は、\(χ^2=Z_1^2+Z_2^2+・・・+Z_n^2\)
②\(χ^2\)カイ二乗分布は、左右非対称な分布関数
③\(χ^2\)カイ二乗分布は、自由度(サンプル数)によって形が変化
④\(χ^2\)カイ二乗分布は、\(χ^2=\frac{平方和}{母標準偏差^2(=母分散)}\)
⑤\(χ^2\)カイ二乗分布は母集団の「ばらつき」と標本の「ばらつき」の違いを評価
⑥標本の平方和と母標準偏差がわかれば、統計量を計算できる。
\[\]
今回は\(χ^2\)カイ二乗分布とは何かについて勉強しました。
\(χ^2\)カイ二乗分布を使った検定や推定の方法については、またの機会にまとめます。
次回はF分布について勉強していきましょう!














[…] 記事「カイ二乗分布とは」に、以下の記述をしました。 […]
[…] 前回勉強した(χ^2)カイ二乗分布では、母分散と標本の分散のばらつきを評価していました。 […]