分散に関する推定

公開日2020年5月18日 最終更新日 2021年9月20日
みなさん、こんにちはmichiです。
前回は平均値に関して区間推定をしました。
今回は標準偏差の推定について学んでいきましょう。
キーワード:「\(χ^2\)カイ二乗分布」「平方和」「母分散」
目次
①母標準偏差/母分散の点推定
前回の平均値に関する推定の記事で、推定には以下の二種類があることを学びました。
- 点推定とは、標本から得られたデータでただ一つの値を求めること
- 区間推定とは、母集団の真の値が任意の確率であてはまる範囲を求めること
平均値ではなくデータの「ばらつき」を推定したい場合は、標準偏差や不偏分散を使って、点推定や区間推定を行います。
また、ばらつきの点推定では、母分散≒不偏分散 と考えます。

\[\]
②母標準偏差/母分散の区間推定
標準偏差の区間推定は、平均値の区間推定と同様の考え方をします。
検定統計量\(χ^2\)(カイ二乗)が採択域内に入る範囲を求めます。
\[χ^2 = \frac{S}{σ^2}= \frac{平方和}{母分散}\]
\[\]
ここで、困ったことになります。
検定統計量\(χ^2\)を使おうにも、母分散\(σ^2\)の値が分からないので求められません。
(゚-゚;)コマッタ
\[\]
というより、母分散\(σ^2\)の信頼区間を求めようとしているので・・・
先ほどの式を以下のように変形します。
\[σ^2 = \frac{S}{χ^2}= \frac{平方和}{カイ二乗}\]
\[\]
ここで、\(χ^2\)カイ二乗分布について少しおさらいをします。
\(χ^2\)カイ二乗分布は下図のような形をしていました。
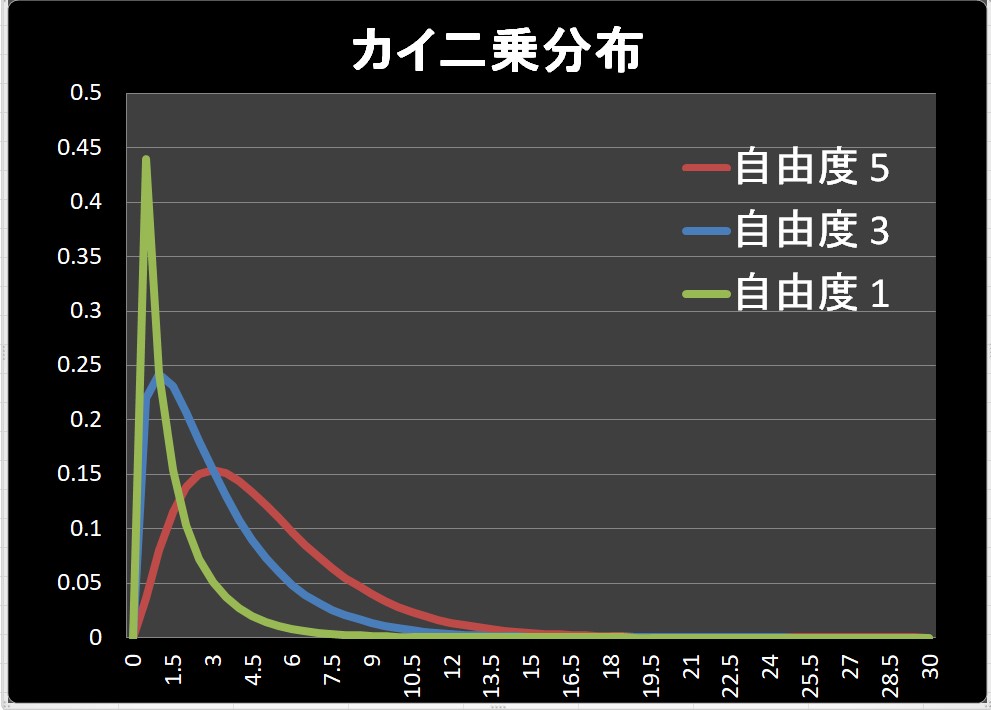
特徴は
- 自由度で形が変わる
- 左右非対称な形(正規分布やt分布と異なる)
正規分布や\(t\)分布は左右対称な形のため、平均値の区間推定はそれぞれ以下の式で求められました。
\[\bar{x}±Z(\frac{α}{2})×\frac{σ}{\sqrt{n}} ,\qquad \bar{x}±t(Φ,α)×\sqrt{\frac{V}{n}}\]
つまり標本平均である\(\bar{x}\) に対して同じ値を±して区間推定していました。
\[\]
左右非対称な形の\(χ^2\)カイ二乗分布では、母分散の信頼区間は以下の式になります。
\[\frac{S}{χ^2(Φ,\frac{α}{2})} ≦ σ^2 ≦ \frac{S}{χ^2(Φ,1-\frac{α}{2})}\]
これを図示すると下図になります。

この時、標本平均\(\bar{x}\)から信頼区間の上限と下限までの差は異なります。
\[\]
③統計量\(χ^2\)カイ二乗の上限と下限設定
先ほどの図をよく見ると、疑問が生まれます。
左側の棄却限界値が、\(χ^2(Φ,1-\frac{α}{2})\)なのに、母分散の信頼区間の上限になっています。
(。´・ω・)?
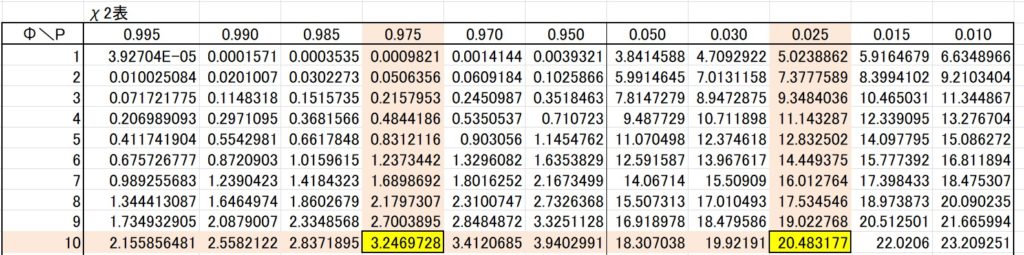
\(χ^2\)表を見ると、同じ自由度(例えば10)では、\(χ^2(10,0.975)\)=3.24697 で、\(χ^2(10,0.025)\)=20.4832 ですから、
\(χ^2(10,0.975) < χ^2(10,0.025)\) です。
\[\]
もう一度母分散の信頼区間の式をよく見ると・・・
\[\frac{S}{χ^2(Φ,\frac{α}{2})} ≦ σ^2 ≦ \frac{S}{χ^2(Φ,1-\frac{α}{2})}\]
\[\]
\(χ^2\)カイ二乗の値は分母にあります。
信頼区間を推定する場合の平方和\(S\)は同じ値ですから、分母が大きいほど全体の値は小さくなります。
そのため、信頼区間は先ほどの式で表されるのです。
\[\]
なお、母分散の上限が \(\frac{S}{χ^2(Φ,1-\frac{α}{2})}\) と、確率が\(1-\frac{α}{2}\)になる理由は、
記事「ばらつきに関する検定1:カイ二乗検定」をご参考ください。

\[\]
④問題を解いてみる
ばらつきに関する検定のイメージができたと思うので、問題を解いて確認しましょう。
問)ある母集団から11個のサンプルを抽出したとき、不偏分散は3.56だった。信頼度95%で母分散の信頼区間を求めよ。
自由度は\(11-1\) で10、信頼度は95%なので、\(\frac{α}{2}=0.025,\frac{1-α}{2}=0.975\) よって、
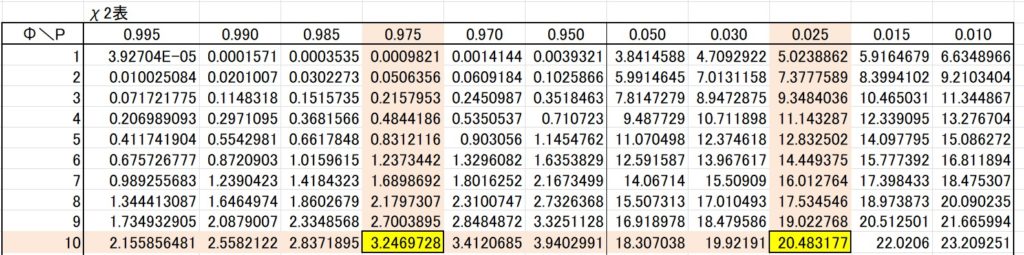
\[χ^2(10,0.975)=3.24697\]
\[χ^2(10,0.025)=20.4832\]
あとは平方和\(S\)が分かればよいのですが・・・問題文中に平方和がありません
;(´◦ω◦`):
\[\]
しかし、不偏分散は与えられています。
\[不偏分散=\frac{平方和}{自由度}\]
なので、 平方和=不偏分散×自由度 =35.6 となります。
よって、母分散の信頼区間の上限と下限は、それぞれ
\[σ^2=\frac{S}{χ^2(Φ,\frac{1-α}{2})}=\frac{35.6}{3.24697} =10.96\]
\[σ^2=\frac{S}{χ^2(Φ,\frac{1-α}{2})}=\frac{35.6}{20.4832} =1.738\]
よって、母分散の信頼区間は、1.738~10.96 となります。
\[\]
ここでpoint!
問題文によっては母標準偏差の信頼区間を聞いていくる場合があります。
しかし心配しないでください、\(母標準偏差=\sqrt{母分散}\)なので、信頼区間を計算方法は同じです。
最後に平方根の計算をチャチャっとしてください。
\[\]
まとめ
①ばらつきの推定には不偏分散を使う
②ばらつきの区間推定には検定統計量\(χ^2\)カイ二乗を使う
③母分散の信頼区間は \(\frac{S}{χ^2(Φ,\frac{α}{2})} ≦ σ^2 ≦ \frac{S}{χ^2(Φ,\frac{1-α}{2})}\)
④問題では、平方和、自由度、母分散or母標準偏差 に気を付ける
\[\]
今回は少し短めの内容でしたが、次回は二項分布の検定・推定について学んでいきます。
二項分布やポアソン分布の検定・推定を学ぶと、いよいよ実践的になってきます。














