二項分布の考え方

公開日2020年3月14日 最終更新日 2022年5月7日
みなさんこんにちは、michiです。
前回の勉強で工程能力指数とは何かと、使いかたについて勉強しました。
今回は確率分布の一つ、二項分布について学んでいきます。
キーワード 「二項分布」「期待値」「分散」
\[\]
目次
①二項分布とは
Wikipedia によると、「結果が成功か失敗のいずれかである試行を独立にn回行ったときの成功回数を確率変数とする離散確率分布である。」 とあります。
簡単に言うと、「〇か×の二択の確率分布」です。
この説明はコインの表裏でよく例えられます。
例えば、コインを一回投げて表か裏のでる確率を考えると、下のグラフになります。
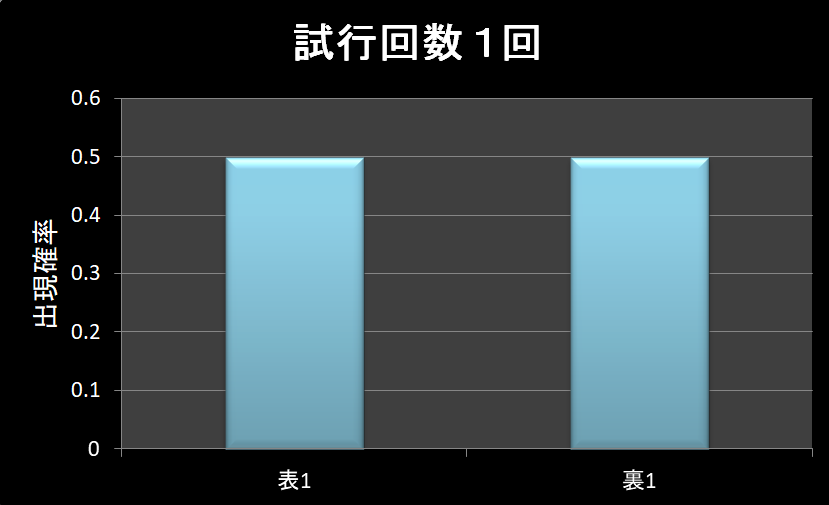
試行回数を2回にすると下のグラフになりますね。
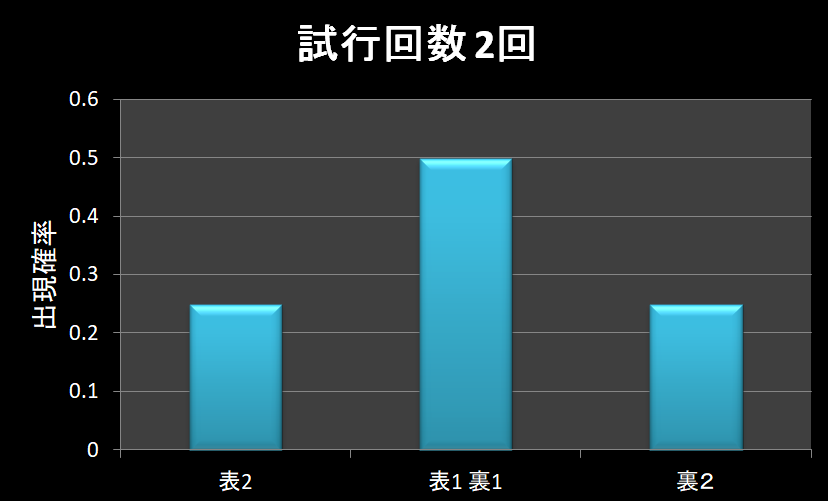
経験的にもわかると思いますが、試行回数を増やすとコインの表裏が同じくらい出る確率が上がります。
これをN回繰り返していくと、正規分布っぽい形になります。
※横軸を回数(N)縦軸をコインの表の数 としても同じになります。
\[\]
いきなり二項分布の説明をしましたが、なぜ品質管理に二項分布が必要なのでしょうか?
(。´・ω・)?
それは、製品の品質をコインの表裏で判断するから・・・・・・ではありません。
製品の品質は本来「正常か、異常か」の二択です。
例えば、車のワイパーが動かないけど、それ以外の品質は正常の場合を考えてみます。
もしみなさんが車の製造責任者であれば、この車は壊れている(異常である)と判断するでしょう。
ひとつでも「異常」があれば、品質的には「異常」です。
※ワイパーが使えなくても、「めったに雨の降らない地域だから大丈夫」という判断は、使用者の気持ちであって、製品の品質ではないです。
\[\]
前置きが長くなりましたが、この二択という状況はコインの表裏に似ています。
ただし、製品が正常か異常かは1/2の確率ではないはずです。
( ゚ω゚))コクコク
二項分布を使うことで、確率pで壊れるものをN回使用したときの分布(故障数)を推測することができます。
\[\]
②二項分布の式
二項分布は以下の式で表される確率分布です。
\[ P(x) = \scriptsize{n}\large{C}\scriptsize{x} × p^ x × (1-p)^{n-x} \]
先頭の \(\scriptsize{n}\large{C}\scriptsize{x}\) は見たことはあるけど・・・というかたも多いのではないでしょうか。
高校の数学の組合せで出てきたので少し復習をしましょう。
\[\scriptsize{n}\large{C}\scriptsize{x} = \frac{n!}{(n-x)! × x!}\]
・・・(。´・ω・)?
💦実数を入れてみるとわかりやすくなります。n=7, x=3 の場合は、
\[\scriptsize{7}\large{C}\scriptsize{3} = \frac{7!}{(7-3)! × 3!}=\frac{7・6・5・4・3・2・1}{(4・3・2・1) (3・2・1)}\]
\[=\frac{7・6・5}{3・2・1} \]
\[ =35\]
分子は、\(x\)の数だけ\(n\)の数字を下げていき掛け算します。
上の例題では\(7×6×5\) となります。
分母は、\(x\)の階乗になります。
上の例題では\(3×2×1\) となります。
\[\]
場合の数 \(\scriptsize{n}\large{C}\scriptsize{x} \)を掛ける理由は、確率\(p\)のイベントが\(n\)回中どの\(x\)回で起こるかの組合せを考慮しています。
この項が二項分布が正規分布っぽくなる要因です。

\[\]
\(p\)は0~1の間の「何かが生じる確率」で、\(1-p\)は逆に「何かが生じない確率」を表します。
\(p^ x × (1-p)^{n-x}\)は、
「何かが生じる確率」の\(x\)乗 × 「何かが生じない確率」の\((n-x)\)乗 を意味します。
\[\]
二項分布は一般的に \(Bi(n,p)\) とか\(B(n,p)\) と表現します。※\(n\)は試行回数、\(p\)はその確率。
\(Bi/B\)の由来は、二項分布の英語「Binominal distribution」からきています。
\[ P(x) = \scriptsize{n}\large{C}\scriptsize{x} × p^ x × (1-p)^{n-x} \]
\[\]
③二項分布の期待値と分散
二項分布の期待値\(E(X)\) と分散\(V(X)\) は以下の式で表されます。
\[E(X)=np,\qquad V(X)={np(1-p)}\]
「期待値\(E(X)\) = 試行回数\(n\) × 何かが生じる確率\(p\)」 です。
ところで、みなさんは「平均値」と「期待値」の違いをご存知でしょうか。二項分布などの確率分布では、「期待値」が使われます。
- 平均値:測定値の合計を測定数で割った値(算術平均)
- 期待値:各測定値にその確率を掛けた合計
コインを6回投げた場合を考えてみましょう。表の数×1 点とすると、「1,2,1,5,4,3,」と出た場合の平均値は 2.66 ですが、期待値は、
\[ 0× \frac{1}{64} + 1× \frac{6}{64}+ ・・・ + 6× \frac{1}{64}\]
\(=3\) となります。
この場合「期待値\(E(X)\) = (得点 × その得点が出る確率) の合計」 です。
\(E(X)=np= 6(回)×\frac{1}{2}(確率)=3\) と同じ結果になることを確認してください。
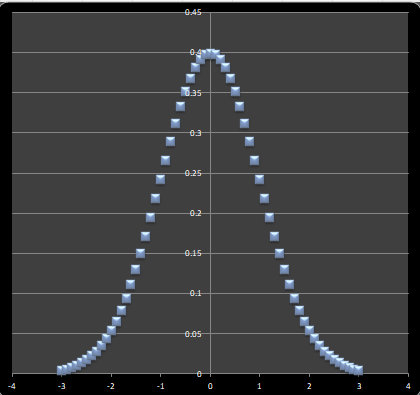
下のグラフがコインを6回投げた時の確率分布です。
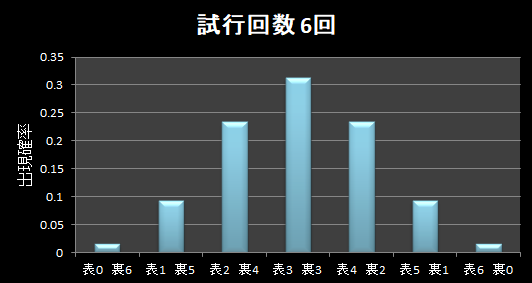
たしかに正規分布っぽくなってきました。
\[\]
最後に「分散」です。
「分散」は「期待値」を中心にどの程度ばらつくのか定量的に表した値です。
「分散\(V(X)\) = 期待値(\(np\)) × 確率\(p\)が生じない確率(\(1-p\))」 で表されます。
\[\]
試行回数\(n\)が増えれば分散(とりうる値の範囲)は増えます。
試行回数\(n\)が同じ場合は、確率\(p=\frac{1}{2}\)の時に分散が最大になります。
コインの表裏の重さに偏りのあるイカサマコインの場合、表裏の結果は偏ります(=ばらつきが小さくなる)。
\[\]
測定結果が、「期待値」や「分散」から考えてありうる値なのか、ありえない値なのかを評価していくことを「検定」と言います。
また、「期待値」からどのくらいの範囲がとりうる値なのか、とりうる値は何かを予測することを「推定」と言います。
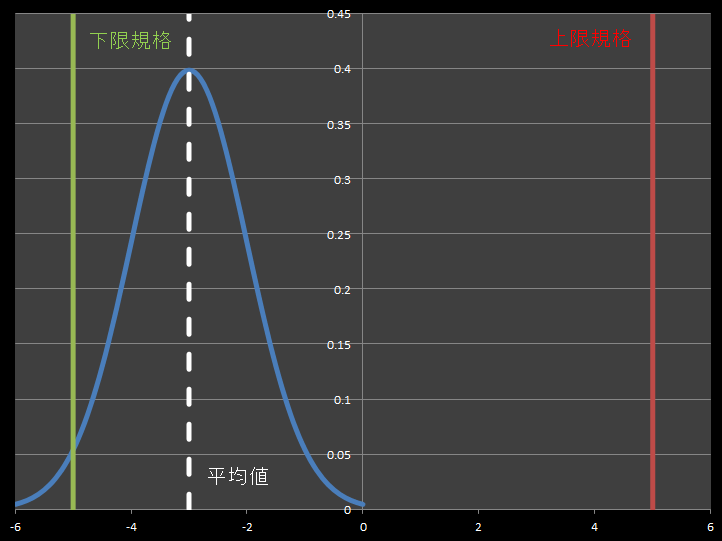
「期待値」が同じであっても「分散」が大きいと、推定値は大きな幅をもってしまいます。
「検定」と「推定」にはいくつか種類があるので、またの機会に勉強していきましょう。
\[\]
まとめ
①二項分布は〇×で判定されるものの確認分布
②二項分布の確率分布式は、\(P(x) = \scriptsize{n}\large{C}\scriptsize{x} × p^ x × (1-p)^{n-x}\)
③二項分布の「期待値\(E(X)=np\)」「分散\(V(X)={np(1-p)}\)」
次回は、期待値の式の導出を学んでいきましょう!(ちょっと厄介)













[…] でした。詳細は記事「二項分布の考え方」「二項分布期待値の導出」をご参考ください。 […]
[…] 詳細は記事「二項分布の考え方」をご参照ください。 […]
[…] 次回は二項分布の考え方について説明していきます。 […]
[…] 今回は前回の記事「二項分布の考え方」で出てきた二項分布の期待値の導出を行います。 […]
[…] 前回までは二項分布について考えてきましたが、QC検定2級では「ポアソン分布」という確率分布も出題されます。 […]
[…] 前回までに二項分布とポアソン分布という二種類の確率分布を学びました。 […]