相関関係２　大波・小波の相関

公開日2020年7月11日 　最終更新日 2023年3月4日

みなさんこんにちは、michiです。

前回の記事では、相関係数について初歩的なことを学びました。

今回は相関関係2と称して、前回の記事では学びきれなかったことを勉強します。

キーワード：「寄与率」「大波の相関」「小波の相関」

①寄与率

寄与率\(r^2\) は以下の式で表されます。

\[r^2=(\frac{S_{xy}}{\sqrt{S_x}×\sqrt{S_y}})^2=\frac{S_{xy}^2}{S_x×S_y}\]

(´･ω･)?(･ω･｀)

前回は二つの相関関係を判断するために、相関係数\(r\) を学びました。

\[r=\frac{S_{xy}}{\sqrt{S_x}×\sqrt{S_y}}\]

\(S_{xy}\): \(x\)と\(y\)の偏差積和、\(S_x\): \(x\)の平方和、\(S_y\): \(y\)の平方和

相関係数\(r\)の取りうる値は　\(-1 ≦ r ≦ 1\) の範囲内でした。

±1に近づくほど相関が強く、0に近づくほど相関が弱いと判断できるものでした。

このように、相関係数\(r\) で対象となるものどうしの関係を評価することができました。

ではなぜわざわざ相関係数\(r\) を二乗した寄与率\(r^2\) を考える必要があるのでしょうか？

(。´･ω･)?

その理由は次回の回帰分析の記事で説明しようと思います。

とりあえず、　「\((相関係数 r)^2\) = 寄与率\(r^2\) 」と覚えておきましょう。

\[\]

②大波の相関

相関関係をグラフから評価する方法に「大波の相関」と「小波の相関」があります。

大波の相関は以下の方法で求めます

• 中央値（メディアン）の線を引く
• 要因\(x\) と特性\(y\) は、中央値（メディアン）より大きければ「+」、小さければ「-」の符号とする
• 要因\(x\) と特性\(y\) の符号を掛け算し、各測定の 「+/-」 を決める
• すべての測定に対し行い、+ と – の数を数える
• + と – の数で少ないほうの数（\(n_+,n_-\)）を符号検定表の判定数\(n_s\) と比べる
• \(n_+≦n_s\)で負の相関、\(n_-≦n_s\)で正の相関　となる

\[\]

相関係数\(r\) を求めた時は、偏差積和や各平方和を求める必要がありました。

平方和の計算って、まぁちょっと面倒ですよね。

平方和の計算をしても、「正の相関がある」「負の相関がある」「相関がない」の３択ならもう少しシンプルに求めたいものです。

そこで、「大波の相関」や「小波の相関」を使います。

大波の相関では上に書いたように、「中央値」を求めたあとは中央値に対する大きさで「＋/ー」を決め、符号の掛け算した結果を数えるだけです。

(○´･ω･｀)bOK!

\[\]

それでは、大波の相関の解説をしていきます。

といっても、聞きなれない言葉があるので、そこから確認します。

要因\(x\) と特性\(y\) ですが、グラフを書く時のルールとして、横軸に要因（原因）を、縦軸に特性（結果）を書きます。

中央値に対して、要因（原因）が「＋/-」の時に、特性（結果）が「+/-」の数を数えています。

ここで疑問です。

なぜ「中央値」を使うのでしょうか？平均値ではだめなのでしょうか？

(。´･ω･)?

\[\]

相関係数\(r\)を求めるときには平方和を求めるために、平均値を使いました。

しかし大波の相関では中央値を使います。

その理由は、大波の相関では要因\(x\) と特性\(y\) の関係の数（符号が同じか否か）を、数えて判断しているためです。

イメージとしては、前回の相関係数の勉強で使用した下図の「青色の領域と赤色の領域に属する点の数を数えている」ことをしています。

\[\]

重要なことは、平均からのずれ具合を加味する平方和と違い、対応する符号の数を数えることです。

そのため、中央値を基準にして中央値より前のデータの要因\(x\) と特性\(y\) の関係、中央値より後のデータの要因\(x\) と特性\(y\) の関係を評価しています。

\[\]

③なぜ判定数は少ないほうの数で考えるのか

大波の相関では、要因\(x\) と特性\(y\) の符号関係に注目していることはわかりました。

しかし、なぜ「少ないほうの数」と「符号検定表の判定数」を比べるのでしょうか？

それを解説する前に、簡単に符号検定表（下表）について説明します。

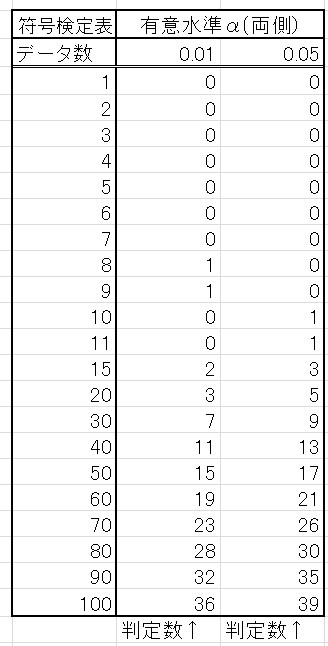
符号検定表には、データ数と有意水準α(1% or 5%）と有意水準αの下に判定数\(n_s\) が書かれています。

データ数が増えるほど判定個数\(n_s\) が増えていることが分かります。

この符号検定表では「逆の相関関係を示す符号の許容個数」が書かれています。

(。(*・ω・*)ﾝ？(*「･ω･)ﾝ？ヽ(*･ω･*)ﾉ･･･ﾊﾃ ???

\[\]

例えば、正の相関関係がある場合は、要因\(x\) が増えれば特性\(y\) も増えるので、グラフは右肩上がりの形になります。

グラフが右肩上がりということは、要因\(x\)<中央値 のときは特性\(y\)＜中央値で、要因\(x\)＞中央値のときは特性\(y\)＞中央値　になるはずです。

「はず」というのは、たまに例外があってもある有意水準αでは、許容されることを意味します。

\[\]

つまり大波の相関では、要因\(x\) と特性\(y\) の符号を掛け算したときに「ー」となる数\(n_-\)が符号検定表の判定数\(n_s\)以下であれば正の相関であると判定します。

逆に、要因\(x\) と特性\(y\) の符号を掛け算したときに「+」となる数\(n_+\)が符号検定表の判定数\(n_s\)以下であれば負の相関であると判定します。

\[\]

④小波の相関

小波の相関は、以下の方法で求めます

• 要因\(x\) と特性\(y\) は、それぞれ前のデータより大きければ「+」、小さければ「-」の符号とする
• 要因\(x\) と特性\(y\) の符号を掛け算し、各変化の 「+/-」 を決めるの + か – を決める
• すべての変化に対し行い、+ と – を数える
• + と – の数で少ないほうの数（\(n_+,n_-\)）を符号検定表の判定数\(n_s\) と比べる
• \(n_+≦n_s\)で負の相関、\(n_-≦n_s\)で正の相関　となる

各変化の符号「+/-」を決定してからは、大波の相関と同様の方法で相関関係を判定します。

\[\]

大波の相関と小波の相関の符号を決めるときの相違点は以下の通りです。

• 大波の相関：中央値に対する大小関係で「＋/-」の符号を決める。
• 小波の相関：前のデータに対する大小関係で「＋/-」の符号を決める。

なお、符号が「0」の場合は数えません。

大波の相関では中央値と同じ値のとき、小波の相関では前のデータから変化がない場合に該当します。

\[\]

⑤例題を解いてみる

大波の相関（中央値に対する大小）と小波の相関（前のデータに対する大小）を学んだので、例題を解いてみましょう。

下の表はあるダイエット日記を書いている人の20年7月以降の体重、脂肪率、筋肉量の推移です。

このデータを基に、体重と筋肉量の相関関係を求めてみます。

\[\]

　１：大波の相関でもとめてみる

体重と筋肉量についてデータをまとめ、中央値を求めると下表のようになりました。

下図にこの時のイメージを描きました。

中央値に対して上側を「＋」、下側を「ー」としています。

\[\]

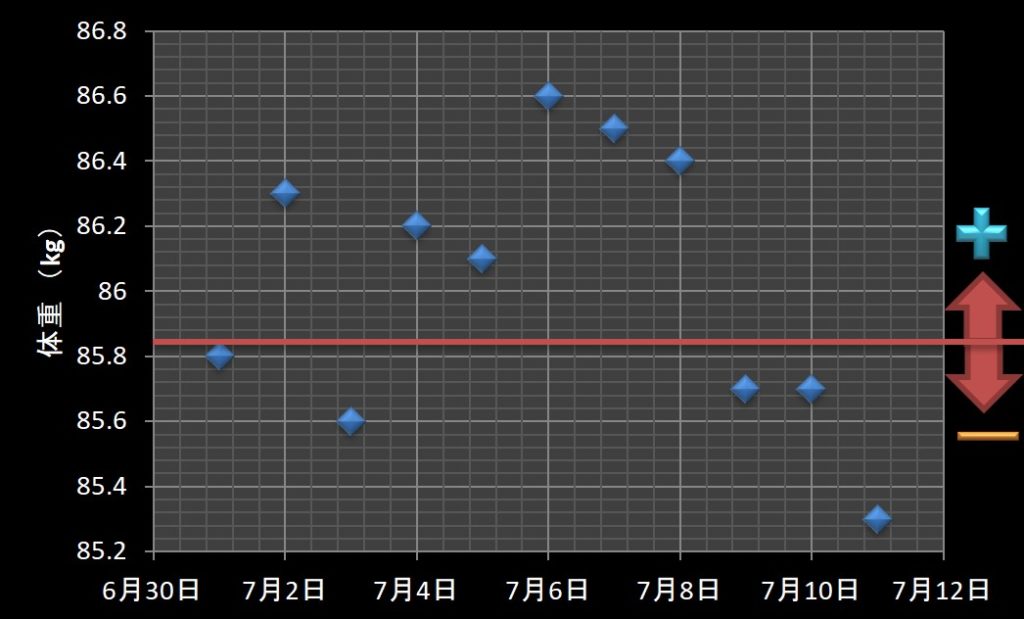
この時、体重の「+/-」と筋肉量の「+/-」を掛け算した結果の、＋の数とーの数を数えると、－の数の方が少ないです。

ですので、－の数\(n_-(=2)\)が、サンプル数11個の時の判定数\(n_s\)より小さければ相関があると判定できます。

すると、有意水準が5%の時で　－の数\(n_-=2\) ＞ 判定数\(n_s=1\)　となります。

－の数が判定数より大きいため、「正の相関はない」となります。

\[\]

　　２：小波の相関でもとめてみる

大波の相関では相関関係はないと判定しましたが、小波の相関でも求めてみましょう。

体重と筋肉量についてデータをまとめ、前のデータに対する増減は下表のようになりました。

下図にこの時のイメージを描きました。

前のデータにに対して増加していれば「＋」、減少していれば「ー」としています。

\[\]

大波の相関同様、体重の「+/-」と筋肉量の「+/-」を掛け算した結果の、＋の数とーの数を数えると、－の数の方が少ないです。

ですので、－の数\(n_-(=3)\)が、サンプル数10個の時の判定数\(n_s\)より小さければ相関があると判定できます。

すると、有意水準が5%の時で　－の数\(n_s=3\) ＞判定数\(n_s=1\)　となります。

－の数が判定数より大きいため、「正の相関はない」となります。

小波の相関では、大波の相関よりもサンプル数が一つ少なくなります。

理由は、小波の相関では変化分をみているからです。

\[\]

今回の判定では、体重の増加に対し、筋肉量の増加に相関関係はないとなりました。

しかし、今回のデータはデータ範囲が狭すぎるかもしれません。

一週間、一か月単位で見れば、相関関係は見えてくるかもしれませんね。

もしくは「変動の範囲内」なので、相関関係が見えないだけかも

話がそれましたね、最後に今回学んだことをまとめてみましょう。

\[\]

まとめ

①\((相関係数 r)^2\) = 寄与率\(r^2\)

②大波の相関は中央値に対する大小

③少ないほうの符号の数が、許容の範囲内か否かで相関関係を判定

④小波の相関は前のデータに対する大小　

⑤筋肉量と体重に正の相関はなさそう

\[\]

今回で相関分析に関する内容は一通り学びました。

次回からは、回帰分析について学んでいきましょう！

⇒オススメ書籍はこちら

⇒サイトマップ