回帰分析の手順

公開日2020年7月25日 　最終更新日 2021年9月20日

みなさんこんにちは、michiです。

前回の記事では回帰分析とは何かについて学びました。

今回は「回帰分析の手順」と称して、前回勉強しきれなかった実践編の勉強をしていきます。

キーワード：「分散分析表」「F検定」「寄与率」

①回帰分析の手順（前半）

回帰分析は以下の手順で進めます。

1. 得られたデータから、各平方和（ばらつき）を求める
2. 各平方和に対して、自由度を求める
3. 不偏分散と分散比を求める
4. 分散分析表を作る
5. F検定を行う
6. 回帰係数の推定を行う

\[\]

1.得られたデータから、各平方和（ばらつき）を求める

始めに総変動（\(S_T\))、回帰による変動(\(S_R\))、残差による変動(\(S_E\)) を求めます。

• \(S_T = S_y\)
• \(S_R = \frac{(S_{xy})^2}{S_x}\)
• \(S_E=S_T-S_R =S_y-\frac{(S_{xy})^2}{S_x}\)

計算式の導入は前回の記事「回帰分析とは」をご参照ください。

\[\]

2.各平方和に対して自由度を求める

全体の自由度(\(Φ_T\))、回帰の自由度(\(Φ_R\))、残差の自由度(\(Φ_E\)) を求めます。

自由度とは何かについては、記事「平方和ではだめ？不偏分散とは」をご参照ください。

回帰分析に必要な自由度は下記の通りです。

• 全体の自由度　　：データ数ー１
• 回帰による自由度：１
• 残差による自由度：全体の自由度－回帰による自由度＝データ数ー２

回帰の自由度は、常に「１」になります。

なぜなら、単回帰分析では、回帰直線をただ一つ定めて仮説を検定するからです。

残差の自由度は、全体の自由度から回帰の自由度を引いたものになります。

\[\]

3.不偏分散と分散比を求める

平方和と自由度がわかったので、不偏分散を求めることができます。

不偏分散は以下の式で求めることができました。

\[不偏分散(V)=\frac{平方和(S)}{自由度(Φ)}\]

（関連記事「平方和ではだめ？不偏分散とは」）

今求めようとしている不偏分散は、回帰による不偏分散と残差による不偏分散ですので、

\[V_R=\frac{S_R}{Φ_R}=S_R \qquad V_E=\frac{S_E}{Φ_E}=\frac{S_E}{n-2}\]

F検定を行うための検定統計量\(F_0\) は、

\[F_0=\frac{V_R}{V_E}\]

となります。

記事「ばらつきに関する検定2:F検定」では、\(F_0>1\) となるように、分母と分子を入れ替える（設定する）と記載しました。

しかし、回帰分析においては、\(F_0=\frac{V_R}{V_E}\)　となります。

分子は回帰による不偏分散、分母は残差による不偏分散で決まっています。

なぜなのかは後ほど・・・

(。´･ω･)?

\[\]

4.分散分析表を作る

1～3で行った計算をした表のようにまとめます。

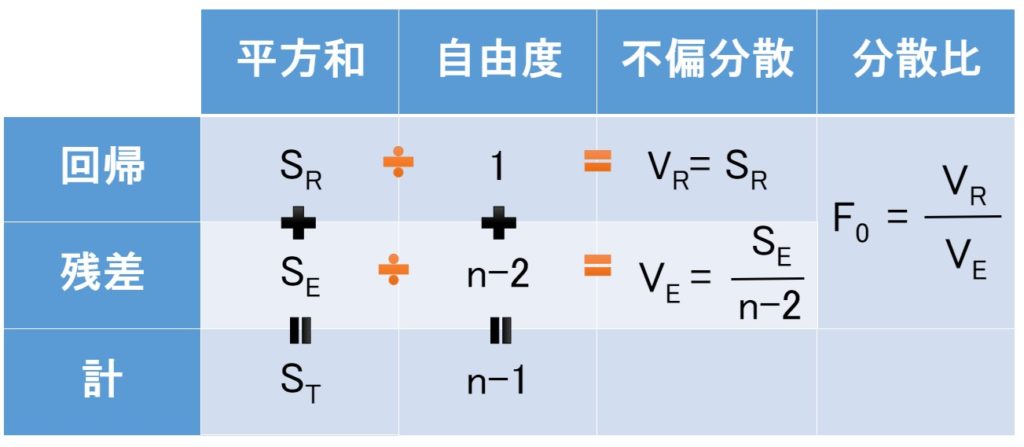
この表を分散分析表というのですが、QC検定では頻出します。

\[\]

②回帰分析の手順（後半）

5.F検定を行う

「3.不偏分散と分散比を求める」で求めた検定統計量\(F_0\)に対して、F検定を行います。

関連記事（ばらつきに関する検定2:F検定）

検定をするということは、何かしらの仮説に対してその有意性を確認しています。

回帰分析における仮説とは「回帰による変動は、残差による変動よりも、全体に与える影響が大きい」です。

簡単に言うと、「回帰直線引いたけど、意味あんの？」を検定します。

イメージとしては、下の二つの図を比べてみたください。

どっちも回帰直線を引いています。

例1は直線を引いた意味がありそうですが、例2は直線を引いた意味がなさそうですよね・・・

というより、例２はどうやって直線引いたの？って感じです。

(ﾟωﾟ*)(｡ω｡*)(ﾟωﾟ*)(｡ω｡*)ｳﾝｳﾝ

\[\]

では実際にF検定をしてみましょう。

\[分散比 F_0= \frac{V_R}{V_E}\qquad >\qquad F表のF(1,n-2:α)\]

が成立すれば、「回帰直線は意味のあることだ」と判定します。

※この時の帰無仮説は「\(β=0\): \(x\)と\(y\)に関係はない」ですが、分散比\(F_0\)がF表の値より大きい場合、この帰無仮説が棄却されます。

\[\]

\(F(1,n-2:α)\) は、\(F\)(分子の自由度、分母の自由度：有意水準) を表します。

分子の自由度は回帰による自由度なので「１」、分母の自由度は「データ数ー２」、有意水準は基本的に5%が多いです。

\[\]

F表では、横軸（行）に分子の自由度が、縦軸（列）に分母の自由度が並んでいて、その交わるところの数値が、F表の値になります。

例えば、データ数12、有意水準5%の回帰分析を行った場合、4.96となります。

※\(F\)(1,12-2:0.05)の値になります。

\[\]

6.回帰係数の推定を行う

「5.F検定を行う」で「回帰による変動は、残差による変動よりも、全体に与える影響が大きい」と判定された場合、回帰係数の推定を行います。

推定値\(α,β\) は、前回の記事「回帰分析とは」より、

\[α=\bar{y}-β\bar{x},\qquad β=\frac{S_{xy}}{S_x}\]

計算した推定値を回帰式 \(y=α+βx\) に代入して求めます。

\[\]

以上が、回帰分析の手順になります。

回帰分析では「回帰による変動\(S_R\) と、回帰式の推定値\(β\)」が間違いやすいので、気をつけましょう！

\[S_R = \frac{(S_{xy})^2}{S_x} \qquad β=\frac{S_{xy}}{S_x}\]　

ですよ！

(◎｀・ω・´)ゞﾗｼﾞｬ

\[\]

③実例を解いてみる

理論だけ勉強してもしょうがないので、問題を解いてみましょう

問）標本数12組のデータで、\(x\)の平均が4、平方和が15、\(y\)の平均が8、平方和が10、\(x\)と\(y\)の偏差積和が9の時、回帰による検定を有意水準5%で行い、判定が有意となったときは、回帰式を求めてね

\[\]

それでは早速問題を解いてみましょう。

1.得られたデータから、各平方和（ばらつき）を求める

\[S_T=S_y\qquad S_R=\frac{(S_{xy})^2}{S_x}\qquad S_E=S_T-S_R\]

より、問題文から該当する値を代入すると、

\[S_T=10\qquad S_R=\frac{9×9}{15}=5.4\qquad S_E=10-5.4=4.6\]

\[\]

2.各平方和に対して自由度を求める

回帰による自由度\(Φ_R=1\)、残差による自由度\(Φ_E=12-2=10\)

\[\]

3.不偏分散と分散比を求める

1,2 より、平方和と自由度がわかったので、

\[V_R=\frac{S_R}{Φ_R}=\frac{5.4}{1}=5.4 \qquad V_E=\frac{S_E}{Φ_E}=\frac{4.6}{10}=0.46\]

よって分散比\(F_0\) は、

\[F_0=\frac{5.4}{0.4}=11.739\]

\[\]

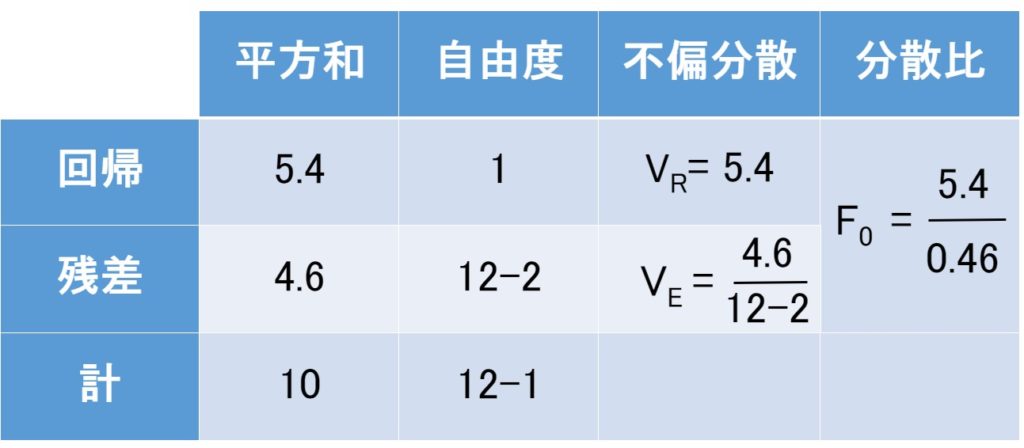
4.分散分析表を作る

1～3をまとめると、下表のようになります。

\[\]

5.F検定を行う

得られた分散比\(F_0\) に対してF検定を行うと、

\[分散比 F_0=11.739 \qquad > \qquad F(1,10:0.05)=4.96\]

よって、回帰直線による変動は有意であると判定されます。

\[\]

※回帰による変動は、残差による変動より全体に与える影響が大きい

\(F(1,10:0.05\) の値は下表を参考にしてください。

\[\]

6.回帰係数による推定を行う

「5.F検定を行う」より回帰直線を考えることは有意であるのと判定できました。

ですので、問題文にしたがって回帰直線を考えます。

回帰式を　\(y=α+βx\) とすると、

\[α=\bar{y}-β\bar{x} \qquad β=\frac{S_{xy}}{S_x} \]

より、

\[β=\frac{S_{xy}}{S_x}=\frac{9}{15}=0.6\]

\[α=\bar{y}-β\bar{x}=10-0.6×4=7.6\]

よって、回帰式は、

\[y=7.6+0.6x\]

(｀･ω･´)ﾄﾞﾔｯ!

\[\]

④寄与率を求める

実例を解いてみましたが、QC検定では寄与率を求めてくる場合も多いです。

寄与率は以下の式で計算されます。

\[寄与率(R)=\frac{回帰による変動(S_R)}{全体の変動(S_T)}\]

回帰による変動(\(S-R\)) ≦ 全体の変動(\(S_T\)) が常に成り立つので、寄与率は0～1の間の数値となります。

・・・どこかで聞いたような・・・.ﾟ+.(´∀｀*).+ﾟ.

\[\]

さて寄与率\(R\) を平方和の形に書き直してみます。すると、

\[R=\frac{S_R}{S_T}=\frac{(S_{xy})^2}{S_x}÷S_y=\frac{(S_{xy})^2}{S_x・S_y}=(\frac{S_{xy}}{\sqrt{S_x}・\sqrt{S_y}})^2\]

なんと、寄与率は相関係数\(r\) の二乗と同じになりました！

※詳しくは、記事（相関関係2 大波・小波の相関）をご参照ください。

\[\]

滅多にないとは思いますが、偏差積和が問題文中に書かれていなくて、相関係数や寄与率から、回帰分析を行う問題も作れそうです・・・

(´⊃･∀･｀)⊃ﾏｱﾏｱ…

\[\]

まとめ

①②回帰分析は以下の手順で行う

1. 得られたデータから、各平方和（ばらつき）を求める
2. 各平方和に対して、自由度を求める
3. 不偏分散と分散比を求める
4. 分散分析表を作る
5. F検定を行う
6. 回帰係数の推定を行う

③問題は、とにかく解くべし

④(相関係数)\(^2\)=寄与率

\[\]

今回で回帰分析の話は終了です。

次回からは実験計画法について勉強していきます。

また次回もよろしくお願いします。

⇒オススメ書籍はこちら

⇒サイトマップ