F分布とは

公開日2020年4月29日 最終更新日 2022年6月19日
みなさんこんにちは、michiです。
前回勉強した「\(χ^2\)カイ二乗分布とは」では、母分散と標本の分散のばらつきを評価していました。
今回も「ばらつき」を評価するための分布 F分布について学んでいきます。
キーワード:「F分布」
目次
①F分布とは何か
F分布とは、「二つの標本のばらつきを評価する検定統計量」です。
F分布の定義式は以下のとおりです。
\[F=\quad \frac{σ_2^2}{σ_1^2}・\frac{V_1}{V_2}\]
\(σ_1,σ_2\)は母標準偏差1,2 を、\(V_1,V_2\)は不偏分散1,2をそれぞれ表します。
この式だけ見ても、「(* ̄ω ̄)ふーんそうなんだ…で?」で終わりそうです。
\[\]
式の意味について考えていきますが、その前に前回の記事の\(χ^2\)カイ二乗分布について復習をしましょう。
\[\]
\[χ^2=Φ\frac{s^2}{σ^2}=自由度 × \frac{標本の標準偏差^2(=不偏分散)}{母標準偏差^2(=母分散)}\]

\(χ^2\)カイ二乗分布では、一つの母集団から抽出されたサンプルの分散を評価していました。
それがF分布では、母標準偏差1,2( \(σ_1,σ_2\))と、不偏分散1,2(\(V_1,V_2\))のそれぞれ二種類のパラメータがあります。
つまりF分布では「二つの母集団から抽出された二つの標本を評価」します。
\[\]
②F分布の式の導出
F分布は\(F=\frac{σ_2^2}{σ_1^2}・\frac{V_1}{V_2}\) であるといいましたが、その意味は何でしょうか?
(。´・ω・)?
\[\]
F分布は二つの集団の分散を評価するので、前回学んだ\(χ^2\)カイ二乗分布を二つ用意して、その比を評価(割り算)すれば導出できそうです。
計算しやすいように、\(χ^2\)の値を変形させます。
(詳細は「カイ二乗分布とは」をご参考ください)
\[χ^2=Z_1^2+Z_2^2+・・・+Z_n^2\]
\[=(\frac{x_1-μ}{σ})^2+(\frac{x_2-μ}{σ})^2+・・・(\frac{x_n-μ}{σ})^2\]
この式変形は、統計量\(Z\)を展開しただけです。
分母の\(σ\)をひとまとめにし、自由度\((n-1)\)を分母と分子にかけて
\[=(\frac{x_1-μ}{σ})^2+(\frac{x_2-μ}{σ})^2+・・・(\frac{x_n-μ}{σ})^2\]
\[=\frac{n-1}{σ^2}・\frac{1}{n-1}((x_1-μ)^2+(x_2-μ)^2+・・・(x_n-μ)^2)\]
\[=\frac{n-1}{σ^2}・\frac{S}{n-1}\]
\[※平方和 S = (x_1-μ)^2+(x_2-μ)^2+・・・(x_n-μ)^2\]
さて、右側の項に着目すると、これは不偏分散(=V)の形になりました。よって、
\[※不偏分散\quad V=\frac{S}{n-1}=\frac{平方和}{自由度}\]
\[χ^2=\frac{n-1}{σ^2}・\frac{1}{n-1}((x_1-μ)^2+(x_2-μ)^2+・・・(x_n-μ)^2)\]
\[=\frac{(n-1)V}{σ^2}\]
これで\(χ^2\)式がみやすくなりました。
次に、二つのカイ二乗分布\(χ_1,χ_2\)の比を求めると、
\[\frac{χ_1^2}{χ_2^2}=\frac{\frac{(n-1)V_1}{σ_1^2}}{\frac{(m-1)V_2}{σ_2^2}}\]
※標本1の母集団の自由度を\((n-1)\)、標本2の母集団の自由度を\((m-1)\)とした
・・・
この式は誤りです!
Σ(・ω・ノ)ノ!
この式の問題は「自由度」です。
\(χ^2\)カイ二乗分布は、自由度によってその分布の形が変わる特徴がありました。
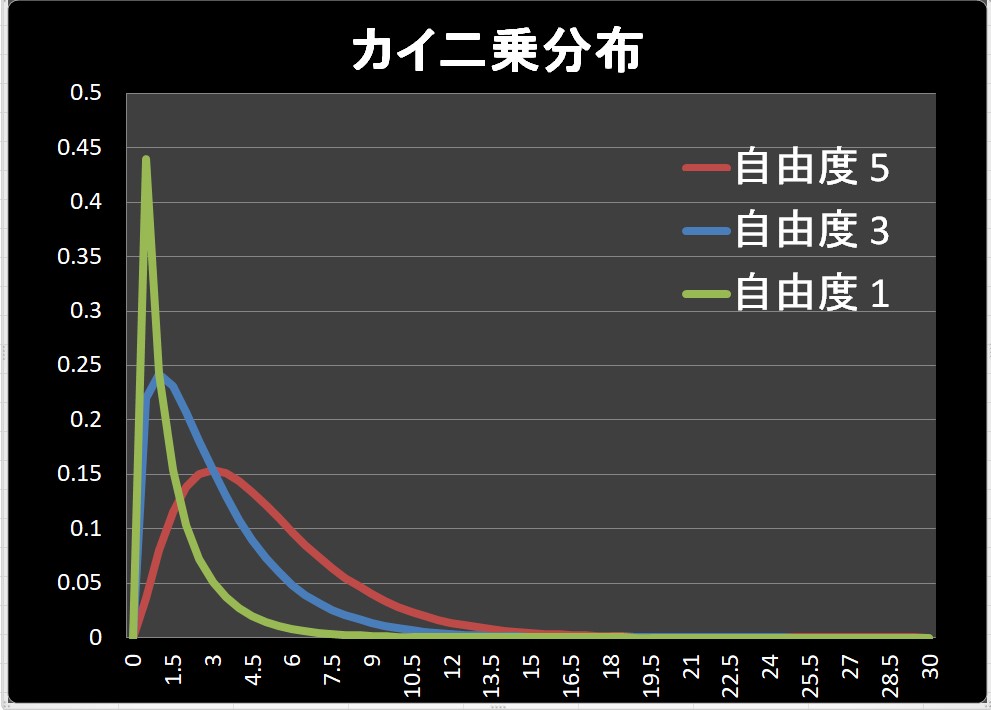
このまま二つの標本を比較しようとしても、自由度が異なるため単純な比計算ができません。
そこで、\(χ^2\)をそれぞれの自由度で割り算した値を比較します。
そうすることで、「自由度あたりの\(χ^2\)」を比較できるようになります。
よって、
\[F=\frac{\frac{(n-1)V_1}{σ_1^2}・\frac{1}{n-1}}{\frac{(m-1)V_2}{σ_2^2}・\frac{1}{m-1}}\]
\[=\frac{\frac{V_1}{σ_1^2}}{\frac{V_2}{σ_2^2}}\]
\[=\frac{V_1}{σ_1^2}・\frac{σ_2^2}{V_2}\]
\[=\frac{σ_2^2}{σ_1^2}・\frac{V_1}{V_2}\]
これで、F分布の式が導き出せました。
ε-(´∀`*)ホッ
\[\]
③F分布の形
F分布の式を導出できたので、F分布グラフがどのような形になるのか確認してみましょう。

F分布が左右非対称な形なのは、\(χ^2\)カイ二乗分布を基にしているからです。
また、自由度によって形が変わるのも\(χ^2\)カイ二乗分布とおなじですよね。
このグラフをよく見ると、疑問が生じますよね?
「母標準偏差がない!」 Σ(・ω・ノ)
\[\]
F分布は、定義より二つの母標準偏差と二つの標本の標準偏差の比で求められました。
が、上のグラフでは母標準偏差を無視しています。
QC検定2級で出題される問題は、通常「一つの母標準偏差のみで問われる」場合が多いので、今回はその場合を想定しています。
\[\]
つまり、「一つの母集団から二つの標本の標準偏差」を比較することになるのですが、この際 \(σ_1=σ_2\) となるので、\(\frac{σ_2^2}{σ_1^2}=1\)となります。
つまり、\(F=\frac{σ_2^2}{σ_1^2}・\frac{V_1}{V_2}=\frac{V_1}{V_2}\) です。
\[\]
一つの母集団?そんな場合があるの?(。´・ω・)? って思いますよね。
例えば、製品Aを毎日製造する装置がある場合を考えます。
同じ装置で作られている製品Aは、同じ程度の「ばらつき」(=製品精度)のはずです。
つまり、同じ母標準偏差となるはずです。
この製品Aの「ばらつき」が安定しているかを評価するために、定期的にサンプルを抽出して評価する際にF分布が有効になります。

\[\]
④F分布の注意点
ここまで、F分布とは何かについて学んで来ましたが、注意点があります。
それは以下の三点です。
- 比較する分散が独立であること
- 検定統計量F \(>1\) となるように設定すること
- 二つの自由度があること
「比較する分散が独立であること」について、比較する分散が独立でない場合、共分散の項がでてきてしまいます。
共分散の項がでると、単純な不偏分散の比の計算ができなくなってしまいます。
φ(´・ω・`)メモメモ
\[\]
「検定統計量F \(>1\) 」は、検定・推定をする際に必要となる条件です。
F\(<1\)となった場合は、分子と分母を入れ替えて、F \(>1\)となるように設定しましょう。
\[\]
「二つの自由度があること」は、二つの標本を比較しているので当たり前といえば当たり前です。
見方をかえると、「抽出するサンプル数が異なっていても評価できる」ことを意味します。

\[\]
まとめ
①F分布では、二つの母集団から抽出された二つの標本を評価
②F分布は、二つの\(χ^2\)カイ二乗分布を自由度で割った値の比を評価
③QC検定では通常一つの母集団、二つの不偏分散の問題がだされる
④F分布の注意点は三つ「独立した分散、F \(>1\)、自由度が2つ」
\[\]
今回はF分布とは何かについて勉強しました。F分布を使った検定や推定の方法については、またの機会にまとめます。
次回はt分布について勉強していきましょう!














[…] 次回はF分布について勉強していきましょう! […]