平均値に関する推定

公開日2020年5月10日 　最終更新日 2022年1月22日

みなさんこんにちは、michiです。

前回までは検定について平均値と分散について学びました。

※前回はF検定における左側の棄却限界値の求め方を学びました。

今回は推定を行い、具体的な数値を求める方法について勉強します。

キーワード：「点推定」「区画推定」

\[\]

①推定とは

推定とは、得られた標本から母集団の性質を予測することです。

代表的なものに点推定と区間推定があります。

• 点推定とは、標本から得られたデータでただ一つの値を求めること
• 区間推定とは、母集団の真の値が任意の確率であてはまる範囲を求めること

点推定の方法には、モーメント法と最尤法（さいゆうほう）がありますが、QC検定2級ではモーメント法が分かれば十分です。

※尤とは「もっともらしい」という英語のlikelyの日本語訳です。

\[\]

②平均値の点推定

平均値の点推定の値は、得られた標本の合計値をサンプル数で割った値になります。

\[E(X)=\frac{X_1+X_2+・・・+X_n}{n}\]

標本から得られた点推定の平均値が、「必ずしも母集団の平均値を等しくなるとは限らない」ので、気を付けましょう。

モーメント法とは、得られた標本のデータから母集団を推定することです。

確率分布が「正規分布」「t分布」「二項分布」「ポアソン分布」の場合に、モーメント法が有効となります。

\[\]

③平均値の区間推定

点推定では、標本から得られたデータで、母集団の値をひとつに決めました。

しかし、標本のみでは母集団すべてを調べたわけではないので、真の値とずれがあります。

\[\]

例えば次の例を考えてみましょう。Aさん～Jさんの数学のテストの点です。

この10人全員を母集団としたときのテストの平均値は　53 点です。

しかし標本データとして、Aさん～Eさんの5人のデータを抽出した場合の平均値は　38点で、Fさん～Jさんの場合は　68点です。

いずれも母集団の平均値である　53点からずれています。

\[\]

このように、標本データのみでは母平均の真の値を特定することは難しいです。

しかし、標本データから「おおむね○○点～○○点のあいだに母平均があるだろう」と推測は可能です。

この範囲を推定することを、区間推定といいます。

またその範囲を信頼区間といいます。

※似た言葉に予測区間がありますが、QC検定2級では出ません

\[\]

区間推定では「おおむね・・・だろう」といいました。このように、推定の精度にはある程度の不確かさがあります。

推定の精度は95%に設定されることが多く、その設定を「信頼度95%」といいます。

\[\]

④区間推定の区間の設定方法

区間推定の詳細に入る前に、検定で学んだことをおさらいします。

検定では「統計量」を計算し、その「統計量」が「採択域内」か「棄却域内」かで仮説の妥当性を判断しました。

推定は、この「採択域」の範囲を求めることと解釈できます。

この時の注意点は以下の2点です。

1. 標本平均が採択域の中心にくるように設定
2. 棄却域は標本平均から同じだけ離れた値に設定

\[\]

この設定をする理由について、考えてみましょう。

「1.標本平均が採択域の中心にくるように設定」ですが、標本平均は母平均に近いと仮定しています。

標本平均は母平均から離れていると仮定をすると、そもそも推定自体ができません。

\[\]

「2.棄却域は標本平均から同じだけ離れた値に設定」ですが、もし棄却域を片側のみに設定した場合、棄却域を設定した人は標本平均と母平均の大小関係を把握していることになります。

母平均の値がわからないため、標本平均から母平均を見積もるのです。

片側のみに棄却域を設定することは、答え（母平均）を知らないとできません。

以上を踏まえ、区間推定を実践していきましょう。

\[\]

⑤正規分布の区間推定

信頼度を1-\(α\)%として、区間推定を考えてみます。

確率\(α\)が区間推定の外に真の値がある確率で表されます。

正規分布の統計量\(Z\)は以下の式です。

\[Z=\frac{\bar{x}-μ}{\frac{σ}{\sqrt{n}}}\]

\(\bar{x}\):標本平均、\(μ\):母平均、\(σ\):母標準偏差、\(n\):サンプル数

この統計量\(Z\)が採択域の　\(-Z(\frac{α}{2})\)、\(Z(\frac{α}{2})\)の範囲内にあるので

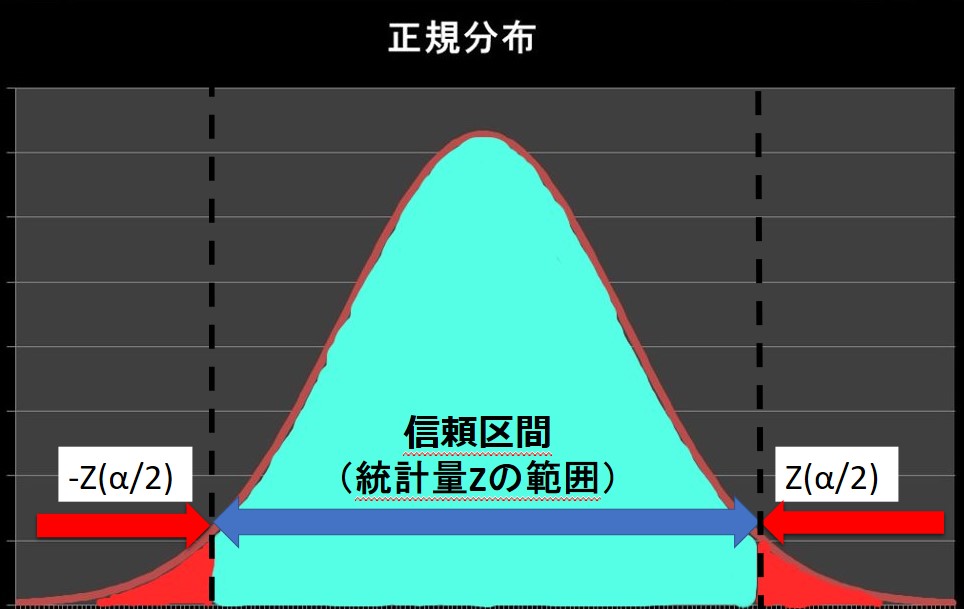
\[-Z(\frac{α}{2})≦\frac{\bar{x}-μ}{\frac{σ}{\sqrt{n}}}≦Z(\frac{α}{2})\]

母平均\(μ\)の範囲が分かるように式変形をして

\[-Z(\frac{α}{2})×\frac{σ}{\sqrt{n}}≦\bar{x}-μ≦Z(\frac{α}{2})×\frac{σ}{\sqrt{n}}\]

\[-\bar{x}-Z(\frac{α}{2})×\frac{σ}{\sqrt{n}}≦-μ≦-\bar{x}+Z(\frac{α}{2})×\frac{σ}{\sqrt{n}}\]

\[\bar{x}-Z(\frac{α}{2})×\frac{σ}{\sqrt{n}}≦μ≦\bar{x}+Z(\frac{α}{2})×\frac{σ}{\sqrt{n}}\]

\[\]

正規分布における平均値の区間推定を問われる場合は、母標準偏差\(σ\)や、標本平均\(\bar{x}\)、標本のサンプル数\(n\)と確率\(α\)がわかれば解けます。

では、実際に問題を解いてみましょう。

\[\]

問）母分散\(σ^2=3^2\)とわかっている母集団から、16個のサンプルを抽出した。その時の平均値は30だった。信頼度95%で母平均の信頼区間を求めよ。

信頼区間を求めるためのパラメータは、\(\bar{x}=30\)、\(n=16\)、\(σ=3\)です。正規分布表の「PからKpを求める表」より\(\frac{α}{2}\)=\(\frac{0.5}{2}\)=0.025　なので、

\[Z(\frac{α}{2})=1.960\]

よって、信頼区間の上限と下限は

\[\bar{x}+Z(\frac{α}{2})×\frac{σ}{\sqrt{n}}=30+1.960×\frac{3}{\sqrt{16}}=31.47\]

\[\bar{x}+Z(\frac{α}{2})×\frac{σ}{\sqrt{n}}=30-1.960×\frac{3}{\sqrt{16}}=28.53\]

よって信頼区間は、28.53～31.47

標本平均は30でしたが、95%の確率で母平均は　28.53～31.47　の区間内の数値であると計算できました。

\[\]

⑥\(t\)分布の区間推定

先ほどは母集団の母標準偏差がわかっていたので、正規分布表を使って信頼区間を求めることができました。

しかし、母標準偏差が分かるけど母平均がわからない状態というのは考えづらいです。

そこで標本データのみから信頼区間を求める\(t\)表を使った区間推定をしてみましょう。

\[\]

使用する統計量\(t\)は検定の時と同じ式で求められ、正規分布の統計量\(Z\)の母分散\(σ^2\)を不偏分散\(V\)に置き換えればよいので、以下のようになります。

\[t=\frac{\bar{x}-μ}{\sqrt{\frac{V}{n}}}\]

先ほどと同じように問題を解いてみましょう。

\[\]

問）不偏分散\(V=9\)の標本集団を16個用意した。その時の平均値は30だった。信頼度95%で母平均の信頼区間を求めよ。

信頼区間を求めるためのパラメータは、\(\bar{x}=30\)、\(n=16\)、\(V=9\)です。\(t\)表では確率\(α\)=0.05　は両側確率で表されるので　

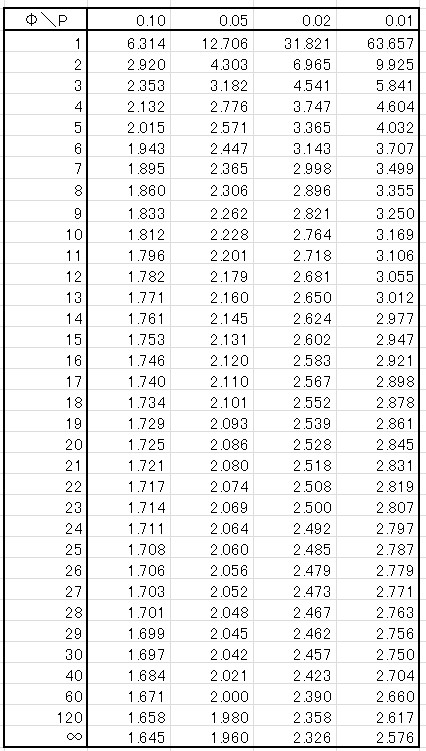
\[t(Φ,α)=t(15,0.05)=2.131\]

※\(Φ\)は自由度を表し、サンプル数-1 の数値のになります。

\[\bar{x}+t(Φ,0.05)×\sqrt{\frac{V}{n}}=30+2.131×{\sqrt{ \frac{3} {16}}}　≒31.60\]

\[\bar{x}-t(Φ,0.05)×\sqrt{\frac{V}{n}}=30-2.131×{\sqrt{ \frac{3} {16}}}　≒28.40\]

よって信頼区間は、28.40～31.60

\[\]

この結果を見てみると、t分布で求めた信頼区間の方が正規分布表から求めた信頼区間(28.53～31.47)より、わずかに範囲が広いことが分かります。

これは、標本データの不偏分散では母標準偏差を100%正確には見積もれないためです。

\[\]

⑦区間推定の精度を上げるデメリット

QC検定では区間推定の信頼度を95%にすることが多いのですが、信頼度は高いほうが良いですよね？

なぜ信頼度を99%に設定しないのか理由を考えてみましょう。

「⑤正規分布の区間推定」の問題を信頼度を99%で解いてみます。

\[\]

問）母分散\(σ^2=3^2\)とわかっている母集団から、16個のサンプルを抽出した。その時の平均値は30だった。信頼度99%で母平均の信頼区間を求めよ。

信頼度が変わったので「PからKpを求める表」より\(\frac{α}{2}\)=\(\frac{0.01}{2}\)=0.005　なので、

\[Z(\frac{α}{2})=2.576\]

よって、信頼区間の上限と下限は

\[\bar{x}+Z(\frac{α}{2})×\frac{σ}{\sqrt{n}}=30+2.576×\frac{3}{\sqrt{16}}=31.932\]

\[\bar{x}+Z(\frac{α}{2})×\frac{σ}{\sqrt{n}}=30-2.576×\frac{3}{\sqrt{16}}=28.068\]

よって信頼区間は28.07～31.93

信頼度95%の信頼区間が28.57～31.47ですから、信頼度99%では信頼区間が広がっています。

このように「データ数が同じ場合」は、信頼度を上げると信頼区間も広がります。

重要なのは、「信頼度をあげると信頼区間が広がる。信頼度がどの程度必要なのか」を自身で考えて設定することです。

\[\]

補足説明のため、具体的な例を考えてみます。

月のおこずかいが3万円のAさんがいます。家計を管理しているのはBさんで、Bさんの気分次第でおこずかいは変動します。

信頼度95%では2.5万円～3.5万円　の範囲内ですが、信頼度99%では1万円～5万円です。さて、月の予算を立てるにはおこずかいを何円と見積もればよいでしょうか？

\[\]

平均値が3万円だから、予算を3万円にすれば良いかもしれません。

しかしそれでは足りない月と余裕がある月が半分ずつの確率で生じるのでへそくりは増えません。

へそくりを確実に増やすには、信頼度99%で考え、月1万円で生活をやりくりすれば問題なさそうです。

しかし月1万円では一日333円しか自由に使えるお金がありません。それではストレスが溜まりそうです。

そこで、信頼度95%の下限である2.5万円を基準にします。

確かに信頼度は99%より落ちますが、そもそも信頼度99%では、月のおこずかいが1万円以下になる確率は200か月に一回の確率です。（両側確率のため）

そんな低確率を基準にするのは心配性が過ぎるかもしれません。

信頼度95%でも2.5万円を下回る確率は40か月に一回の確率だからです。（両側確率のため）

\[\]

こんな感じで、実践的な計画の立るときに推定は効果を発揮します。

\[\]

まとめ

①QC検定2級の点推定はモーメント法を使う

②母平均＝標本平均とは限らない

③区間推定は母平均がのありそうな範囲を推定すること

④信頼区間は両側確率が等しくなるように設定する

⑤正規分布の区間推定は、確率\(α\)の半分の値で正規分布表を使う

⑥\(t\)分布の区間推定は、確率\(α\)の値で\(t\)表を使う

⑦信頼度を上げると信頼区間が広がる。適切な信頼度の設定が重要

\[\]

以上、今回は少し長かったですが、平均値の推定について学びました。

次回は、標準偏差の推定について勉強しましょう！

⇒オススメ書籍はこちら

⇒サイトマップ