(新)QC7つ道具
公開日2020年11月3日 最終更新日 2021年9月19日
みなさんこんにちは、michiです。
前回の記事では、信頼性工学について学びました。
今回は(新)QC7つ道具について学んでいきましょう。
実践で使えるものも多いのですが、今回はQC検定2級対策ということで、要点を絞って解説していきます。
キーワード:「数値データ」「言語データ」「QC7つ道具」
目次
①QC7つ道具とは
QC7つ道具とは、文字通り7つのQC(Quality Control)に使われる手法です。
中でも新QC七つ道具は言語データの解析・分析に使用されます。
この記事説明するのは、以下の9つの手法になります。
- パレート図:問題の影響度を可視化
- ヒストグラム:データを柱状図で表現
- 親和図法:言語データの分類
- 連関図法:因果関係や要因の相互関係の可視化
- 系統図法:系統的に具体的な実施段階のレベルに展開
- マトリックス図法:二元素の交点に関連の有無や度合いを表示
- アローダイヤグラム:計画の進捗と管理
- PDPC法:予め対応策を検討し、望ましい結果にする
- マトリックス・データ解析法:マトリックス図における要素間を定量化
\[\]
9つもありますが、新QC7つ道具は③~⑨の7つになります。
上の9つの中で数値データを扱うものは、①パレート図、②ヒストグラム、⑨マトリックス・データ解析法の3つになります。
それでは早速、一つずつ見ていきましょう。
\[\]
②パレート図
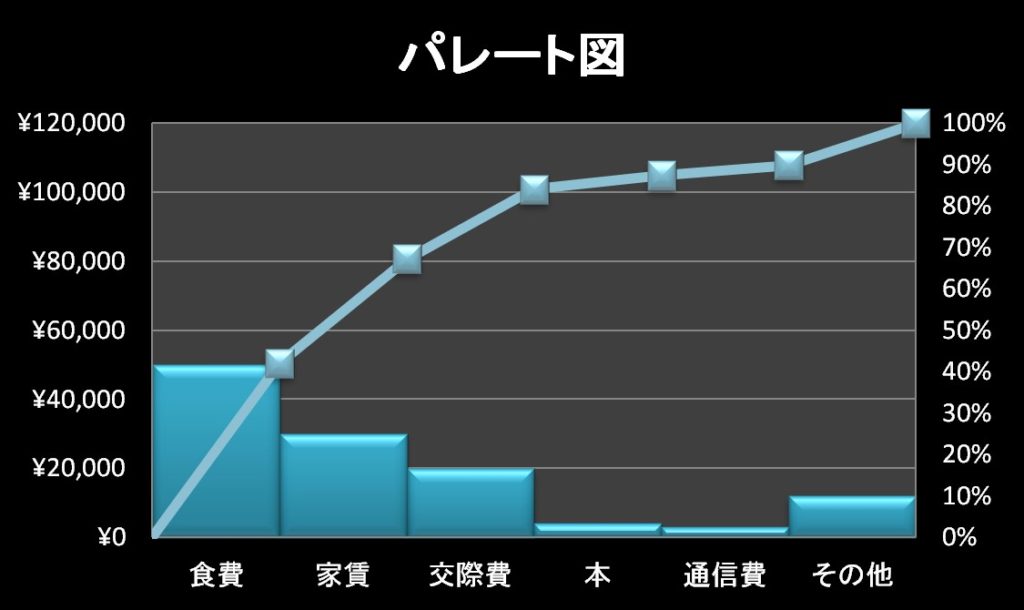
パレート図は、棒グラフと折れ線グラフを組み合わせた複合グラフです。
下の図のような形になります。
\[\]
パレート図には次の特徴があります。
- 棒グラフは左から大きい順に並べる
- 一番右に「その他」が来る
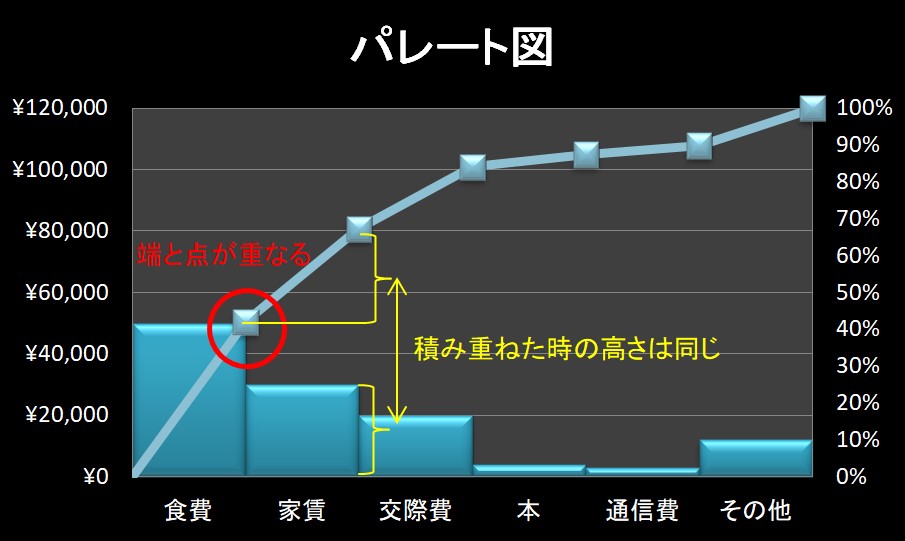
- 棒グラフの右上端に折れ線グラフの点が来る
- 縦軸を揃えることで、データの比較が明確になる
\[\]
パレート図を使うことで、何の項目が全体にどの程度影響を与えているのかが分かりやすくなります。
その結果、何を優先して改善すべきか、何をどうすれば全体がどのように変化するかを見積もったり、比較評価することができます。
\[\]
例えば次の二つのパレート図を見てください。
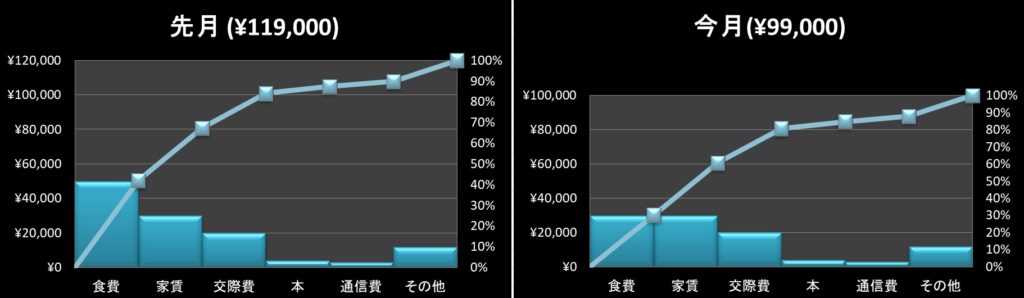
これは、Aさんの先月と今月の支出を表します。
Aさんはオートファジーダイエットを始めてから、晩御飯を食べなくなりました。
そのため、先月と今月を比較すると、棒グラフの高さから食費の支出が減っていることが分かりました。
この時、二つのグラフの縦軸を揃えることで、全体の比較が容易になります。
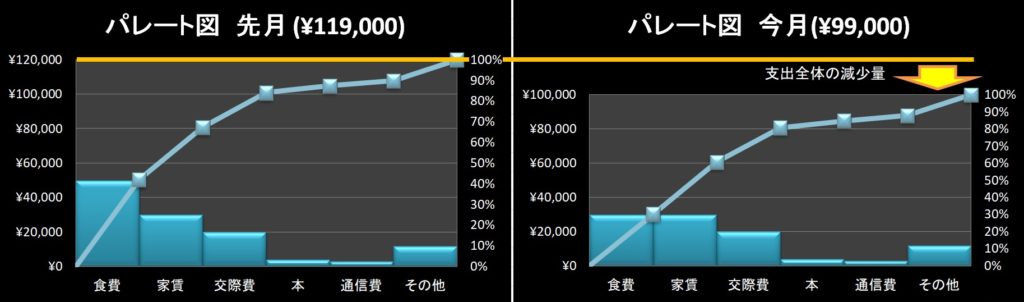
※縦軸を揃えるときは絶対値(上の例では左軸:金額)を揃えます。
相対値(上の例では右軸:%)で揃えても、変化量が見えないからです。
\[\]
③ヒストグラム
ヒストグラムは、縦軸にデータ数(度数)、横軸にデータの数値を取り、柱状図で表したものです。
※ヒストグラムですので、間違えないようにしましょう。
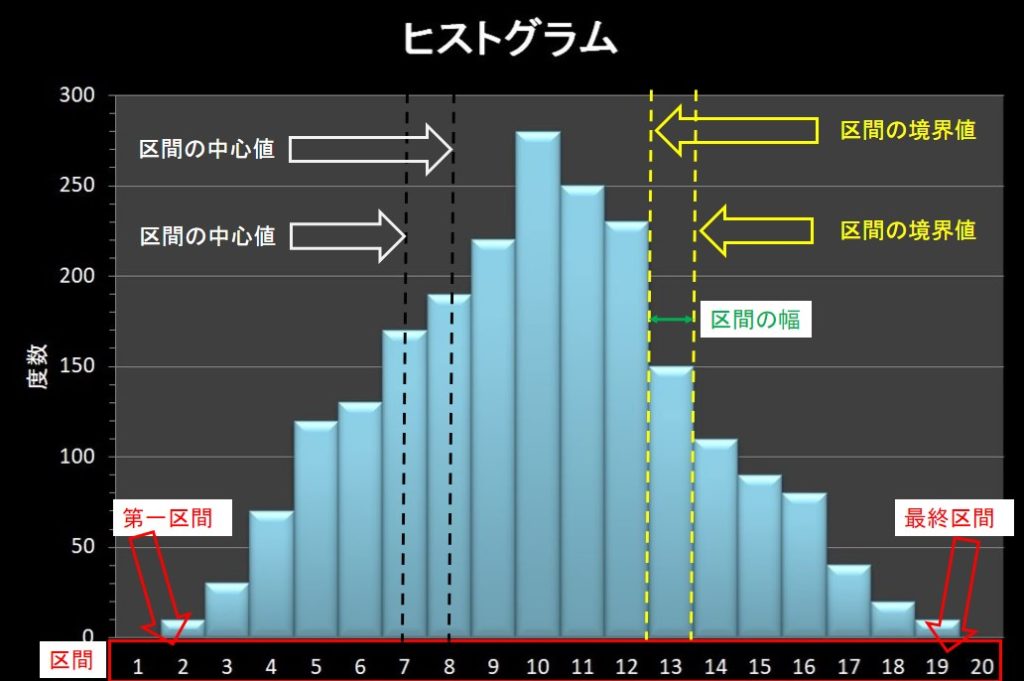
図の書き方は「実践編」でまとめようと思います。
ひとまず、図を見ながら次の用語を覚えましょう。
- 区間:柱状図の基本単位。級、クラスともいう
- 区間の境界値:区間と区間の境界の値
- 区間の幅:区間の境界値の差分。
- 区間の中心値:ある区間の中心に位置する値
- 第一区間:データの最小値がある区間
- 最終区間:データの最大値がある区間
※③区間の幅は、ヒストグラム内の区間の幅はすべて同じになるように設定します。
\[\]
ヒストグラムは、工程能力指数や管理図と組合せて使うことが多いです。
作成したヒストグラムに仕様値などの境界値を加えるなどして、仕様に対する分布のばらつきを可視化し、わかりやすく表現します。
この「ヒストグラムー工程能力指数」の組合せは、QC検定でも頻出になります。
\[\]
また、ヒストグラムはその形状から、管理状態の分析にも使われます。
以下の図とその特徴を覚えましょう。



\[\]
1)一般型:工程が管理された状態の時の分布です。
基となるデータの特性にもよりますが、基本的には左右対称な形になります。
2)離れ小島型:異なる種類のデータが混在している可能性があります。
層別するなど、データのまとめ方を再検討しましょう。
3)絶壁型:規格値を満たしていない製品を取り除いた可能性があります。
分布の中心をずらしたり、ばらつきを抑える処置が必要になります。
4)歯抜け型:測定方法の誤りや区間の設定ミスの可能性があります。
5)二山型:離れ小島型と同様に、異なる種類のデータの混在が疑われます。
※層別:同じグループ(属性)毎にわけること
\[\]
以上がQC7つ道具のパレート図とヒストグラムになります。
数値データを扱う定量的なデータ分析ではよく使うので、覚えましょう。
それでは、新QC7つ道具について学んでいきましょう。
\[\]
④親和図法
親和図法は、事実や意見、発想などの言語データを親和性によって統合した図をつくり、全体像を把握するために使われます。

\[\]
上の例では、「リンゴ、なし、ぶどう」が果物という親和性をもって、一つのグループとなっています。
「小麦、玄米、とうきび」も穀物という親和性を持って、グループになっています。
そして、「果物」と「穀物」は「食べ物」という親和性をもって同じグループに属しています。
\[\]
簡単な例題ではありましたが、会社の研修などでこのような「ブレーンストーミング」をした経験がある人も多いのではないでしょうか。
「ブレーンストーミング」では、いろいろな意見を最後いくつかのグループでまとめていきます。
この時同じような(=親和性の高い)意見を一つのグループにします。
「ブレーンストーミング」は、親和図法のひとつの例になります。
\[\]
この親和図法は、日常生活でも大いに役立つと私は考えます。
私が読んで参考になった本「イシューからはじめよ」や「考える技術・書く技術」に書かれている「ピラミッド構造」で考えるとは、まさしくこの親和図法であると考えるからです。
日常生活でも、いくつかのデータから「それってどういうこと?」を要約できるようになりたいですよね。
\[\]
⑤連関図法
連関図法は、「原因ー結果」や「目的ー手段」などの因果関係や要因相互の関係を明らかにすることで問題解決をする手法です。

ビジネス系YouTuber さんが「マインドマップ」を使われているのを見たことがある人も多いと思います。
これも先ほど紹介した「イシューから始めよ」や「考える技術・書く技術」で書かれているピラミッド構造を使って考える方法になります。
「イシューから始めよ」では、「Whyの並べ立て」と表現されています。
\[\]
また、前回の記事「信頼性工学 2」で紹介したなぜなぜ分析を思い出してみても良いです。
テーマ(トップ事象)に対し「why」を繰り返すことで、本質的な原因を論理的に見つけます。
\[\]
抽象的な説明だったので、ここで具体例を挙げてみましょう。

上の例では、「筋肉量が低下」した要因を「Whyの並べ立て」で考えました。
それぞれの要素を分析すると・・・
現在断食を継続中のため、「空腹16hour」は取り除けそうにありませんが、「蛋白質不足」は、断食で夕食で取れなくなった分のたんぱく質を朝食に取れば解決しそうです。
そのほかにも、最近残業ばかりで「忙しい」のも筋肉量減少の要因になりそうですね。
このように要因を分析することで、対策がしやすいもの、対策が難しいものを抽出し、有効な手段を選択することができます。
\[\]
⑥系統図法
系統図法は、方策を系統的に具体的な実施段階のレベルに展開し、最適な手段を見つける手法です。

「系統的に」とは、「目的⇒手段」を繰り返すと覚えましょう。
目的に対しそれを達成できる手段を考え、その手段の実現を目的として、さらに達成できる手段を考え・・・と繰り返していきます。
最終的に得られた手段をマトリックス図法などを用いて評価し、目的を達成するための手段を決めます。
\[\]
例えば、次の例題を考えてみましょう。

この例では、筋肉量を増やす方法を系統図法で考えています。
筋肉量を増やす手段として、「筋トレをする、プロテインを飲む、…」などが挙げられています。
次に筋肉量を増やす手段である「筋トレをする」を目的として、それを実現する手段を考えます。
すると、「筋トレをする」を目的とする手段として、「ジムへ行く、自宅トレをする」が考えられます。
最終的に「ジムへ行く」を手段としたときに、マトリックス図法を用いて、ジムを比較します。
\[\]
図ではジムA、ジムB、ジムCが挙げられています。
総合評価ではジムAが良さそうですので、ジムAで筋トレをし、筋肉量を増やす目的を達成するようにします。
ただし、ジムCにしかない設備がなければ目的を達成できない場合は、コストや距離があろうとも、総合評価が低くとも選択肢はジムCになります。
\[\]
さて、よく聞く「手段が目的になってしまう」という話は、この目的ー手段を系統的に判断できなくなった状態になります。
先の例題の場合、本来の目的である「筋肉量を増やす」まで系統的に遡ることができず、「ジムに行く」という手段が目的のままで終わってしまう状態です。
ジムへ行くことが目的になってしまったので、つらい筋トレはやらずに、友達と談笑して終わってしまう…なんてことになりかねません。
\[\]
⑦マトリックス図法
マトリックス図法は、対になる二つの要素を行と列に分けて配置し、二つの要素の交点にその関連の有無や関連の度合いを表示する手法です。

関係がありそうな要素同士を抽出するときや、層別をするときに有効となります。
マトリックス図法では、縦軸に比較したいもの同士(A、B、C)を、横軸に比較項目(実現性、有効性、コスト、…)を並べた表を作成します。
作成されたマトリックス図を基に、選択肢を決めていきます。
\[\]
マトリックス図法で重要なのは、以下の二点です。
- 総合評価が高いからといって最適解になるとは限らない
- 比較項目はMECE(ミッシー)で並べる
\[\]
①「総合評価が高いからといって最適解になるとは限らない」
それでは、次のマトリックス図を見て、どれがベストな方法
か考えてみてください。

いずれも「×」があります。
総合評価では、「◎」が一番多いAがベストで、「◎」が一つもないCはワーストになりそうです。
・・・ではもう少し考えてみましょう。
\[\]
確かに、Aは「実現性」と「コスト」で「◎」の評価を得ています。
しかし「有効性」が「×」です。
つまり、コストパフォーマンスが良く実現性の高い、有効性のない方法ということです。
何か達成するための方法なのに、有効性がない時点でアウトですよね!?
\[\]
では次に「有効性」が「◎」のBはどうでしょうか?
これなら「コスト」もほどほどに良さそうです。
しかし「実現性」が「×」です。
つまり、ほどほどのコストで有効性の高い、実現不可能な方法ということです。
どんなに有効性が高くても、実現できないのでは元も子もないですよね。
\[\]
では、最後に「有効性、実現性」が「〇」、「コスト」が「×」のCはどうでしょうか?
コストは高くつきますが、他選択肢と比較して、実現可能で有効性がほどほどにあるものと評価できます。
コストを払ってでも解決すべき課題であれば致し方ありませんね。
\[\]
②「比較項目はMECE(ミッシー)で並べる」
例えば、次の表をみて違和感を感じないでしょうか?

麻婆豆腐の味が「×」なんてありえない!
・・・ということではありません。
このマトリックス図では、料理の分類と料理名が混在しています。
うどんは和食の分類に、麻婆豆腐は中華の分類に入るはずです。
比較したい項目が「料理の分類」なのか「料理名」なのかを統一する必要があります。
なぜなら、確かに麻婆豆腐は味が「×」かもしれませんが、総合評価では「中華」という選択肢が選ばれる可能性が高いからです。
「中華」で「麻婆豆腐」を食べなければ良いだけの話なのです。
\[\]
さて、説明が後回しになりましたが、MECEとは、「Mutually Exclusive, Collectively Exhaustive」のことです。
日本語にすると「もれなく・ダブりなく」という意味です。
もれやダブりがあると、適切な評価が難しくなります。
上の例題でも、「麻婆豆腐」は「中華」の分類ですから、「ダブりのある」マトリックス図でした。
\[\]
MECEという言葉自体は、最近徐々に浸透してきたと思います。
ご存じの方も多いのではないでしょうか。
MECEの考え方はマトリックス図法に限らず、日常生活や仕事にも使える基本的な考え方なので、意識してみましょう。
\[\]
⑧アローダイヤグラム
アローダイヤグラムとは、計画を進めるうえで必要な作業の順序を矢印→と結合点○を用いた図を使って表す手法です。
効率的な日程計画の作成と計画の進捗を管理する手法です。
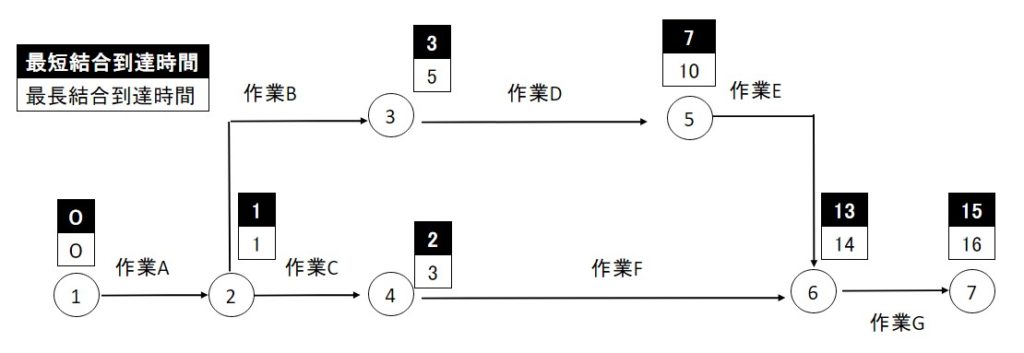
「ダイヤグラム」と聞くと、電車のダイヤグラムを思いつく人も多いと思います。
まさしくその「ダイヤグラム」で、アロー(矢)のついたダイヤグラムなので、アローダイヤグラムとなります。
矢(印)の部分には実作業を、結合点○の中には作業の順番に当たる数字を書きます。
実用的には、追加で最短結合到達時間と最長結合点到達時間を書くことで、計画の幅を見積もりやすくなります。
\[\]
具体的な例を考えてみましょう
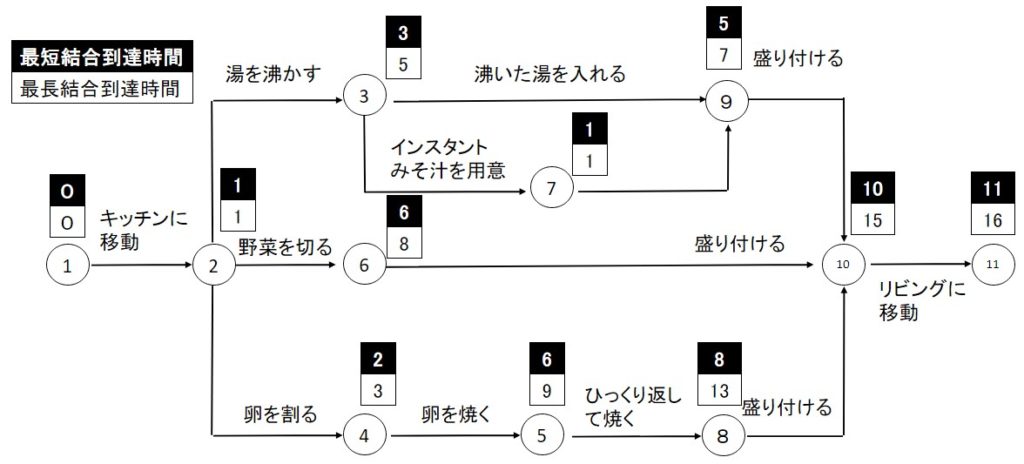
この例では、朝起きてから朝食を準備する様子をアローダイヤグラムで表しています。
始点では、最短結合到達時間と最長結合到達時間はともに0で始まっています。
その後、キッチンへ1分で移動した後は、「湯を沸かす⇒卵を割る⇒卵を焼く⇒・・・」と作業を進めていきます。
この時、例えば、「野菜を切る」作業では6分~8分の作業の幅を見積もっていることが分かります。
\[\]
作業を進めていくと、「盛り付ける」で⑩に終結されています。
この例では目玉焼きを作る作業がボトルネックになっています。
そのため「盛り付ける」が終わる時間(⑩に到達する時間)は、目玉焼き完成の8~13分に+2分をした、10分~15分の幅で見積もられています。
※+2分は「盛り付ける」に要する時間です。
\[\]
このようにアローダイヤグラムでは、「作業の手順」、「ボトルネック作業の見極め」、「作業完了時間の見積もり」が容易にできます。
\[\]
⑨PDPC法
PDPC法とは、「プロセス決定計画図(Process Decision Program Chart )」のことです。
目標達成のための実施計画が想定されるリスクを回避して、目標に至るまでのプロセスをフロー化した図のことです。
ポイントは、フロー図は時系列または対策順に並んでいることです。

PDPC法には、逐次展開型PDPC と 強制連結型PDPCの二種類があります。
逐次展開型PDPCとは、現在の状態と目標とする状態を明確にし、その進展過程で発生する状態を事前に予測しながら、その時点での方策を逐次に計画して目標を達成する手法です。
\[\]
強制連結型PDPCとは、初期状態と最終の事態を多方面から想定し、そのプロセスやケースを様々に予測し、重大な事態を避けるときに使用されます。
例えば、災害による二次災害、三次災害をどのように防ぐかを考える場合が、この強制連結型PDPCに該当します。
\[\]
それでは、逐次展開型PDPCの例題として、健康診断を良い結果にするための方法を見てみましょう。

このPDPCでは、まず初めに健康診断の日程を確認します。
その次に断食で体重を減らすのですが、うまく体重を減らせない場合は、エナジードリンクの飲む量を減らすことで、対策をします。
次のステップでは筋トレで筋肉量を増やすのですが、うまくいかない場合は、プロテインを飲み、それでもダメな場合は、強度の高いトレーニングをします。
最後に健康診断前日は無理をせず、早く寝ます。
簡単な例ではありましたが、方法が対策順になっていることが分かります。
「健康診断前日は早く寝る」を最初に持ってくると、時すでに遅し、もう何もできませんよね。
\[\]
⑩マトリックス・データ解析法
マトリックス・データ解析法は、主成分分析とも呼ばれる多変量解析の手法の一つになります。
マトリックス図法とは異なり、数値データを扱います。
新QC7つ道具では、唯一数値データを扱う手法となります。

マトリックス図法では「◎、〇、△、×」などの定性的な表現で関係性を表していました。
マトリックス・データ解析法では、比較項目を数値化することで、定量的に表現します。
定量的な評価をすることで、人による認識の違いの影響を受けません。
つまり、「◎、〇、△、×」などの定性的な表現は、人によって判断基準が異なる可能性がありますが、定量的な表現(例:\3,000/月)は客観的な事実なので、誰でも同じ情報を共有できるわけです。

\[\]
マトリックス・データ解析法の属する多変量解析は、QC検定2級の出題範囲を逸脱しているので、今回は紹介しません。
QC検定2級では、「新QC7つ道具では唯一数値データを扱う手法」とだけ覚えておきましょう。
\[\]
まとめ
①覚えるべき(新)QC7つ道具は、全部で9つ
②パレート図は、棒グラフと折れ線グラフを組み合わせたグラフ
③ヒストグラムは、度数とデータを柱状図で表現
④親和図法は、親和性のある者同士を結合した図
⑤連関図法は、因果関係や要因相互の関係を明確にする
⑥系統図法は、方策を系統的に具体的な方法で考える
⑦マトリックス図法は、二つの要素の関係性を定性的に評価
⑧アローダイヤグラムは、日程計画や進捗の把握に使用
⑨PDPC法は、事前に考えられるリスクを避け、プロセスをフロー図化
⑩マトリックス・データ解析法は、マトリックス図法を定量的に表現
\[\]
今回は長い記事となってしまいました。
しかし、今回取り上げた9つの手法はいずれもQC検定で出題されやすいです。
QC検定で必要な知識は今回取り上げましたが、実務への応用は実践編でまとめていこうと思います。
次回は品質管理の実践分野として、専門用語を学んでいきましょう。
\[\]















[…] 次回はQC7つ道具について勉強していきましょう! […]
[…] 前回の記事では、新QC七つ道具を学びました。 […]