公開日2020年5月1日 最終更新日 2022年7月9日
みなさんこんにちは、michiです。
前回までは、正規分布、\(χ^2\)カイ二乗分布、F分布、t分布といった統計量について勉強しました。
今回はその統計量を使った「検定」とは何か?について学んでいきましょう。
キーワード「帰無仮説」「対立仮説」「両側・片側検定」
目次
①(仮説)検定とは
(仮説)検定とは、「サンプリングした標本から統計量を計算し、仮説の妥当性を判断すること」です。
例えば、サンプリングした標本から平均値の妥当性を評価したい場合は、検定統計量 \(Z\) や \(t\) を使います。
\[\]
具体例を考えてみます。
「サイコロがイカサマ」であるという仮説の妥当性を評価します。
すると、以下の二つの仮説が考えられます。
- 使われているサイコロはイカサマだろう(=普通ではない)
- 使われているサイコロはイカサマではないだろう(=普通)
\[\]
どちらの仮説の妥当性を評価しても「サイコロがイカサマ」か否かの判断ができるのですが、この時、
- 「使われているサイコロはイカサマだろう」とする仮説を帰無仮説
- 「使われているサイコロはイカサマではないだろう」とする仮説を対立仮説
\[\]
といい、帰無仮説を\(H_0\)、対立仮説を\(H_1\)と書きます。
仮説が成り立ってほしくない方を帰無仮説と覚えましょう。
※\(H\) は英語のHypotheis (=仮説)が由来です。
“φ(・ω・。)フムフム…
\[\]
帰無仮説が正しい場合を「帰無仮説を採択する(棄却できない)」といい、帰無仮説が正しくない場合を「帰無仮説を棄却する」といいます。
帰無仮説と対立仮説は表裏一体の関係で、帰無仮説が棄却されたときは、対立仮説が採択されることになります。
\[\]
②検定の誤り
標本から得られたデータを基に、母集団の性質を仮定しそれを検証することを検定といいました。
しかし、検定では誤った判断をすることがあります。
\[\]
例えば、サイコロはイカサマという仮説(帰無仮説)を立て、サイコロを60回投げた場合を考えます
この時、1の目が 12回 出たとします。果たして、このサイコロはイカサマでしょうか?
(。´・ω・)?
\[\]
1の目が出る期待値は10回だけど、まぁ12回くらいならイカサマサイコロではないだろうと判断したとします。
つまり、帰無仮説を棄却(サイコロはイカサマであるという仮説は間違いと判断)したわけです。
でも実は帰無仮説は正しかった(サイコロはイカサマだった)!なんてことがあります。
\[\]
このように、帰無仮説は正しいのに棄却するという誤った判断のことを「第一種の誤り\(α\)(=あわてものの誤り)」といいます。
\[\]
第一種があるということは・・・ そう、第二種の誤り(判断の誤り)もあります。

\[\]
先ほどと同様に、サイコロはイカサマという仮説(帰無仮説)を立て、サイコロを60回投げた場合を考えます。
この時、1の目が 14回 出たとします。果たしてこのサイコロはイカサマでしょうか?
イカサマダ! (# ゚Д゚)つ〃∩ ゴルァ ゴルァ ゴルァ
\[\]
1の目が出る期待値は10回なのに、14回でたからイカサマサイコロだろうと判断したとします。
つまり、帰無仮説を採択(サイコロはイカサマであるという仮説が正しいと判断)したわけです。
\[\]
でも実は帰無仮説は間違ってた(サイコロは普通ではないとはいえない)!なんてこともありえます。
このように、帰無仮説は間違っているのに採択するという誤った判断のことを「第二種の誤り\(β\)(=ぼんやりものの誤り)」といいます。
\[\]
これを表にまとめると下のようになります。

通常QC検定では、この第一種の誤り\(α\)を5%(まれに1%)で見積もります。
誤りが5%ということは、20回に1回は誤った判断をしてしまう精度で、標本から母集団を見積もりましょうということです。
統計的な検定では一般的に帰無仮説を5%とすることが多いです。
(´・∀・`)ヘー
\[\]
③どっちのリスク?
帰無仮説は正しいのに棄却してしまう第一種の誤り\(α\)と、帰無仮説は間違っているのに採択してしまう第二種の誤り\(β\) があることを学びました。
\[\]
さて、間違った判断をしたということは、誰かがその損害を受けることになります。誰でしょうか?
(。´・ω・)?
サイコロの例ではわかりにくいので、あなた(=生産者)が製品Aを客(=消費者)に売る場合を想定してみます。
\[\]
あなたは製品Aを合格品なのに、誤って不合格品として廃棄したとします。
これは、製品Aが合格という帰無仮説を棄却したことに相当します。
本来売れるはずの製品Aを廃棄するわけですから、あなた(=生産者)が損をします。
このように第一種の誤りを別名「生産者のリスク」といいます。
\[\]
では逆に製品Aは不合格品なのに、合格品として売った場合はどうでしょう?
これは、製品Aは不合格なのに帰無仮説を採択した(製品Aを合格品と判断した)ことに相当します。
\[\]
あなた(=生産者)は製品Aを売っているわけですから、あなたは損をしていません。
しかし、客(=消費者)は不良品を買わされたので損をします。
このように第二種の誤りを別名「消費者のリスク」といいます。

\[\]
④統計量の概念
第一種の誤りは5%に設定されることが多いと説明しました。
では、実際に帰無仮説を95%の精度で棄却または採択するには、どのように判断すればよいのでしょうか?
(。´・ω・)?
\[\]
サイコロの例に戻って考えてみましょう。
今度は少し多めに600回投げたとします。
すると、通常のサイコロであれば1の目が出る期待値は100回くらいです。
この時、「サイコロの出る目に偏りは無い」を帰無仮説とします。
このときの対立仮説は「サイコロの出る目に偏りがある」です。
\[\]
100回くらいということは、1の目が99回や101回でも問題ないということです。
では、1の目が10回の場合はどうでしょうか?
期待値が100回に対し10回というのは少なすぎますよね。
\[\]
つまり「サイコロの出る目に偏りは無い」という帰無仮説を棄却することができます。
この時の様子は下のグラフです。

※横軸が1の目が出た回数、縦軸が1の目の出やすさを表します。
\[\]
95%の精度でサイコロの出る目に偏りは無いと判断するには、「600回サイコロを投げるテストを100回繰り返し、1の目が出る回数が期待値100回付近の、上位95回の1の目が出る範囲」を決めればよさそうです。
・・・(。´・ω・)?
図示すると下のようになります。
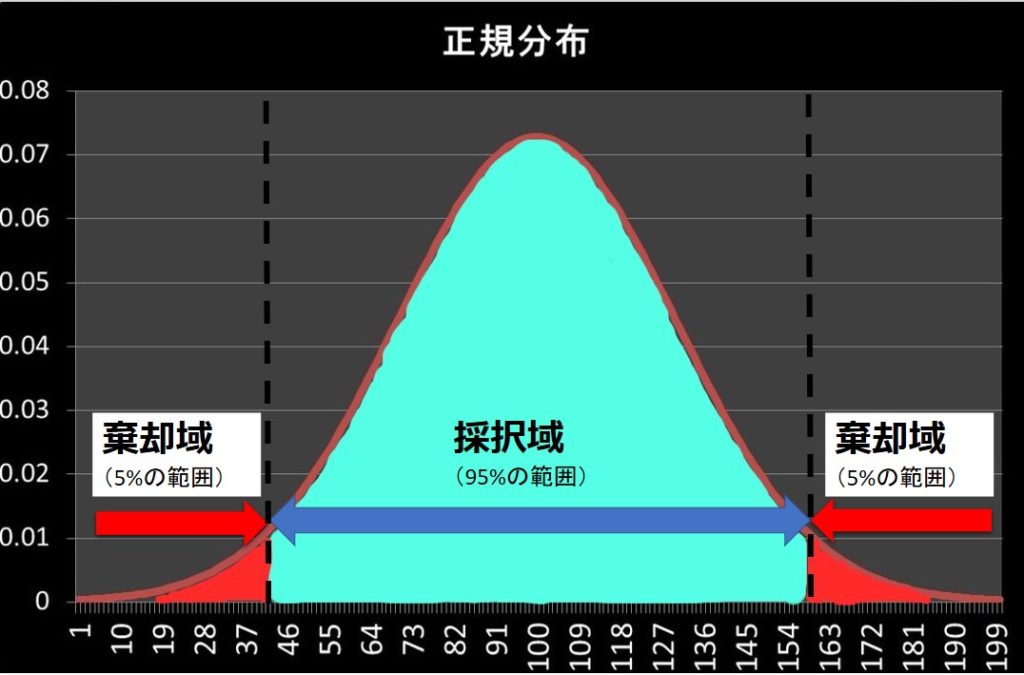
この時の横軸に対し、普通のサイコロ(帰無仮説が成り立つ)であれば95%の確率で出るであろう1の目の出る回数の範囲を採択域。
逆に95%の確率で出ないような1の目の出る回数の範囲を棄却域といいます。
また、棄却域と採択域の境界値を棄却限界値といいます。
\[\]
1の目が棄却域の範囲の回数出た場合、帰無仮説を棄却(対立仮説を採択)します。
また、帰無仮説の棄却域は対立仮説が成り立つ領域(対立仮説が有意)となることも覚えておきましょう。

\[\]
⑤両側検定と片側検定
先ほどの例では、通常のサイコロ(=帰無仮説)か否かを判断するために、グラフの両側に棄却域を設定しました。
これは、期待値付近から離れた領域の1の目の出る回数は、多すぎても少なすぎても普通のサイコロではないと判断するためです。
\[\]
このように、両側に棄却域を設定して検定することを両側検定を言います。
※両側検定では、棄却域は両側にあり、両側の棄却域をあわせて第一種の誤りの範囲とします。
正規分布は左右対称な形なので、両側検定の片側の棄却域の範囲は、2.5%ずつの範囲となります。(両棄却域を合計して5%)
\[\]
では、イカサマサイコロを使われて、1の目が出やすくなった場合を考えます。
この場合も同様に両側検定で考えてもよいのでしょうか?
キョロ(・ω・`Ξ´・ω・)キョロ
\[\]
答えは 「NO」 です。
この場合の帰無仮説は「サイコロの出る目に偏りは無い」で、対立仮説は「1の目が出やすいイカサマサイコロ」 になります。
帰無仮説は同じですが、対立仮説が変わりました。
\[\]
両側検定では、1の目が出る回数が多すぎても少なすぎても「通常ではない」と判断するために、両側に棄却域を設定しました。
もし今回の対立仮説「1の目が出やすいイカサマサイコロ」で両側に棄却域を設定すると、1の目が出にくいほうにも棄却域を設定することになります。
\[\]
1の目が出にくいほうに帰無仮説の棄却域があると、対立仮説である「1の目が出やすいイカサマサイコロ」に対し、「1の目が出にくい場合も有意」になってしまいます。
(*´・ω・)ん?
(; ´◎ ω ◎)んん?
\[\]
少しややこしいですね。
つまり、「1の目が出やすい」という対立仮説に対し、「1の目がでにくい状態にもかかわらず、1の目が出やすいという(対立)仮説は正しい(有意である)」と判断することになってしまうのです。
これは誤った考えですよね。
\[\]
このように、「大きいか(小さいか)を検定」するときに両側に棄却域を設定すると変なことになります。
「大きいか(小さいか)を検定」するときは、帰無仮説の棄却域を片側のみに設定し検定します。
これを片側検定といいます。
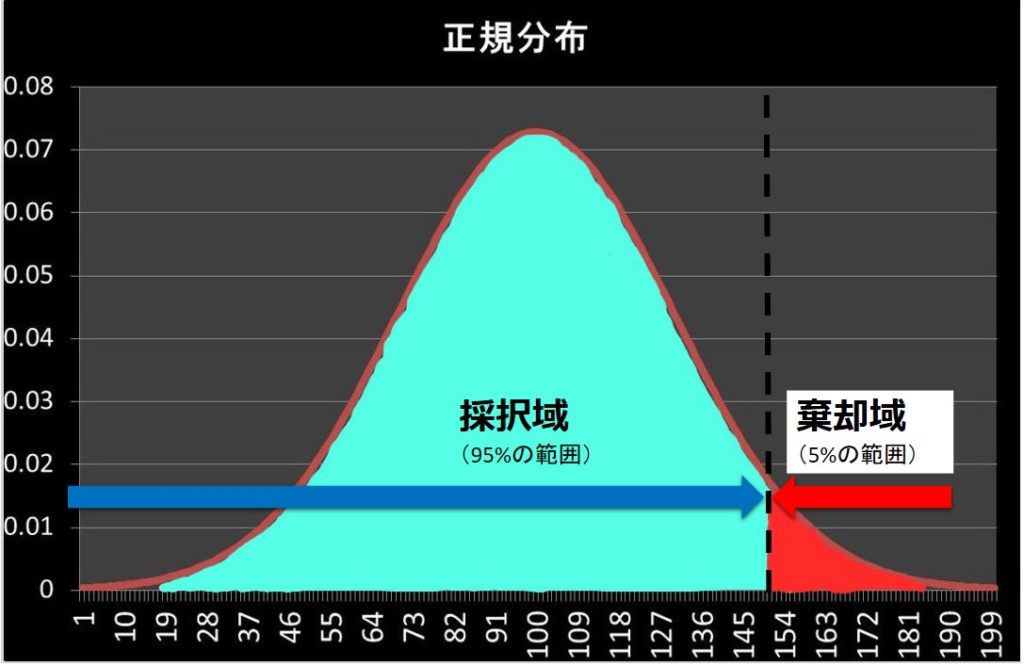
両側検定では、両側に棄却域を設定したのに対し、片側検定では片側のみに棄却域があります。
このため、棄却域と採択域の境界線の位置(棄却限界値)が、採択域側にずれます。
これは、第一種の誤り5%の範囲を片側の範囲のみで確保するためです。
\[\]
まとめ
①検定は仮説の正しさを証明すること
②検定は一定の精度で正しさを判断する
③検定の誤りは「生産者のリスク」「消費者のリスク」ともいわれる
④仮説の正しさは、帰無仮説を棄却できるか否か
⑤仮説を棄却できる範囲は、両側だったり片側だったりする
\[\]
今回は、検定の概念について勉強しました。
次回からは、正規分布、t分布、\(χ^2\)カイ二乗分布、F分布のそれぞれの分布に対しての検定方法について、勉強していきましょう。

















[…] では、どう評価すればよいのか?については、別の記事「検定とは」や各推定の記事で解説します。 […]