検査の種類と方法

公開日2020年9月13日 最終更新日 2022年8月27日
みなさんこんにちは、michiです。
前回の記事ではサンプリングについて勉強しました。
今回は抽出した検査について学びましょう。
キーワード:「検査の種類」「OC曲線」
目次
①検査の種類
検査の種類は主に次の3種類があります。
- 受入検査
- 工程間検査(中間検査)
- 最終検査(出荷検査)
それぞれの説明の前に、検査の目的を考えてみましょう。
検査の目的は、個々の製品に対し「適合(良品)」か「不適合(不良品)」の判定を行い、ロット全体に対して、「合格」か「不合格」の判定を行うこと です。
\[\]
例えば、1 ロット200 個の部品を受入検査したとします。
そのうち198 個は適合品(良品) で、2個は不適合(不良品)だったとします。
何%までの不良品を許容できるかによって答えは変わるのですが、\(P_0=0.2% , P_1=2%\) の場合は、ロット全体が不合格となります。
※詳細は後ほど説明します。
このように、検査したロットの適合品/不適合品の数によって、ロット全体を合格/不合格 と判定することが検査の目的です。
\[\]
さて、少し前置きが長くなりましたが、それぞれの検査について説明します。
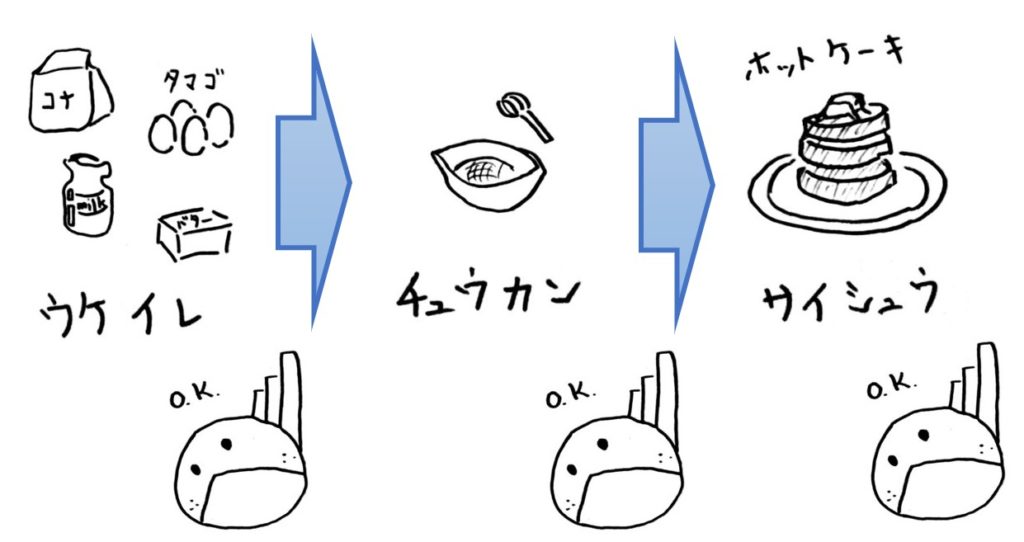
1.受入検査
受入検査は、納品した部品や製品を受け入れても良いかを判定する検査になります。
\[\]
2.工程間検査・中間検査
工程間検査は、製品を製造する途中の工程で検査することになります。
製造の途中で検査をすることで、不良品を作り続けてしまうロスを取り除けます。
\[\]
3.最終検査・出荷検査
出荷検査では、出来上がった製品に対して、品質を満足しているかを検査します。
\[\]
②検査の方法
検査の方法は、主に次の3種類があります。
- 全数検査
- 無試験検査・間接検査
- 抜き取り検査
それぞれについて、説明します。
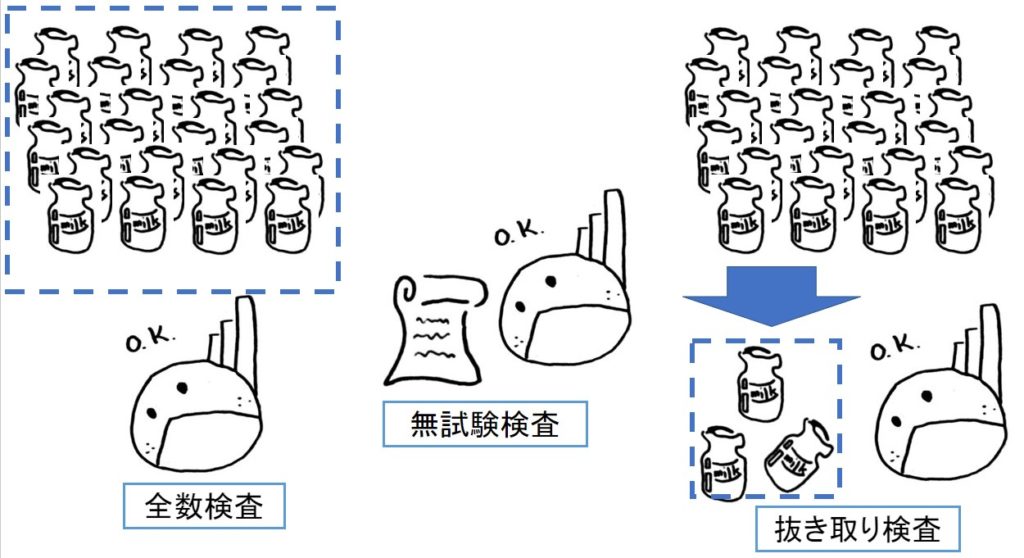
1.全数検査
全数検査は、ロット内のすべての製品を検査する方法です。
人の命に関わるような車などの製品や、ブランド品などの非常に高付加価値の商品に対して実施されます。
全数検査は手間がかかり、コストが割高になる特徴があります。
\[\]
2.無試験検査・間接検査
無試験検査・間接検査は、製品保証書や成績書などの書類だけで品質を担保する検査です。
不適合品がほぼないと考えられる製品や、不適合品があっても受入側の品質に影響がない場合の製品、そもそも受入側で検査する設備がない場合などで、実施されます。
例えば、プロテインやサプリメントには、含有成分の情報が記載されていますが、普通の使用者は成分分析機など持っていませんから、無試験検査になるわけです。
ややこしいですが、無試験検査・間接検は、検査しない検査になります。
\[\]
3.抜き取り検査
抜き取り検査は、検査ロット(母集団)からサンプリングし、そのサンプルに対して検査をします。
検査の結果から、不適合品の数によって、検査ロット全体(母集団)の合否判定をします。
この時、検査ロットから抜き取るサンプルの大きさ \(n\) と、検査ロットを合格と判定する合格判定個数(最大不適合品数)\(c\) の組みあわせを「抜き取り検査方式」といいます。
※不適合品が合格判定個数\(c\) 個以下なら、ロットは合格となります。
\[\]
③OC曲線(検査特性曲線)
これまで、検査の方法と種類について学びました。
QC検定ではOC曲線という概念を学ぶ必要があります。
OC曲線は、ある不適合品率のロットが合格する確率を表した曲線になります。
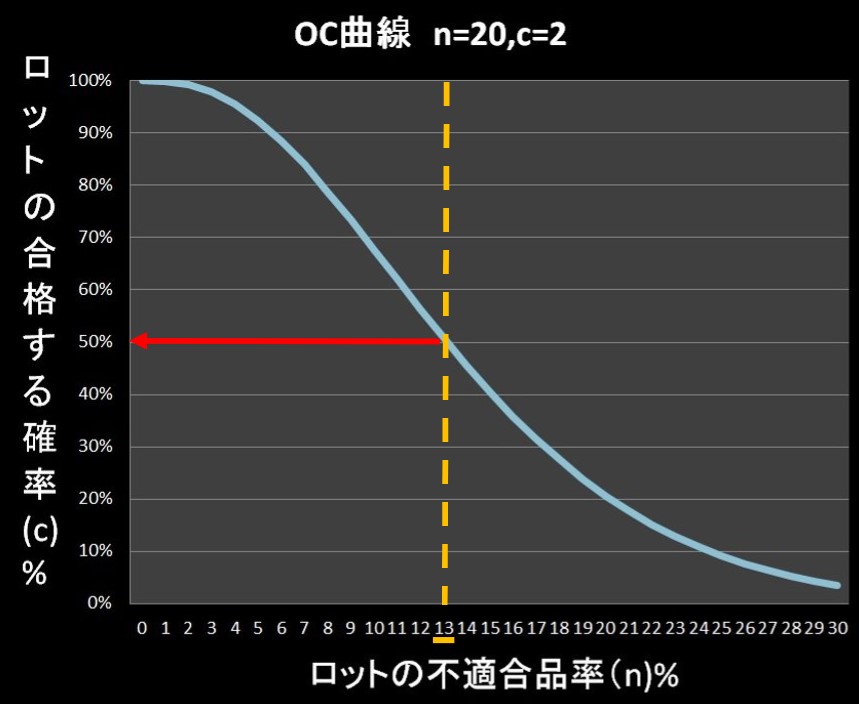
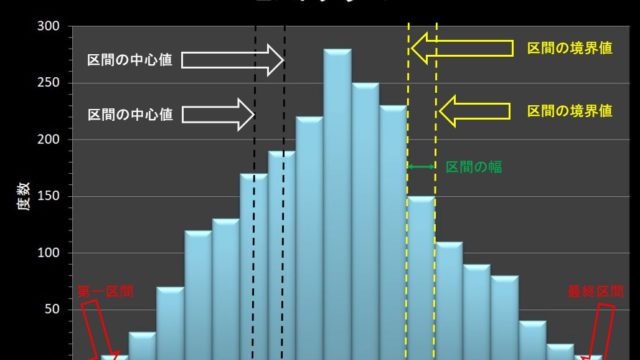
実際には、下図のようになります。(サンプル数\(n=20\),合格判定個数\(c=2\)の場合)
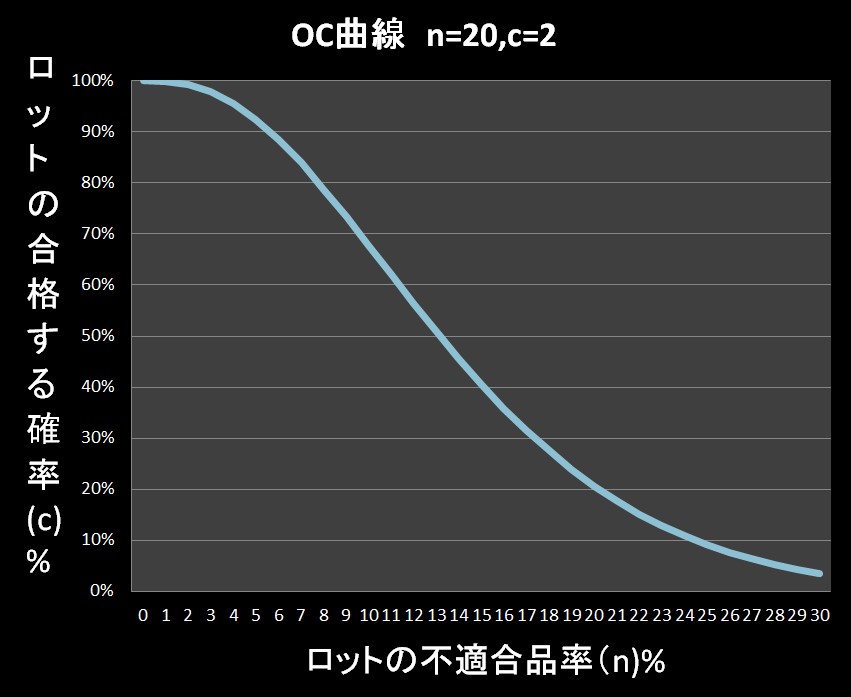
横軸が「ロットの不適合率\((n)%\)」で、縦軸が「ロットの合格する確率\((c)%\)」を表します。
ロットの不適合品率が0%、つまり不適合品が発生しなければ、ロットは当然、100%合格になります。
逆に、「ロットの不適合品率」が上昇すれば、合格判定個数を上回る数の不適合品が抽出される確率が上がるため、「ロットの合格する確率」は小さくなります。
\[\]
具体的にどのように見るかというと、「ロット不適合品率」に対応する、「ロットの合格する確率」を読み取るだけです。
下図の例では、「ロット不適合品率=13%」のとき、「ロットの合格する確率=50.8%」となります。
※サンプル数\(n=20\),合格判定個数\(c=2\)の場合
\[\]
このOC曲線には他にも特徴があります。
覚えておくのは、以下の特徴です。
- 合格判定個数\(c\)が同じ条件で、サンプル数\(n\) が増えるほど、傾きは急になる
- サンプル数\(n\)が同じ条件で、合格判定個数\(c\) が減るほど、傾きは急になる
\[\]
①の意味としては、ロットを合格と判定する合格判定個数\(c\) は変わらないのに、サンプル数\(n\) が増える状態です。
つまり、枠(合格判定個数\(c\))は同じなのに、応募者(サンプル数\(n\))が増えるような状態ですから、より厳しい試験になります。
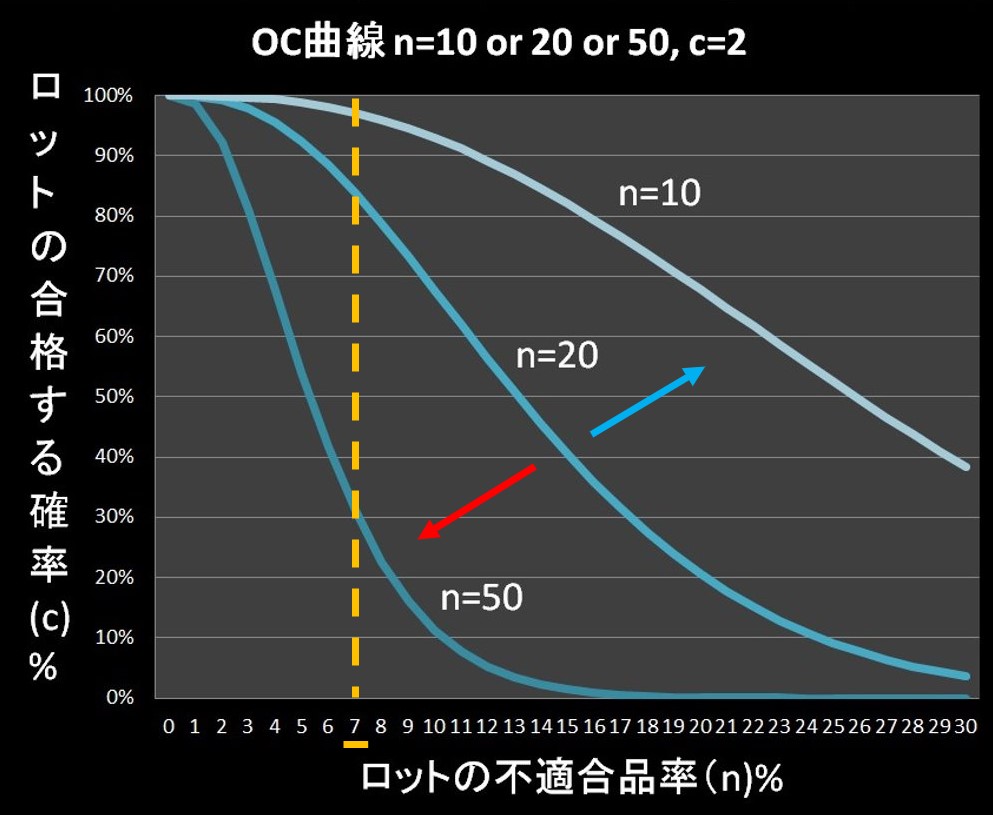
同じ「ロットの不適合品率」でみると、サンプル数\(n\)が増えるほど、「ロットの合格する確率」は下がっています。
\[\]
次に②の意味ですが、サンプル数\(n\) は変わらないのに、ロットを合格と判定する合格判定個数\(c\) が減る状態です。
つまり、応募者(サンプル数\(n\))は同じなのに、枠(合格判定個数\(c\))が減るような状態ですから、より厳しい試験になります。
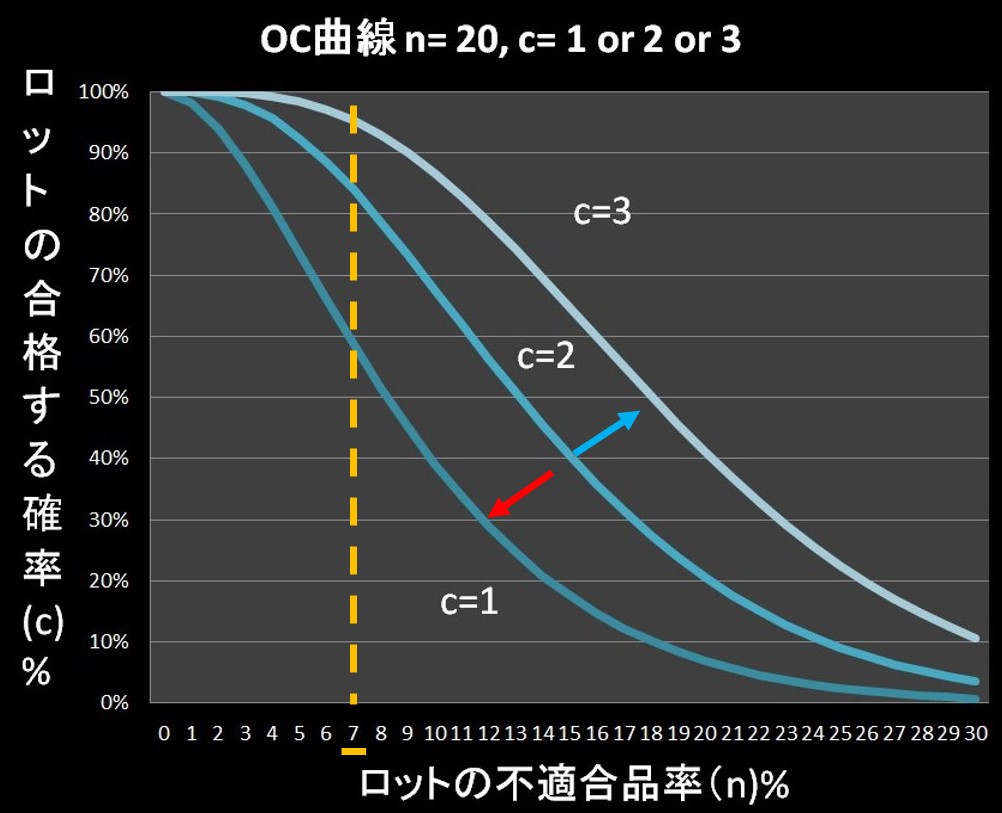
同じ「ロットの不適合品率」でみると、合格判定個数\(c\)が減るほど、「ロットの合格する確率」は下がっている。
\[\]
OC曲線はQC検定に割と出てくるグラフです。
意味や見方を知っていれば怖くないのですが、初見では強敵です。
\[\]
④計数基準型抜き取り検査
さて、「②検査の方法」で紹介した抜き取り検査方式について詳しく説明します。
抜き取り検査の代表的なものに、計数基準型抜き取り検査というものがあります。
計数基準型抜き取り検査とは、生産者のリスク\(α%\) と、消費者のリスク\(β%\) を一定になるように保護する検査のことです。
(。´・ω・)?
重要なことは、生産者のリスク\(α%\) と、消費者のリスク\(β%\) を保護できるような検査をするために、サンプル数\(n\) と合格判定個数\(c\) を決めることです。
その際に「JISZ 9002 計数基準型1回抜き取り検査表」を使用します。
※一応リンクは貼りましたが、文字化けして読みづらいので、以下を参照してください
本番では巻末についてきます
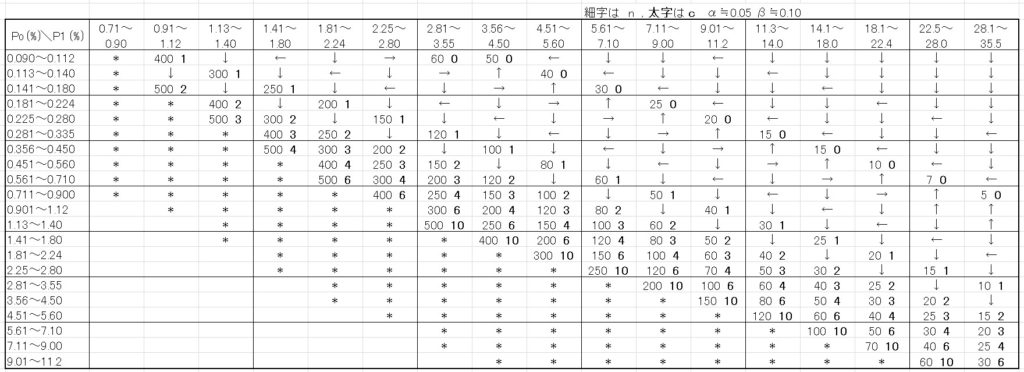
部分的に拡大します↓
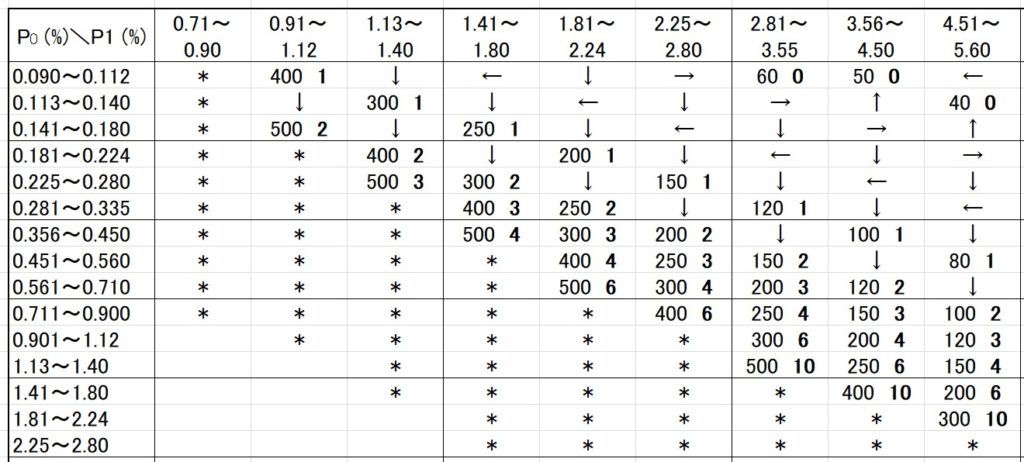
さて、この表を見ると、\(P_0 \) と\( P_1\) という確率があります。
\(P_0\) は売り手に対する(なるべく合格とさせたい)不適合品率の上限を、\(P_1\) は買い手に対する(なるべく不合格としたい)不適合品率の下限を表します。
なお、生産者のリスク\(α\)%(本来は合格のロットを不合格にする)と、消費者のリスク\(β\)%(本来は不合格のロットを合格にする)は、一般的には\(α=0.05\)%、\(β=0.10\)%と設定します。
この記事で使用している「JISZ 9002 計数基準型1回抜き取り検査表」も、\(α=0.05\)%、\(β=0.10\)%としたものを使用しています。
では実際に表の読み取りをしてみましょう!
\[\]
例1)\(P_0=0.8, P_1=3.0\) の時
該当する数値は、計数基準型1回抜き取り検査表より、「250 4」 となります。(下図)
\(P_0, P_1\) がどの範囲に入るかで判断します。
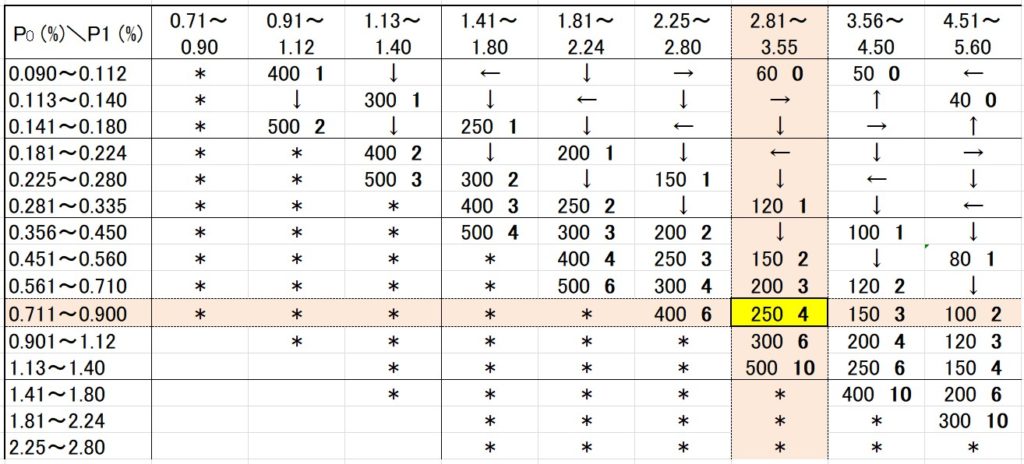
「250 4」が意味するところは、サンプル数\(n=250\) 個で、合格判定個数\(c=4\) 個となります。
つまり、サンプル数\(n=250\)個中、不適合品が \(5\) 個以上出た場合、そのロットは不合格となります。
\[\]
例2)\(P_0=0.4, P_1=3.0\) の時
該当する数値は、計数基準型1回抜き取り検査表より・・・「↓」!
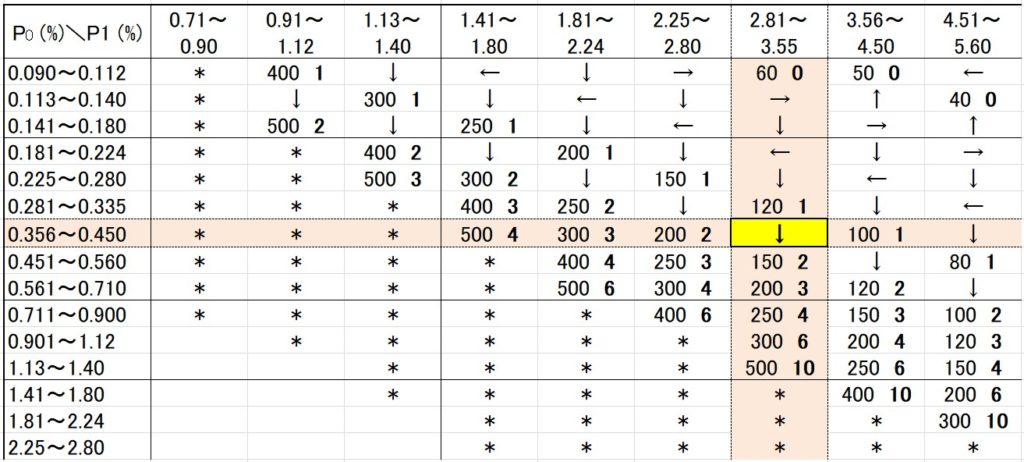
なんと数値ではありません!
しかし焦らないでください。これは下(↓)の数値を使用しろ、という意味です。
つまり、下の数値である「150 2」が該当する数値になります。
サンプル数\(n=150\) 個に対して、合格判定個数\(c=2\) 個となります。
\[\]
矢印は数値に当たるまで、その方向に進んでいきます。
例えば、\(P_0=0.25, P_1=5.0\)の場合は、「↓←↓」とたどっていき、「100 1」 が該当する数値となります。
\[\]
例3)\(P_0=2.0, P_1=5.0\) の時
さて、この時の該当する数値は、表より・・・
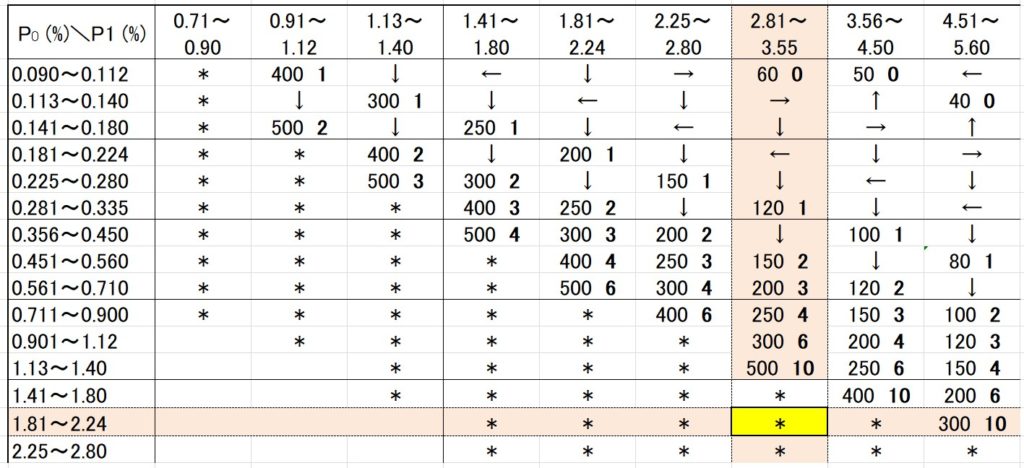
なんと「*」!!!
これはもうわけが分かりませんよね。
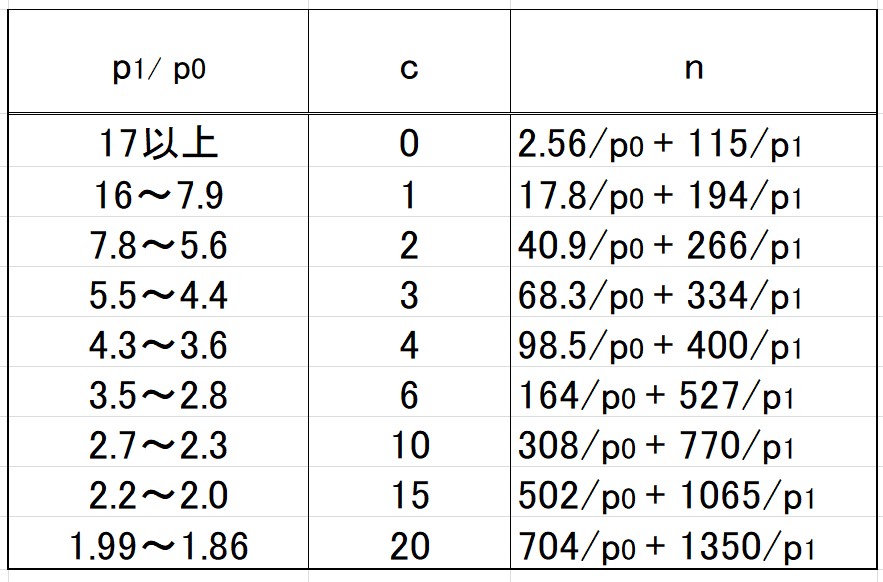
もしも「*」に遭遇してしまった場合は、「抜き取り検査補助表」を使用します。(下表)
\[\]
「抜き取り検査補助表」では、まず左端の\(p_1/p_0\) を計算します。
今回の場合ですと、\(5.0/2.0=2.5\) となります。
\(2.5\) ということは、「\(2.7~2.3\)」の間に入ります。
\[\]
そのまま右に読むと、\(c=10,n=308/p0 + 770/p1\) と書かれています。
よって、合格判定個数\(c=10\) となります。
\[\]
サンプル数\(n\) は、\(n=308/p0 + 770/p1\) を計算して、\(n=367\) となります。
※もしサンプル数\(n\) が計算で割り切れずに、小数点以下が発生した場合は、切り上げをします。
例)\(n=598.27\) ⇒サンプル数は\(599\) 個
\[\]
これで、計数基準型抜き取り検査の説明は終了です。
\[\]
⑤計量基準型抜き取り検査
計量基準型抜き取り検査も、計数基準型抜き取り検査と同様に、\(p_0,p_1\) を使って、「試料の大きさ\(n\) と合格判定値を計算するための係数\(k\) 」を求めます。
(。´・ω・)?アレ?
・・・先ほどとは呼び方が変わりました。
計量基準型抜き取り検査では、「JISZ 9003」記載の「付表2\(p_0\) (%),\(p_1\)(%)をもとにしての試料の大きさ\(n\) と合格判定値を計算するための係数\(k\) を求める表」 を使用します。
・・・名前が長い・・・
:(´ཀ`」 ∠):
例えば、\(P_0=1.0,P_1=5.0\) の時は、\(n=18,k=1.94\) となります。

一部拡大↓

\[\]
さて、問題はここからです。
計量基準型抜き取り検査では、抽出したサンプルから平均値を求め、その平均値が
- (1)上限合格判定値以下であればロット合格
- (2)下限合格判定値以上であればロット合格
の二種類があります。
\[\]
(1)上限合格判定値の求め方
\[上限合格判定値=上限規格値-k×ロットの標準偏差\]
(2)下限合格判定値の求め方
\[下限合格判定値=下限規格値+k×ロットの標準偏差\]
符号が反転しているだけで、規格値よりも中心側に合格判定値が来るように設定します。
\[\]
では例題を考えてみましょう。
例)金属板Aは厚み10.0mm以上が規格されている。\(p_0=1.0,p_1=5.0\) の時の下限合格判定値を求めよ。
ただし、ロットの標準偏差は0.5mmとする。
\[\]
早速解いてみます。
厚みは厚いほうが良いとされているので、下限合格判定値を求めます。
すると、「付表2\(p_0\) (%),\(p_1\)(%)をもとにしての試料の大きさ\(n\) と合格判定値を計算するための係数\(k\) を求める表」より、
\(p_0=1.0,p_1=5.0\) のとき、\(n=18,k=1.94\) となります。
よって、下限合格判定値は、
\[下限合格判定値=10.0+1.94×0.5=10.97\]
よって、サンプル数\(n=18\) 個の平均が10.97以上となれば、ロット合格となります。
なお、計量基準型抜き取り検査は、QC検定2級にほぼ出題されません!

\[\]
ポイントとして、計量基準型抜き取り検査は、計数基準型抜き取り検査よりも少ないサンプル数でロットの合否判断が可能 ということだけ覚えておきましょう。
※計数基準型抜き取り検査では、\(p_0=1.0,p_1=5.0\)のときは、サンプル数\(n=120\)、合格判定個数\(c=3\) となります。
\[\]
まとめ
①検査の種類は、「受入検査、中間検査、最終検査」
②検査の方法は、「全数検査、間接検査、抜き取り検査」
③OC曲線は、ある不適合品率のロットが合格する確率を表した曲線
④計数基準型抜き取り検査では、専用の表を読み取る
⑤計量基準型抜き取り検査はほぼ出題されない!?
\[\]
今回は検査について学びました。
次回からは管理図について学んでいきましょう!














[…] 次回は検査について勉強していきます。 […]
[…] OC曲線の詳細は、記事「検査の種類と方法」をご参照ください。 […]
突然のコメント失礼いたします。
とても丁寧に書かれていたので、非常に分かりやすかったです。
1点気になったのですが、p0、p1は生産者危険と消費者危険の確率ではなく、不適合品率の上限と下限ではないでしょうか・・・?
こちらの勘違いであれば、大変申し訳ございません。
ご指摘ありがとうございます。
おっしゃる通りです。
P0は売り手に対する不適合品率の上限を、P1 は買い手に対する不適合品率の下限を表します。
記事の内容を更新しましたので、引き続き当ブログをご贔屓いただければ幸いです。