平均値に関する検定2 :t分布 t検定

公開日2020年5月5日 最終更新日 2022年7月31日
みなさんこんにちは、michiです。
前回は、「平均値に関する検定1」と称して母分散が既知の場合の検定について学びました。
今回は母分散が未知の場合のt検定について勉強してましょう。
キーワード「t検定」「t表」「自由度」
目次
①t分布を使った検定
母集団から標本を抽出し、その平均値を評価するには二つの統計量がありました。
使い分け方は
- 統計量\(Z\) は、正規分布から得られる統計量で、母分散が 既知
- 統計量\(t\) は、\(t\) 分布から得られる統計量で、母分散が 未知
今回は母分散が未知の場合の\(t\)分布から統計量を計算する方法について勉強していきます。

\[\]
②\(t\)表のミカタ
前回の「平均値に関する検定1」と同様に直接例題を解いて学んでいきたいのですが、その前に\(t\)表の使い方を理解する必要があります。
\(t\)表は下のような表です。
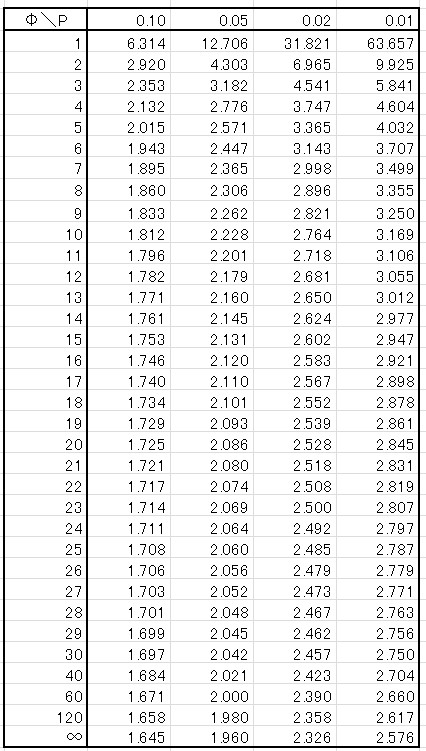
※自由度⇒∞ で正規分布表の「PからKpを求める表」と同じになります。
((((;´・ω・`)))ガクガク
正規分布表と比較すると、自由度\(Φ\)があります。
\(t\)分布は、「左右対称で自由度によって形が変わる」分布のためです。

分布の形が変わるということは、採択域と棄却域の境界となる棄却限界値が、自由度によって変わることを意味します。
ですので、\(t\)検定では自由度(サンプル数\(-1\))が重要になります。
\[\]
もう一つポイントがあります。
それは、\(t\)表に書かれている確率Pは両側棄却域の合計確率というとです。
図で表すと下のようになります。
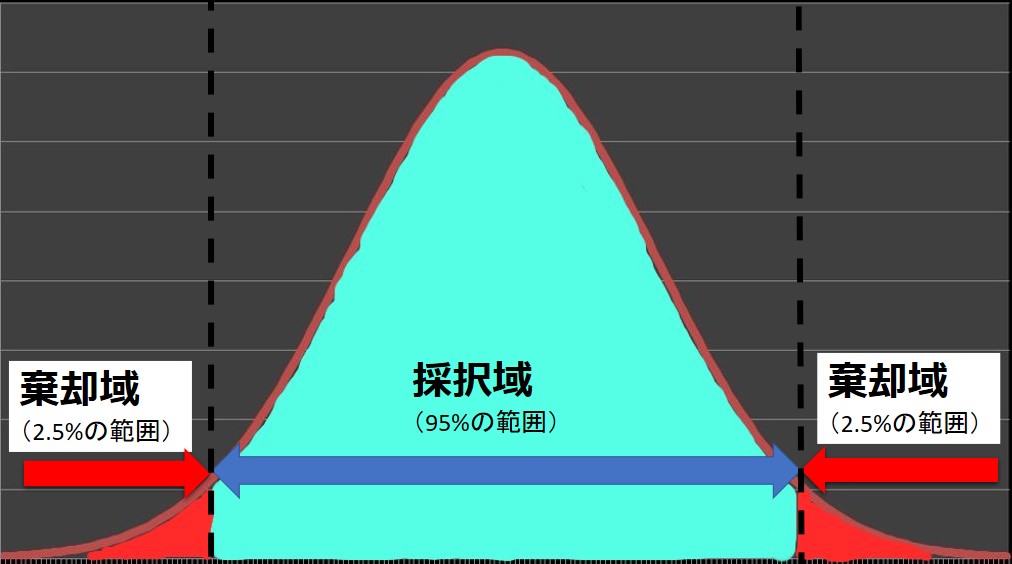
※\(t\)表の確率 P=0.05 の場合
よって、両側検定の場合、第一種の誤りが5%であれば、P=0.05の列を見ればOKです。
正規分布表では、第一種の誤りが5%の場合は、P=0.025をみました。
正規分布表「PからKpを求める表」との相違点なので気を付けましょう!
\[\]
③両側検定の\(t\)分布
\(t\)表のミカタもわかりましたので、例題を解いてみましょう。
問)母平均 \(μ=20.0\)の母集団から、\(n=9\)個のサンプルを抽出しました。サンプルの標本平均を調べると、\(\bar{x}=21.4\)で、不偏分散は\(V=4.0\) でした。
この時、母平均に対し標本平均は変化したか?第一種の誤りを5%として答えてね。
\[\]
今回も問題と解く前に、問われているものは何かを、以下の三つのキーワードをチェックします。
- 平均の変化か、ばらつき(分散)の変化か
- 変化の有無か、大小関係か
- 母分散が既知か、不偏分散のみが既知か
今回の問題は「平均の変化、変化の有無、不偏分散のみが既知」ですので、\(t\)分布の統計量\(t\)を使います。
\[\]
すると、
今回の帰無仮説は「母平均に対し、標本平均の変化がない:\(μ=\bar{x}\)」で、対立仮説は「母平均に対し、標本平均の変化がある:\(μ≠\bar{x}\)」 です。
統計量\(t\)は、正規分布の統計量\(Z\)の 母分散⇒不偏分散 なので
\[t\qquad =\frac{\bar{x}-μ}{\sqrt{\frac{V}{n}}} \qquad=\frac{標本平均-母平均}{\sqrt{\frac{不偏分散}{サンプル数}}}\]
今回の問題の数値をあてはめると
\[t\qquad =\frac{\bar{x}-μ}{\sqrt{\frac{V}{n}}} \]
\[\qquad=\frac{21.4-20}{\sqrt{\frac{4}{9}}}\]
\[=\frac{1.4}{\frac{2}{3}}\qquad\]
\[= 2.1\]
\[\]
次に\(t\)表から棄却限界値を見積もるのですが、今回の問題は変化の有無を問われています。
有意水準(第一種の誤り)\(α\)=5% として時の自由度8(サンプル数 – 1)の値は・・・
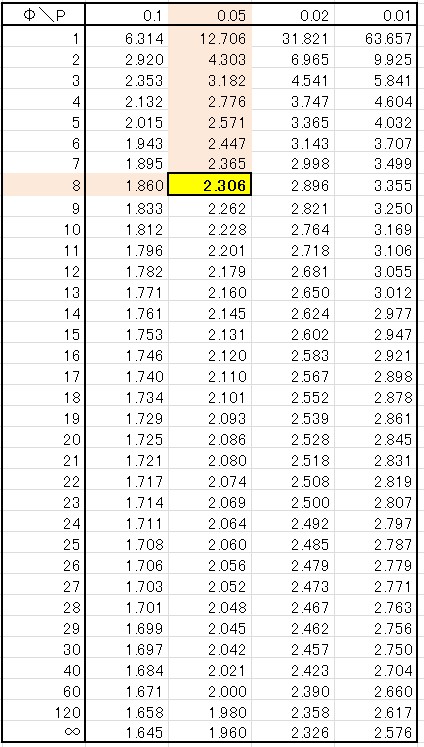
2.306 です。
この時\(t\)分布では、「棄却限界値\(t\)(8:0.05)=2.306」と書きます。
「棄却限界値\(t\)(自由度:有意水準(第一種の誤り))=○○○」と表現されます。
\[\]
すると、棄却限界値\(t\)(8:0.05)=2.306 > 統計量\(t\)= 2.1 ですので、統計量\(t\)は採択域内にあると判断します。
よって、帰無仮説「母平均に対し、標本平均の変化がない:\(μ=\bar{x}\)」が採択され、「平均値に変化があるとは言えない」となります。
\[\]
④片側検定の\(t\)分布
さて、今度は片側検定で考えてみます。
問)母平均 \(μ=20.0\)の母集団から、\(n=9\)個のサンプルを抽出しました。サンプルの標本平均を調べると、\(\bar{x}=21.4\)で、不偏分散は\(V=4.0\) だった。
この時母平均に対し標本平均は大きくなったか?第一種の誤りを5%として答えてね。
\[\]
今回の問題は「平均の変化、大小関係、不偏分散のみが既知」ですので、\(t\)分布の統計量\(t\)を使います。
今回の帰無仮説は「母平均に対し、標本平均の変化がない:\(μ=\bar{x}\)」で、対立仮説は「母平均に対し、標本平均は大きくなった:\(μ<\bar{x}\)」 です。
さて、先ほどと同様に統計量\(t\)を計算すると、
\[t\qquad =\frac{\bar{x}-μ}{\sqrt{\frac{V}{n}}} \]
\[=2.1\]
\[\]
今回は片側検定ですので、棄却限界値が両側検定の時と変わります。
結論からいうと、「棄却限界値\(t\)(8:0.1)=1.860」 です。
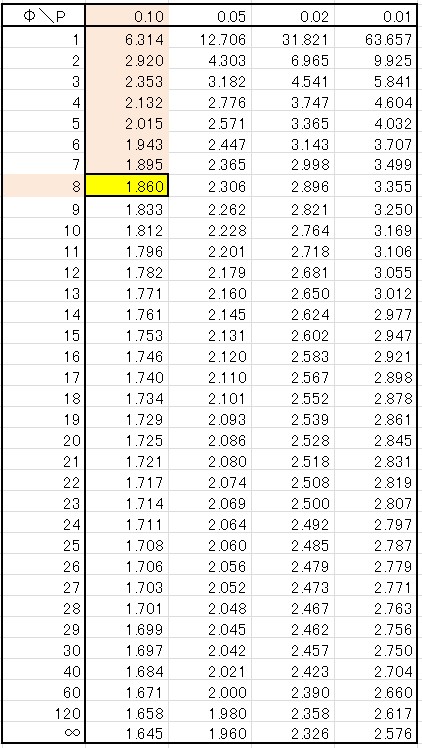
すると、棄却限界値\(t\)(8:0.1)=1.860 < 統計量\(t\)=2.1 ですので、統計量\(t\) は棄却域内にあると判断します。
よって、帰無仮説「母平均に対し、標本平均の変化がない:\(μ=\bar{x}\)」が棄却され、対立仮説である「母平均に対し、標本平均は大きくなった」が採択されます。
問題に対する回答は、「平均値は大きくなった」 です。
\[\]
⑤\(t\)分布の片側検定で\(α\)を2倍にする理由
片側検定の答えをみると次の疑問が生まれます。
棄却限界値を決めるときの確率 P=0.1 なら、第一種の誤りは10%になるのでは?
(。´・ω・)?
\[\]
はい、そうです。
ただしそれは両側検定の場合です。

\(t\)表では、「確率Pは両側棄却域の合計確率」なので、あわせて10%の棄却限界値が、片側検定5%の棄却限界値となります。
そのため、もう一方の棄却域(今回は小さい側)を無視することで、片側検定5%の棄却域が設定できます。

\[\]
⑥正規分布表と\(t\)表の混乱防止
正規分布表と\(t\)表の表現方法は混乱してしまいそうです。
●正規分布表の両側検定では、第一種の誤りの確率Pが半分の時の確率変数が棄却限界値となる。
●\(t\)表の片側検定では、第一種の誤りの確率Pが倍の時の確率変数が棄却限界値になる。
(゚ω。)アリャ?
紛らわしいですよね。混乱しそうです。
\[\]
しかしご安心を。QC検定では付表が問題用紙のどこかにあります。
そしてその付表には下の図が通常ついています。
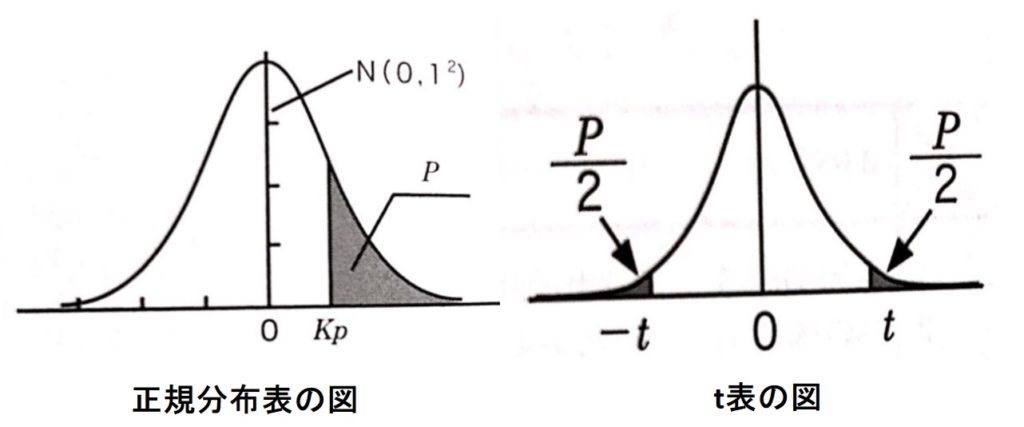
この図をみれば、第一種の誤りに対し、「確率Pを半分にするのか、倍にするのか、そのまま読み取っていいのか」が分かります。
重要なことは、「正規分布か\(t\)分布か」と「両側検定か片側検定か」です。
\[\]
まとめ
①母分散の値が未知で、平均の変化を知りたい場合は\(t\)分布で考える
②両側検定で\(t\)表を使う場合は、確率Pをそのまま読み取る
③片側検定で\(t\)表を使う場合は、確率Pを倍にする
④正規分布表とt表では確率の表記方法が違うので注意
⑤ QC試験本番では、付表についているであろう図で確認
\[\]
今回は\(t\)表を使った\(t\)検定について学びました。
次回は、\(χ^2\)カイ二乗検定について勉強しましょう。















[…] 次回からは、正規分布、t分布、(χ^2)カイ二乗分布、F分布のそれぞれの分布に対しての検定方法について、勉強していきましょう。 […]