工程能力指数の使い方

公開日2020年3月8日 　最終更新日 2022年5月6日

みなさんこんにちは、michiです。

前回の記事で正規分布表の見方について勉強しました。

今回は工程管理の手法一つ、工程能力指数について学んでいきます。

キーワード　「工程能力指数」「Cp」「Cpk」

①工程能力指数とはなにか

Wikipediaによると、「工程能力指数とは、品質管理の分野において、ある工程の持つ工程能力を定量的に評価する指標の一つである。工程能力は工程が管理状態で、かつ、安定した状態で予測可能な場合のみ評価できる」　とあります。

(;´･ω･)

・・・ひとことでいうと、「工程を管理するための指標」です。

工程能力指数は、「Process Capability Index」　と英語で言います。そこから頭文字をとって「Cp」と表現されます。

\[\]

②両側規格の工程能力指数

両側規格の工程能力指数は以下の式であらわされます。

\[工程能力指数(Cp) = \frac{上限規格 – 下限規格}{6 × 標準偏差(σ)}\]

イメージ図は下です。

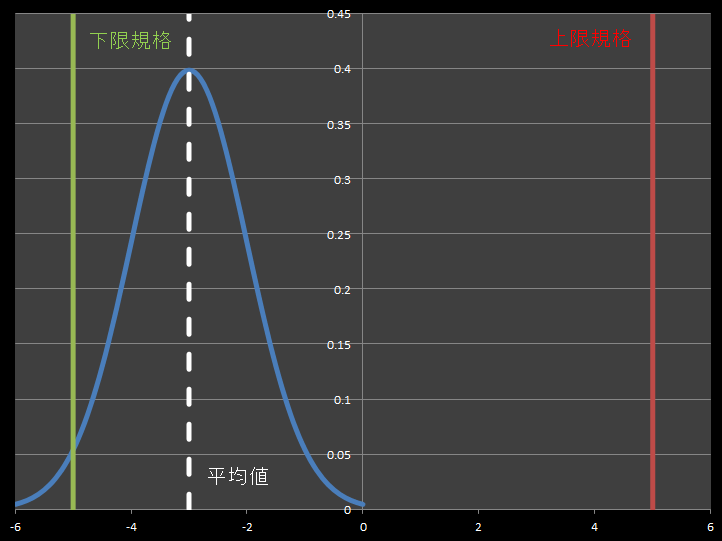
※グラフは±3の範囲のみ表示していますが、実際の分布は±∞まであります。

測定データから得られた標準偏差、製品規格の上限と下限の3つから成ります。

ここで注目すべきは、標準偏差のみが測定データで使用されている点です。

両側規格の工程能力指数では、「上限規格－下限規格」という「製品規格の幅」と、標準偏差という「製品のばらつきの幅」の比を評価しています。

\[\]

両側規格の工程能力指数は、「製品規格」という箱に対し、製品の大きさがどのくらい余裕をもっているか、あるいはどのくらいはみ出るかをあらわしています。

「規格の幅」と「標準偏差（製品のばらつきの幅）」の二つの幅で評価するのが「両側規格」です。

\[\]

③片側規格の工程能力指数

片側規格の工程能力指数は以下の式であらわされます。

\[片側工程能力指数(Cpk) = \frac{上限規格 – 平均値}{3 × 標準偏差(σ)}\]

または、

\[片側工程能力指数(Cpk) = \frac{平均値 -下限規格 }{3 × 標準偏差(σ)}\]

両側規格と比較して異なる点を考えてみましょう。

• 工程能力指数の名前が「Cpk」になっている
• 平均値が使われている
• 分母の標準偏差の前の数字が3　になっている

\[\]

Cpkは、両側規格のCpにｋが追加されています。

これは、「Process Capability Index　Katayori」 の頭文字をとっています。

「Katayori」は「偏り」のことで日本語です。

Σ(･ω･ﾉ)ﾉ！

このように、「規格値と平均値の差」と「標準偏差（製品のばらつきの幅）」の二つで評価するのが「片側規格」です。

\[\]

④なぜ片側規格を考えるのか

すでに両側規格があるのに、なぜ片側規格が必要なのでしょうか？

それは、「両側規格では、ずれを評価できない」からです。

もう一度両側規格の式を見てみましょう

\[工程能力指数(Cp) = \frac{上限規格 – 下限規格}{6 × 標準偏差(σ)}\]

この式では「規格の幅」と「標準偏差（製品のばらつきの幅）」のみで評価していました。

幅の評価では余裕があっても、その分布が規格値に近い場合、実際には余裕があるとは言えません。

(。´･ω･)?

\[\]

次のグラフを見てみましょう！

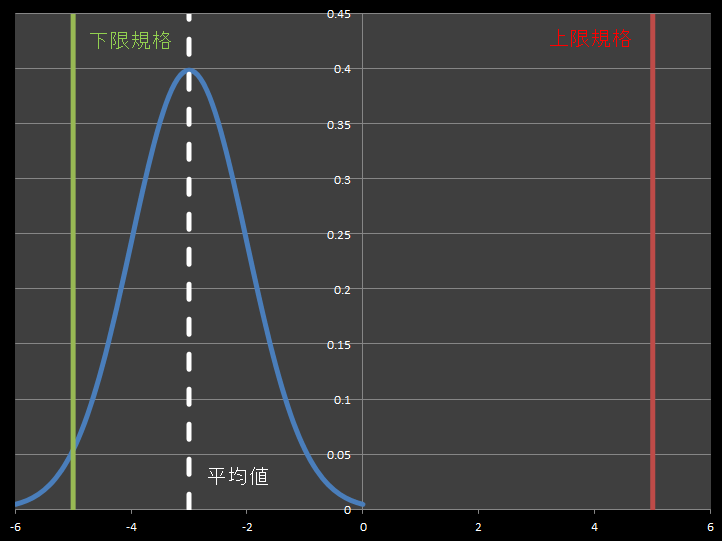
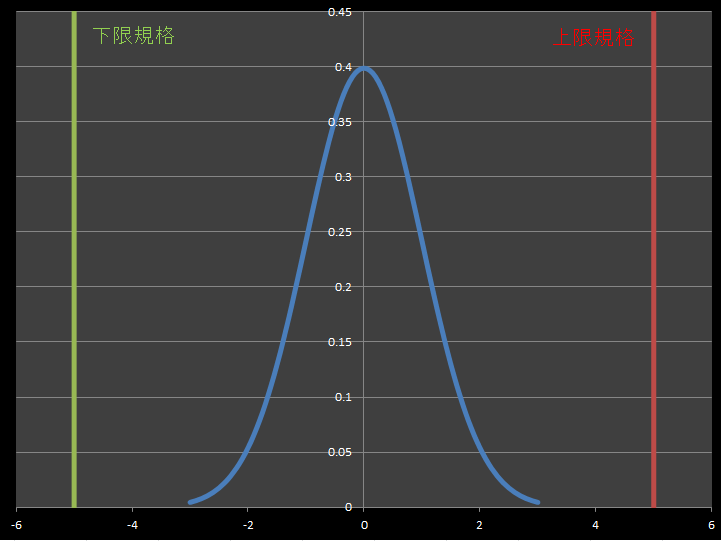
※グラフは-6から0の範囲のみ表示していますが、実際の分布は±∞まであります。

グラフ2 はグラフ１ と同じ「標準偏差」「上限規格」「下限規格」です。

しかし、平均値（グラフの中心）には偏りがあります。

\[\]

平均値に偏りがあるため、分布の一部が下限規格を下回っています。

下限規格を下回っている状態は望ましい状態とはいえません。

(◎´･ω･)´-ω-)ｳﾝ

そこで片側規格を使用し、「標準偏差（製品のばらつきの幅）」と「平均値」から、「規格値」に対してどれだけ裕度があるかを指標としていきます。

\[\]

⑤工程能力指数の判断基準

工程能力指数を計算したら、以下の表で評価します。

Cp,Cpk≧1.67	十分すぎる
1.67＞Cp,Cpk≧1.33	十分満足している
1.33＞Cp,Cpk≧1.0	まずまずである。十分な状態に改善する
1.0＞Cp,Cpk≧0.67	不足しているので、1.33になるように改善処置をとる
0.67＞Cp,Cpk	非常に不足している。原因を究明し、是正処置をとる

\[\]

グラフ1の両側規格Cpは、「1.67」

グラフ2の上限規格に対する片側規格は「2.66」、下限規格に対する片側規格は「0.67」　です。（少数第3位を四捨五入）

\[\]

この計算結果から、グラフ1の工程は十分管理されているといえます。

しかし、グラフ2については、上限規格に対しては十分管理されているといえますが、下限規格に対しては不足しているため、改善処置が必要　となります。

※片側規格を評価する場合は、「上限規格」と「下側規格」のCpkを計算したのち、Cpkの小さい値を採用します。

両側規格Cpのみでは判断できないずれを片側規格Cpkを考慮することによって、本当の工程管理能力を評価できるようになります。

\[\]

⑥なぜ標準偏差を6倍、3倍するのか

さて、一通り工程能力指数が何かを学びましたが、疑問があります。

なぜ、分母の標準偏差を6倍または3倍するのでしょうか？

(。´･ω･)?

この答えのヒントは、記事「不偏分散ではだめ？なぜ標準偏差」にまとめました。

ポイントは、中心から標準偏差分だけ離れた点が変曲点になることです。

では、この標準偏差\(σ\)を3倍するとどうなるか、見てみましょう！

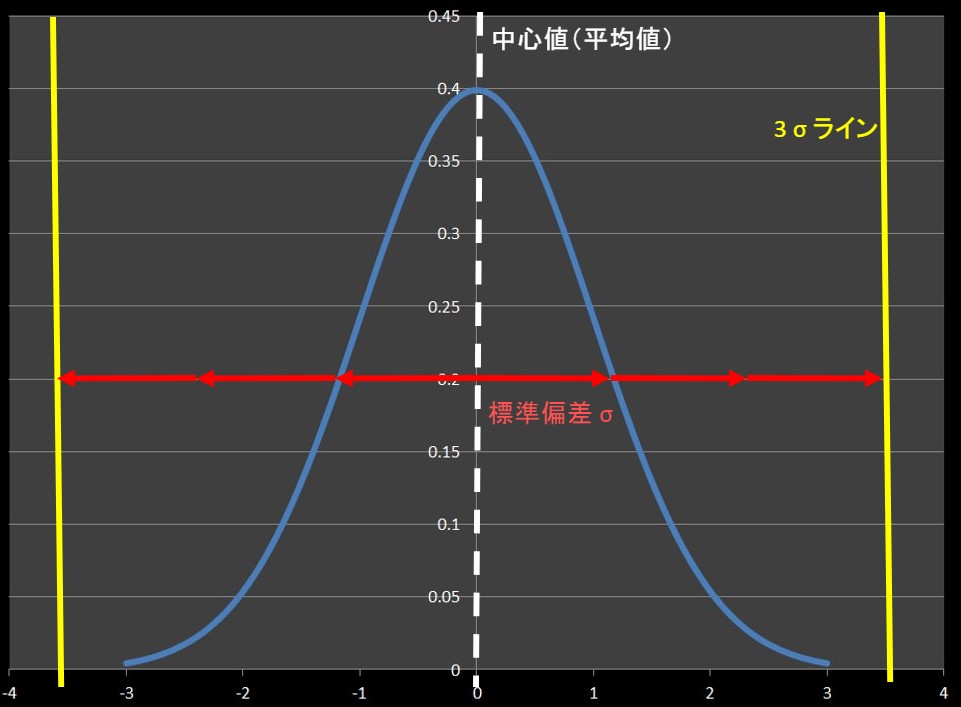
※グラフは±3の範囲のみ表示していますが、実際の分布は±∞まであります。

黄色の直線が正規分の中心値から、左右それぞれ3\(σ\)離れた位置にあります。

この黄色の直線の内側に測定値が分布する確率は　99.7%　になります。

99.7%という数値は統計的な計算から求められます。

重要なことは、黄色の直線の外側には0.3%しか存在確率がないということです。

つまり、黄色の直線外側に測定値が存在することは、滅多にないこと（＝異常？）と考えられます。

\[\]

さて、工程能力指数Cp　の計算式を思い出してみましょう。

\[工程能力指数(Cp) = \frac{上限規格 – 下限規格}{6 × 標準偏差(σ)}\]

\[\]

改めて式をみると、「規格の幅　と　測定値の99.7%が存在する領域　の比」を計算していることが分かります。

Cp=1.0とは、規格の幅と測定値の99.7%が存在する領域が同じことを意味します。

Cp=1.0から、\(σ\)分の幅の大小で工程能力指数の評価が変わります。

\[\]

では、片側規格の工程能力指数はどうなのか見てみます、計算式は下式の通りです。

\[片側工程能力指数(Cpk) = \frac{上限規格 – 平均値}{3 × 標準偏差(σ)}\]

または、

\[片側工程能力指数(Cpk) = \frac{平均値 -下限規格}{3 × 標準偏差(σ)}\]

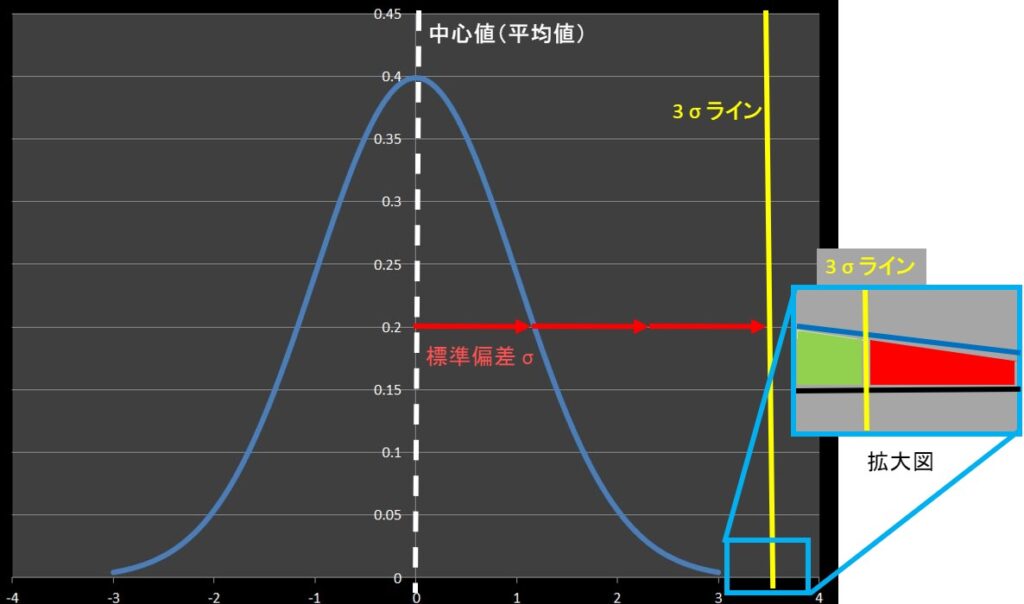
今回は片側規格の右側だけを例として考えます。

両側規格では規格の幅と99.7%の存在領域の比をみましたが、片側規格では、99.7%の境界値と規格値を比較します。

※拡大図の緑色の領域は99.7%の存在領域、赤色の領域は0.3%の存在領域

\[\]

もし、99.7%の境界値と規格値が同じ値であれば、それはCpk=1.0を意味します。

Cpkでは6倍ではなく3倍で求める理由は、平均値から3\(σ\)離れた位置が99.7%の境界値となるからです。

\[\]

まとめ

①工程能力指数とは、「程を管理するための指標」

②両側規格Cpは規格の幅に対するばらつきの幅で評価

\[工程能力指数(Cp) = \frac{上限規格 – 下限規格}{6 × 標準偏差(σ)}\]

③片側規格Cpkの計算式は、

\[片側工程能力指数(Cpk) = \frac{上限規格 – 平均値}{3 × 標準偏差(σ)}\]

または、

\[片側工程能力指数(Cpk) = \frac{平均値 -下限規格 }{3 × 標準偏差(σ)}\]

④片側規格Cpkは、両側規格Cpにくらべ規格値に対する平均値も考慮

⑤工程能力指数は両側規格Cpか片側規格Cpkで考え、1.33以上になるように改善する

⑥標準偏差\(σ\)を6倍または3倍する理由は、規格値と99.7%の存在領域の比を計算しているから

\[\]

次回は二項分布の考え方について説明していきます。

⇒オススメ書籍はこちら

⇒サイトマップ