QC検定3級 プチ問題 No.29 総合問題1 ※計算
公開日2021年1月12日 最終更新日 2021年9月12日
みなさんこんにちは、michi です。
それでは早速3級の問題を解いてみましょう!
今回のテーマは、 総合問題 です。
問)次の問題文を読んで、標準偏差 \(σ\) を求めましょう。
製品Aの規格値は上限が18、下限が10である。
製品Aの片側規格の工程能力指数Cpk は0.5で、この時の製造工程における管理図は以下の通りです。

なお、\(\bar{x}-R\) 管理図用係数表は以下の通りである。

注) \(\bar{x}\) 管理図と\(R\)管理図のグラフが同じで手抜き! とかは思わないこと!
\[\]
答え・解説は↓
解答
※ドラッグで表示
\(σ\)= 2
\[\]
解説)
今回の問題は管理図の見方と工程能力指数の計算方法の両方を問われている、複合問題になります。
少し難しいですが、しっかりと復習しておきましょう。
\[\]
標準偏差 \(σ\) は、工程能力指数から計算できます。
今回の問題では、工程能力指数Cpkが 0.5 であると書かれています。
しかも、片側規格の工程能力指数であることが、わかっているため、以下の式のいずれかで計算できます。
\[片側工程能力指数(Cpk) = \frac{上限規格 – 平均値}{3 × 標準偏差(σ)}\]
\[片側工程能力指数(Cpk) = \frac{平均値 -下限規格 }{3 × 標準偏差(σ)}\]
\[\]
片側規格の場合は、数値の小さいほうを採用する約束でした。
つまり、規格値と平均値の差が小さいほうを採用します。
問題文より、上限規格は 18 、下限規格は 10 ですから・・・
(。´・ω・)? 平均値わからん・・・
\[\]
そう、平均値が分かりません!
しかし、管理図があるので、管理図から平均値を求めましょう。
今求めようとしている平均値は \(\bar{x}\) 管理図の中心線(CL=\(\bar{\bar{x}}\)) に該当します。
\(\bar{x}\) 管理図の中心線は・・・
\[\]
(# ゚Д゚) 書いてない!
なんと、普通はありえませんが、管理図の中心線(CL)が書かれていません。
しかし、上方管理限界線は書かれています。
\(\bar{x}\) 管理図における管理限界線は以下の式で表されます。
- 上方管理限界線 \(UCL = \bar{\bar{x}} +A_2×\bar{R} \)
- 下方管理限界線 \(LCL = \bar{\bar{x}} -A_2×\bar{R} \)
\[\]
上方管理限界線は問題文より 25.2 であることが、わかっています。
また、\(\bar{x}\) 管理図には、「\(n=3\)」 と書かれています。
\(n=3\) とは群の大きさ(サンプルサイズ)のことを表します。
\(\bar{x}-R\) 管理図用係数表より、\(n=3\) の時の係数 \(A_2\) は1.02 であることが分かります。
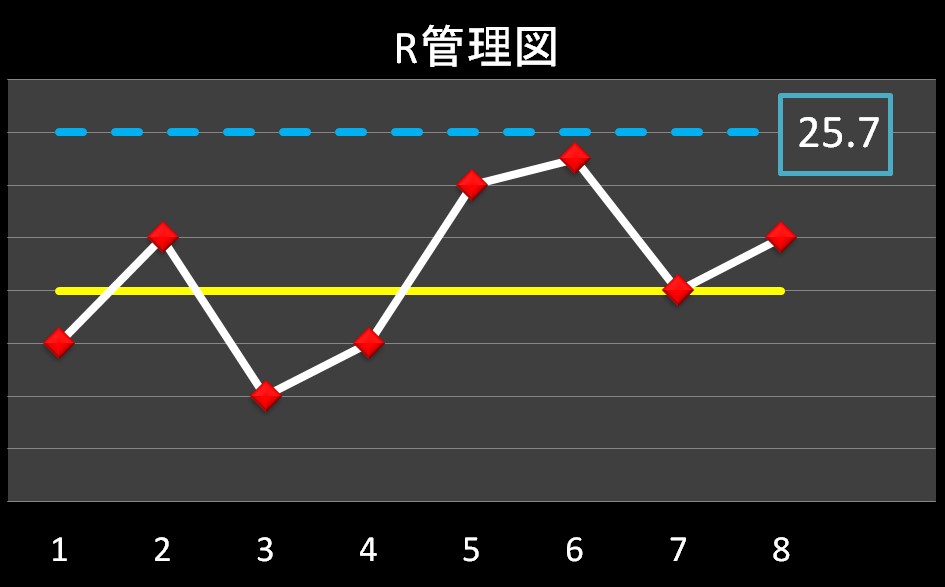
あとは \(\bar{R}\) がわかればよいので、\(R\) 管理図の中心線(=\(\bar{R}\)) を見ると・・・
\[\]
(б´д`;)ダカラサ-…。
なんということでしょう!
\(R\) 管理図の中心線(=\(\bar{R}\)) が書かれていません!
しかし、上方管理限界線はあります。
\(R\) 管理図における管理限界線は以下の式で表されます。
- 上方管理限界線 \(UCL = D_4 × \bar{R}\)
- 下方管理限界線 \(LCL = D_3 × \bar{R}\)
※今回はサンプルサイズが 6 以下なので、下方管理限界線はありません。
\(R\) 管理図の上方管理限界線は、図より 25.7 です。
また、\(\bar{x}-R\) 管理図用係数表より、\(n=3\) の時の係数 \(D_4\) は2.57 であることが分かります。
やっと準備が整ったので、順番に計算していきます。
\[\]
①\(\bar{R}\) を求める。
\(R\) 管理図より、UCL=25.7 なので
上方管理限界線 \(UCL = D_4 × \bar{R}\) より
\[25.7=2.57× \bar{R}\]
\[\bar{R}=10\]
\[\]
②\(\bar{x}\) を求める
\(\bar{x}\) 管理図より、UCL=25.2 なので
上方管理限界線 \(UCL = \bar{\bar{x}} +A_2×\bar{R} \)
\[25.2=\bar{\bar{x}}+1.02×10\]
\[\bar{\bar{x}}=25.2-10.2= 15\]
\[\]
③片側規格の工程能力指数 から標準偏差 \(σ\) を計算する
②までの計算で全体の平均値(\(\bar{\bar{x}}\)) を計算しました
片側規格の工程能力指数は、小さいほうを採用します。
それは言い換えると、規格と平均値の近いほうを採用することと同じでした。
さて、問題文より上限規格値は18、下限規格値は10であり、平均値が15ですので、上限規格値の工程能力指数を採用します。
すると、問題文より「片側工程能力指数(Cpk)=0.5」 ですので・・・
\[片側工程能力指数(Cpk) = \frac{上限規格 – 平均値}{3 × 標準偏差(σ)}\]
\[0.5=\frac{18-15}{3×σ}\]
\[3×σ=\frac{3}{0.5}\]
\[σ=\frac{6}{3}\]
\[σ=2\]
\[\]
今回の問題は長かったですね。
こんな問題は3級では出ないと思いますが、2級では出かねないのでしっかりと復習しておきましょう!
\[\]
今回の問題が解ければ、管理図と工程能力指数は一通り計算できる力量があります!
今回の説明は以下の記事をご参照ください。
\[\]











