ばらつきに関する検定2:F検定

公開日2020年5月7日 最終更新日 2022年6月19日
みなさんこんにちは、michiです。
前回は「分散に関する検定1」と称して\(χ^2\)カイ二乗検定について学びました。
今回は二つの集団の分散を比較する\(F\)検定について学んでいきます。
キーワード:「\(F\)検定」「\(F\)表」「不偏分散」
目次
①\(F\)表を使った検定
ばらつき(=分散)を評価するには二つの統計量がありました。統計量\(χ^2\)と統計量\(F\)です。両者の使い分け方は、
- 統計量\(χ^2\)カイ二乗は、母集団かの分散の変化を表す
- 統計\(F\)は、二つの母集団から得られた標本の分散の差異を表す
今回は二つの集団のばらつきを比較する、\(F\)検定を学びます。
\[\]
②\(F\)表のミカタ
いきなり問題を解く前に、今回も\(F\)表の見方から始めます。
\(F\)表は以下のような表です。
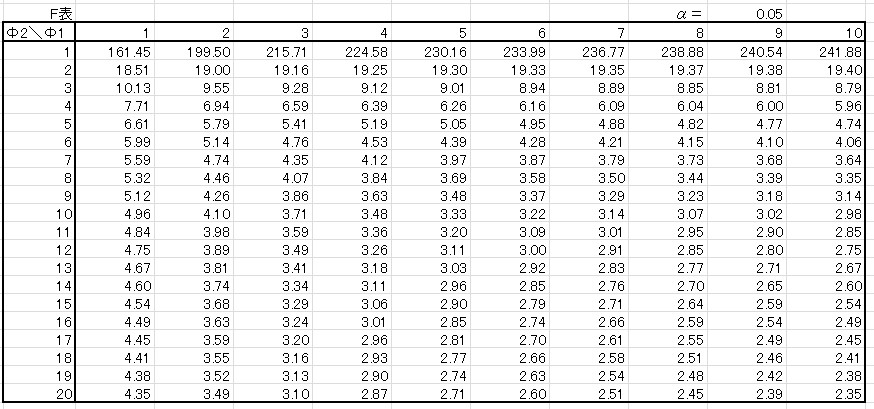
※もちろん自由度が10以上のものもあります。今回は抜粋です
\(χ^2\)カイ二乗表と似ている点と似ていない点がありますね。
- 似ている点:縦軸が自由度\(Φ_2\)
- 似ていない点:横軸も自由度\(Φ_1\)!
似ている点の理解ですが、\(F\)分布も\(χ^2\)カイ二乗分布も自由度で形の変わる分布関数です。

第一種の誤りが\(α\)%で固定されていても、\(F\)分布は自由度によって棄却域と採択域が変わります。
\[\]
次に似ていない点ですが、横軸も自由度になっています。
確かに二つの集団のばらつきを表したのが\(F\)分布ですので、二つの自由度があるのはわかります。
しかし、これでは第一種の誤りを\(α\)%としたときの確率がわかりません!
(。´・x・`。)ゥーンッ?? 困った
\[\]
表の右上をよく見ると・・・\(α\)=0.05 ・・・確率が書かれています。
そうなんです。\(χ^2\)分布では該当する確率Pの列から確率変数を求めていましたが、\(F\)表では該当する確率Pの表そのものから確率変数を求めます。
(○´・ω・`)b OK!
\[\]
さらに、\(F\)表には注意しなければいけない点がまだあります。
それは、「どちらの集団の自由度を縦軸or横軸にすればよいか」です。
もう一度\(F\)表を見てみましょう。
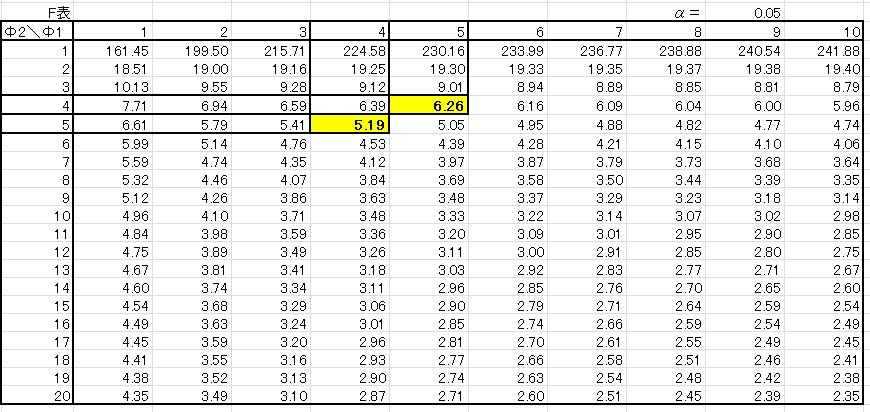
この表をみると、棄却限界値\(F\)(4,5:0.05)=5.19 ですが、棄却限界値\(F\)(5,4:0.05)=6.26 となっています。
※\(F\)検定では棄却限界値を、「棄却限界値\(F\)(自由度\(Φ_1\),自由度\(Φ_2\):第一種の誤り\(α\))」と表します。
このように、\(F\)表は縦軸と横軸の自由度を入れ替えると棄却限界値が変わってしまいます。
\[\]
③自由度の設定方法
自由度を適切に設定するにはどうすればよいでしょうか? 統計量\(F\)の定義を考えてみます。
\(F\)検定で使用される検定統計量\(F\)は以下の通りです。
\[F=\frac{不偏分散V_B}{不偏分散V_A}\]
この時、分子の不偏分散\(V_B\)の自由度を横軸の自由度\(Φ_1\)とし、分母の不偏分散\(V_A\)の自由度を縦軸の自由度\(Φ_2\) とします。
\[\]
では、不偏分散\(V_A\)と不偏分散\(V_B\)のどちらを分母or分子にすればよいのでしょうか?
ここで、検定統計量\(F\) を設定したときの条件が重要になります。
\[F>1\]
統計量\(F\)>1 が統計量\(F\)の条件です。この条件を満たすように分母と分子を設定し、分子が\(F\)表の横軸の自由度\(Φ_1\)となります。
\[\]
④両側検定の\(F\)分布
\(F\)表の見方もわかったので、早速問題を解いてみましょう。
問)装置Aで作られた製品aを 9個抽出し、平方和\(S_A\)を求めると 220 だった。装置Bで作られた製品bを 10個抽出し、平方和\(S_B\)を求めると 90 だった。
この時、装置Aと装置Bでは製品のばらつきに差はあるだろうか、第一種の誤りを5%として答えてね。
\[\]
いままでと同様に以下の三つのキーワードをチェックしましょう。
- 平均の変化か、ばらつき(分散)の変化か
- 変化の有無か、大小関係か
- 母分散が既知か、不偏分散のみ既知か
このキーワードを見ると「ばらつき(分散)の変化?、・・・変化の有無?、・・・?」という状況です。
いままでのやり方ではうまくいきません。しかし、比較対象は二つの集団ばらつき(分散)ですので、\(F\)検定を行います。
母分散はわかりませんが、平方和とサンプル数がわかるので、不偏分散を求めることは可能です。
\[\]
この時の帰無仮説は「二つの集団のばらつきに違いはない:\(σ_A^2=σ_B^2\)」で、対立仮説は「二つの集団のばらつきに違いがある:\(σ_A^2≠σ_B^2\)」です。
それでは、不偏分散を求めてから、統計量\(F\)を使って検定していきましょう。
装置Aで作られた製品aの不偏分散を\(V_A\)、装置Bで作られた製品bの不偏分散を\(V_B\)とすると、
\[V_A\qquad= \frac{平方和}{自由度(=サンプル数-1)}\qquad =\frac{220}{9-1}\]
\[=27.5\]
\[\]
\[V_B \qquad =\frac{90}{10-1} \qquad=10\]
次に\(F\) >1 となるように\(V_B\)を分母にすると、
\[統計量 F_0\qquad = \frac{V_A}{V_B} \qquad = \frac{27.5}{10} \qquad =2.75\]
となります。
この統計量\(F_0\)を\(F\)表から読み取った値と比較すると、不偏分散\(V_A\)が分子にあるので、自由度\(Φ_1\)は、製品aの自由度(=サンプル数-1) の8となります。
同様に、分母に不偏分散\(V_B\)がありますので、自由度\(Φ_2\)は製品bの自由度の9となります。
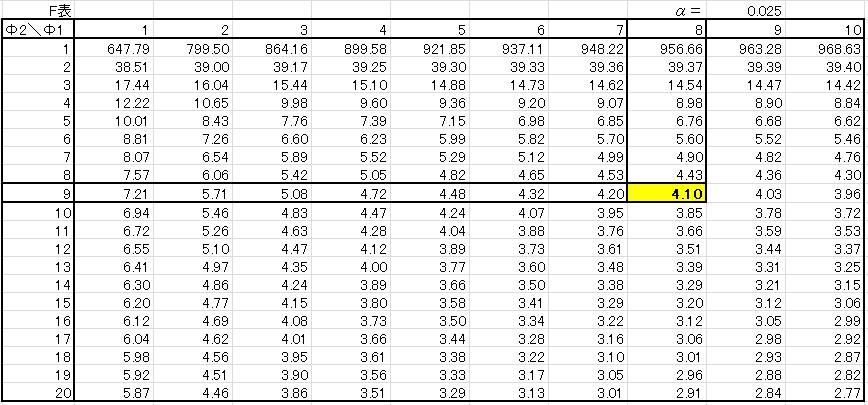
よって「棄却限界値\(F\)(8,9:0.025)=4.10」 となります。
今回は両側検定ですので、第一種の誤り\(α\)=5%に対し上側の棄却限界値を求める確率Pを P=0.025 として、\(F\)表をつかいました。
\(χ^2\)検定と同様に、下側の確率を求めるためP=97.5 の\(F\)表を使うと・・・
(。´・ω・)? そんなのなくない?
\[\]
そうなんです。\(F\)表は\(χ^2\)表のように95%以上の確率を表している表がありません。
しかも\(F\)分布は左右非対称なので、正規分布や\(t\)分布のようにプラス・マイナスの符号を変えるだけというわけにもいきません。
( ´・д・) どうしよう・・・
\[\]
そこで、以下の式変形を利用します。(定義より)
\[棄却限界値 F(Φ_2,Φ_1:0.975)=\frac{1}{棄却限界値 F(Φ_1,Φ_2:0.025)}\]
※この説明は次回の記事にまとめます。
すると、下側の棄却限界値は、
\[棄却限界値 F(Φ_2,Φ_1:0.975)=\frac{1}{4.10} =0.244\]
よって、棄却限界値と検定統計量\(F_0\)を比べると
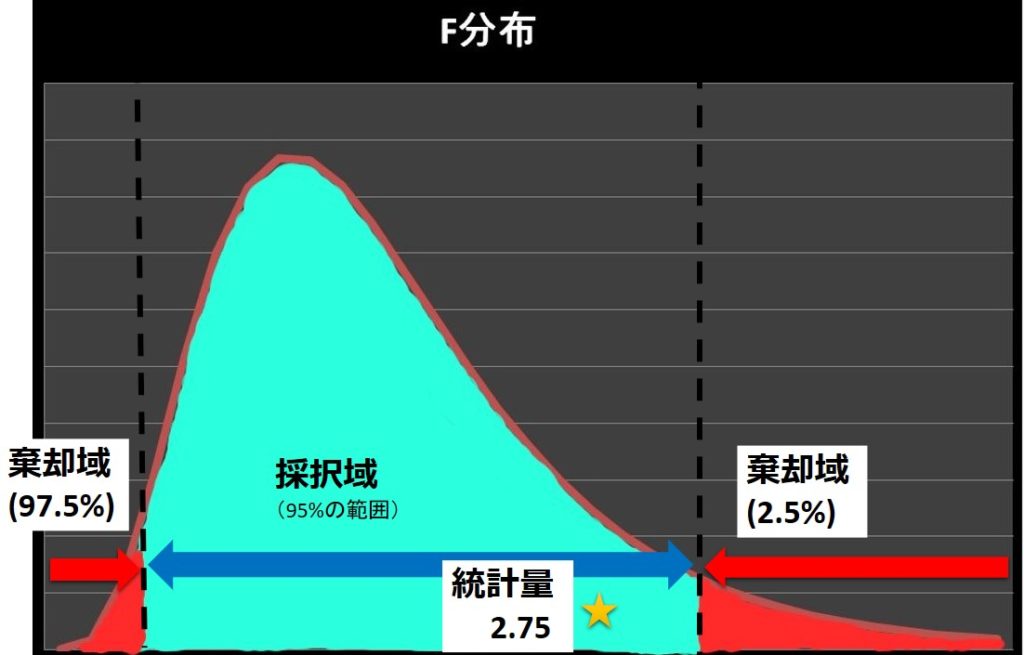
\[棄却限界値 F(Φ_2,Φ_1:0.975)=0.244 < 統計量 F_0 =2.75 \]
\[< 棄却限界値F(8,9:0.025)=4.10\]
統計量\(F\)は採択域内にあると判断されます。よって、帰無仮説の「二つの集団のばらつきに違いはない:\(σ_A^2=σ_B^2\)」が採択され、「ばらつきに違いがあるとは言えない」と判断します。
\[\]
⑤片側検定の\(F\)分布
次に、質問を一部変更し片側検定をしてみます。
問)装置Aで作られた製品aを 9個抽出し、平方和\(S_A\)を求めると 220 だった。装置Bで作られた製品bを 10個抽出し、平方和\(S_B\)を求めると 90 だった。
この時、装置Aは装置Bよりも製品のばらつきが大きいだろうか、第一種の誤りを5%として答えてね。
\[\]
先ほどの質問とパラメータは同じですが、問われている内容が変わりました。今回も三つのキーワードをチェックしてみます。
- 平均の変化か、ばらつき(分散)の変化か
- 変化の有無か、大小関係か
- 母分散が既知か、不偏分散のみ既知か
今回の場合は「ばらつき(分散)の変化、大小関係、母分散が既知」で、二つの集団のばらつきの評価をするので、\(F\)分布の統計量\(F\)を使います。
さて、今回の帰無仮説は「母分散に対し、標本のばらつきに変化はない:\(σ^2 =1.0\)」で同じですが、対立仮説は「母分散に対し、標本のばらつきは大きくなった:\(σ^2\) >1.0」です。
今回の帰無仮説は「二つの集団のばらつきに違いはない:\(σ_A^2=σ_B^2\)」で同じですが、対立仮説は「集団Aが集団Bよりもばらつきが大きい:\(σ_A^2 > σ_B^2\)」です。
\[\]
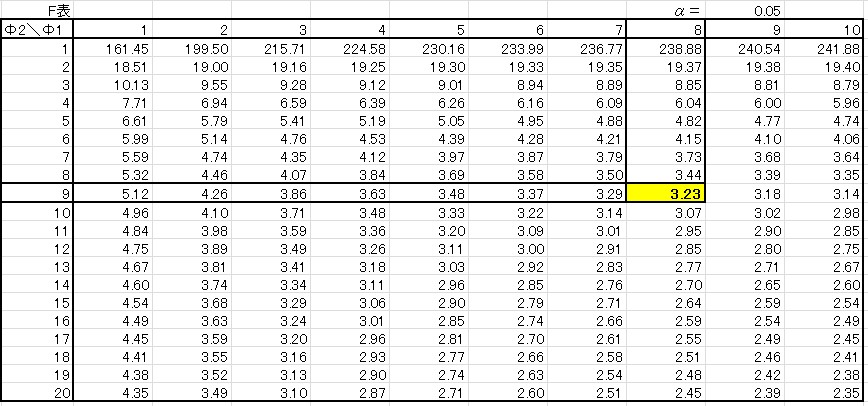
両側検定と片側検定では、棄却域が変わり、参考にする\(F\)表も変わります。結論から言うと、
\[\]
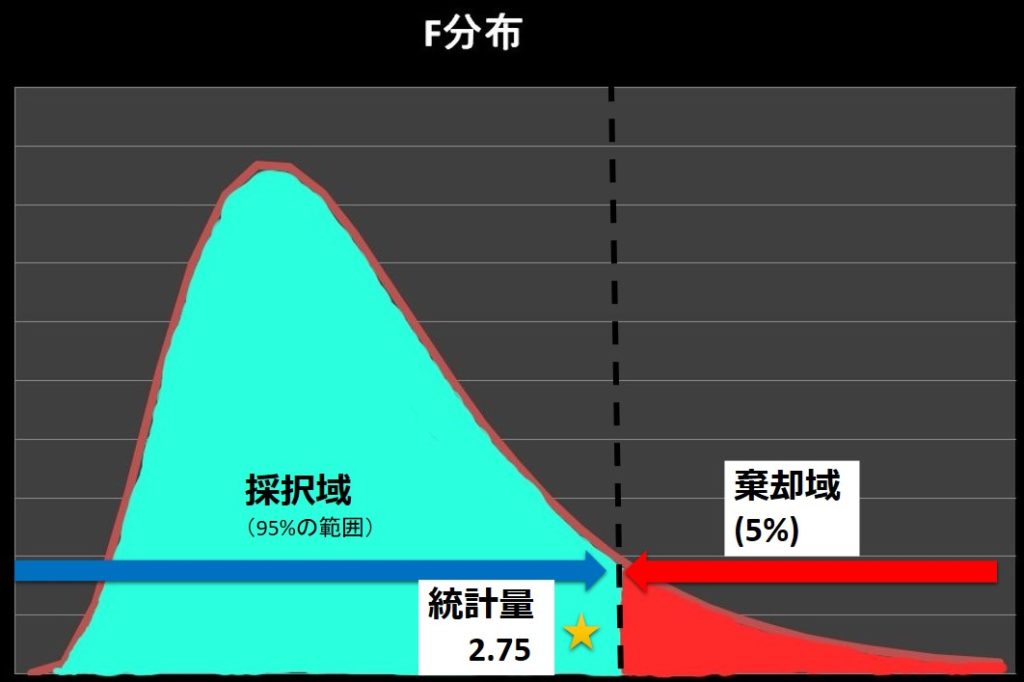
\[棄却限界値 F(Φ_1,Φ_2:0.05)=3.23 > 統計量 F_0 =2.75 \]
棄却限界値よりも統計量\(F_0\)の値が小さいので、統計量\(F_0\)は採択域内にあると判断します。
よって、帰無仮説の「二つの集団のばらつきに違いはない:\(σ_A^2=σ_B^2\)」が採択され、「ばらつきに違いがあるとは言えない」と判断します。
\[\]
まとめ
①\(F\)検定は二つの集団のばらつきを知りたいときに使う
②\(F\)表は該当する確率の表の自由度から読み取る
③\(F\)>1となるように検定統計量を設定し、分子の自由度が横軸\(Φ_1\)
④両側検定で下側の棄却限界値は「1 ÷ 棄却限界値 \(F\)(\(Φ_1,Φ_2:α/2\))」
⑤片側検定では、そのままの棄却限界値の確認Pは第一種の誤り\(α\)と同じ
\[\]
今回はF検定について学びましたが、一部疑問が生まれました。
\[棄却限界値 F(Φ_2,Φ_1:0.975)=\frac{1}{棄却限界値 F(Φ_1,Φ_2:0.025)}\]
次回はなぜこの式(F分布の下側棄却域)が成立するのかと、その意味を勉強しましょう。













[…] 記事「ばらつきに関する検定2:F検定」では、(F_0>1) となるように、分母と分子を入れ替える(設定する)と記載しました。 […]
[…] 次回は(F)検定について勉強していきましょう! […]
勉強中でよく理解できていない中での質問で恐縮ですが、両側検定の場合、棄却限界値は上側4.10。下側1/4.10。ということでしょうか?
ご質問ありがとうございます。
棄却限界値は今回の例題であれば、上側4.10 下側 1/4.10=0.244 となります。
F検定における棄却域の設定方法については、記事「F検定の下側(左側)棄却域の求め方」に書きました。
わかりにくい部分がありましたらご質問ください。
引き続き記事の改善にご協力いただければ幸いです。
これからも当ブログのご愛読をよろしくお願いします。
ご回答ありがとうございます。
当方の所有している参考書には、棄却限界値F(8,9:0.025)=4.10のとき、下側の棄却域を求める式はF(8,9:0.975)=1/(9,8:0.025)と解釈できるように記載がありましたので、1/4.36と理解しておりました。
[…] 次回からは、正規分布、t分布、(χ^2)カイ二乗分布、F分布のそれぞれの分布に対しての検定方法について、勉強していきましょう。 […]
当方、勉強中で理解がまだまだなのですが、
F分布において下側の値を求めるために逆数となることまでは理解できました。
このページの例題では、装置Aが9個、装置Bが10個で自由度はそれぞれ8、9となり、
下側F(8,9:0.975)~上側F(8,9:0.025)だと考え、下側はF(8,9:0.975)=1/(9,8:0.025)で計算しました。
しかし、ここではF(9,8:0.975)=1/(8,9:0.025)で計算し、答えとして下側F(9,8:0.975)~上側F(8,9:0.025)となっております。
これでは、下側と上側の自由度が異なり検定とはならない気がするのですが、大丈夫なのでしょうか?
ご質問ありがとうございます。
結論から言うと、「検定になるので、大丈夫です」。
ばらつきに関する検定では、二つ分布のばらつきの比を検定統計量として扱います。
二つ分布は同じデータ数(≒自由度)とは限らないため、二つの自由度から棄却限界値を決めます。
さて、二つの自由度から棄却限界値を決めるわけですが、二つの自由度の順番で棄却限界値が変わるのがF分布の特徴です。
二つの自由度の順番は、逆数になると順番が入れ替わりますが、「二つの自由度を使う」こと自体が変わるわけではありません。
つまり、下側と上側で“棄却限界値を決めるため”の自由度が異なるわけではありません。
昨日コメントさせていただいたものです。メールアドレスも生きていますし、荒らすつもりもありません。
例題の解答では、
下側F(9,8:0.975)=1/(8,9:0.025)=1/4.10=0.244~上側F(8,9:0.025)=4.10となっておりますが、
上の質問の方のように、
下側F(8,9:0.975)=1/(9,8:0.025)=1/4.36=0.229~上側F(8,9:0.025)=4.10にならないのは何故でしょうか?
当方の所有している参考書にも、下側F(8,9:0.975)=1/(9,8:0.025)と解釈できるように記載があります。
こちらのサイトを参考にQC検定を受験しようと考えておりますので、ご回答いただけると幸いです。
理由は、分子の不偏分散の自由度を8、分母の不偏分散の自由度を9として棄却限界値を”設定した”ためです。
ポイントは「どちらの分布を主として検定するか」です。
ばらつきに関する検定では、二つの分布の比を検定統計量として扱います。
F検定では、分子/分母が1よりも大きくなるように、自由度の順番を設定します。
今回の例題では、下側F(9,8:0.975)=1/(8,9:0.025)=1/4.10=0.244~上側F(8,9:0.025)=4.10 と考えます。
もし、下側F(8,9:0.975)=1/(9,8:0.025)=1/4.36=0.229~上側F(8,9:0.025)=4.10とすると、主となる分布が上側と下側で入れ替わってしまいます。
例えば、次の例を考えてみましょう。
テストの結果
チームA:50点、55点、60点、65点、70点
チームB:20点、40点、60点、80点、100点
このテストの結果のばらつきに対して、二つの解釈ができます。
①チームAはチームBよりもばらつきが小さい
②チームBはチームAよりもばらつきが大きい
このとき、①②ともに、ばらつきが大きい側と小さい側に棄却域を設定できます。
ただし、対象の分布を途中で変えると、正しい検定はできなくなってしまいます。
①を検定するのであれば、チームAがチームBよりもばらつきが小さいと判断できる最大値と最小値を棄却限界値とします。
チームAがチームBよりも小さいと判断できる最大値と、チームBがチームAよりも小さいと判断できる最小値で棄却限界値は設定しません。
これでは、検定の対象の分布が変わってしまい(主語が変わってしまい)、何に対する検定かあべこべになります。