管理図2　管理図の作り方

公開日2020年9月27日 　最終更新日 2023年1月22日

みなさんこんにちは、michiです。

前回は記事「管理図1 管理図とは」で管理図の概念と見方について学びました。

今回の記事では実際に管理図をどのように作るのか、その具体的な方法について学びます。

キーワード：「管理図」「計数表」「計量値ー計数値」

①\(\bar{x} – R\) 管理図の作り方

\(\bar{x} – R\)管理図は、計量値に使われる管理図になります。

群間変動を見るために\(\bar{x}\) 管理図を、郡内変動を見るために\(R\) 管理図を使用します。

すなわち、\(\bar{x} – R\) 管理図では、\(\bar{x}\) 管理図と\(R\) 管理図の2種類の管理図を使います。

それでは、下図のデータを基に\(\bar{x}\) 管理図と\(R\) 管理図を作ってみましょう。

このデータを見ると、群ごと（横方向）に各測定値、合計、平均値、範囲の順番で並んでいることが分かります。

※範囲\(R\) は、郡内の「最大値-最小値」で求められるばらつきを表す指標です。

\[\]

STEP1 中心線を求める　

\(\bar{x}\) 管理図における中心線は、各郡の平均値の合計を 群の数で割り、求められた群間の平均値になります。

上の例では、平均値の合計÷群の数 ⇒　\(1998.25 ÷ 20 = 99.9125\) となります。

\[\]

このイメージは、学校のテストで、ある1学級（群）の平均値を求め、その学級の属する学年の平均値を、全学級の平均値の合計値から計算することと同じになります。

\[\]

また、\(R\)管理図における中心線は、範囲の合計を群の数で割ることで求めます。

範囲の平均値を求めていると考えると、わかりやすいと思います。

先のデータでは、範囲の合計÷群の数 ⇒ \(138 ÷ 20 = 6.9\) となります。

\[\]

STEP2 \(\bar{x}\) 管理図の管理限界線を求める

\(\bar{x}\) 管理図における管理限界線は以下の式で表されます。

• 上方管理限界線　\(UCL = \bar{\bar{x}} +A_2×\bar{R} \)
• 下方管理限界線　\(LCL = \bar{\bar{x}} -A_2×\bar{R} \)

\(\bar{\bar{x}}\) は、郡内平均\(\bar{x}\) の合計から算出された平均値のことです。

\(\bar{R}\) はSTEP1で求めた範囲\(R\) の平均値のことです。

\(A_2\) は、・・・「\(\bar{x} – R\) 管理図用係数表」から求めます。（下図）

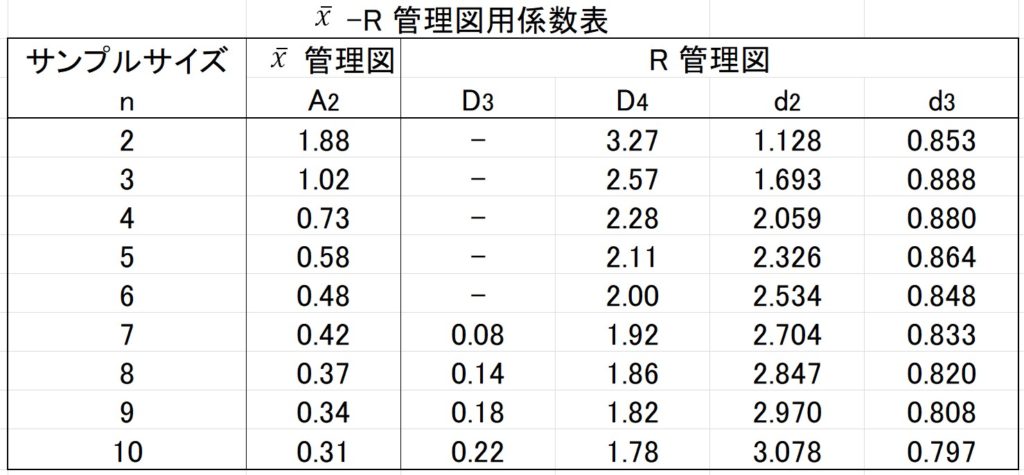
ポイントは、サンプルサイズによって\(A_2\) の値が変わることです。

サンプルサイズが増えるにつれ、係数の\(A_2\) の値が小さくなっています。

管理限界線の式から考えると、範囲の平均値\(\bar{R}\) が同じ条件では、係数\(A_2\) が小さくなると、上方・下方管理限界線は群間平均値\(\bar{\bar{x}}\) に近づくことが分かります。

これは、サンプルサイズが増えるにつれ、データのばらつきを抑えた測定ができるためです。

※表ではサンプルサイズ\(n=2\) から書かれていますので、見間違えないよう気を付けましょう。

\[\]

STEP3　\(R\) 管理図の管理限界線を求める

\(R\) 管理図における管理限界線は以下の式で表されます。

• 上方管理限界線　\(UCL = D_4 × \bar{R}\)
• 下方管理限界線　\(LCL = D_3 × \bar{R}\)

\(\bar{R}\) は先ほどと同じく範囲の平均値になります。

\(D_4, D_3\) についても、「\(\bar{x} – R\) 管理図用係数表」から求めることができます。

すると・・・

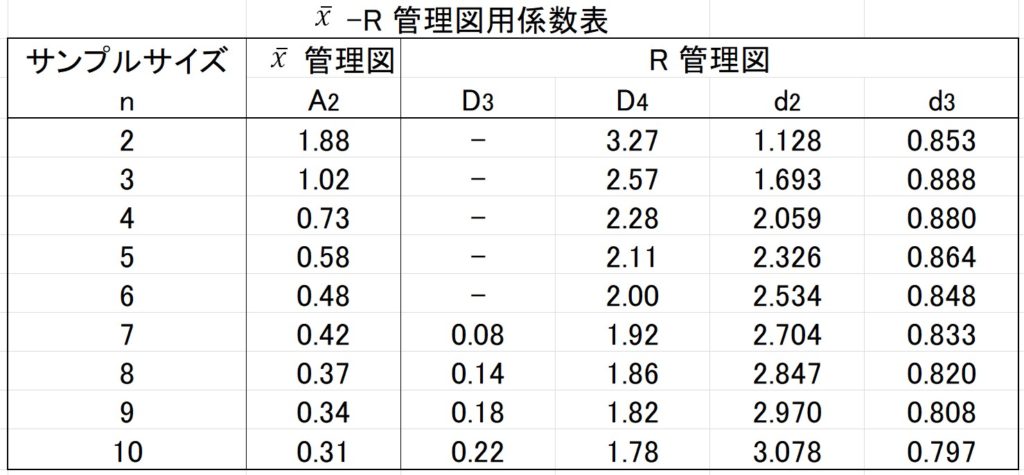
(。´･ω･)?

\(D_3\)は、サンプルサイズが6以下の時は数字が書かれていません！

そうなんです、\(R\)管理図では、サンプルサイズが6以下の場合、下方管理限界線は設定できません。（設定しません。）

\[\]

以上が\(\bar{x} – R\) 管理図の作り方ですが、\(\bar{x} – R\)管理図は、抽出したサンプルサイズが1より大きく、10以下の時(10未満の場合も)に使われます。

サンプルサイズが10よりも大きい場合は、\(\bar{x} – s\)管理図が使われます。

\(\bar{x} – s\)管理図は、QC検定1級の出題範囲になります。

また、サンプルサイズが1の場合は、\(x – R_s\)管理図が使われます。

\[\]

なお、「\(\bar{x} – R\) 管理図用係数表」に書かれている\(d_2\)は郡内の標準偏差\(σ_ω\) を求める際に使います。

群内の標準偏差\(σ_ω\) は、　\(σ_ω=\frac{\bar{R}}{d_2}\) で求めることができます。（めったに出題されませんが・・・）

\[\]

②\(\tilde{x}-R\) 管理図の作り方

\(\tilde{x}-R\) 管理図は、\(\tilde{x}\)の管理図と\(R\)の管理図を使用します。

※QC検定2級の出題範囲ではありませんが、実用性が高いので紹介します。

\[\]

\(\bar{x}\) 管理図とは異なり、中央値(\(\tilde{x}\)) を使用した管理図となります。

平均値ではなく中央値を使う場合は、平均値よりも中央値の方がデータの性質をよく表している場合に使用されます。

それでは、次のデータを基に\(\tilde{x}\)管理図と\(R\)管理図を作ってみましょう。

\[\]

STEP1　中心線を求める

\(\tilde{x}\) 管理図の中心線は、\(\tilde{x}\) の平均値（中央値の平均値）である\(\bar{\tilde{x}}\) になります。

上のデータから中心線を求めると、　\(2002.5 ÷ 20 = 100.125\)　となります。

このとき\(R\) 管理図の中心線は、\(\bar{x} – R\) 管理図で学んだ\(R\) 管理図と同じ(範囲の平均値)であることを覚えておきましょう。

\[\]

STEP２　\(\tilde{x}\) 管理図の管理限界線を求める

\(\tilde{x}\) 管理図における管理限界線は以下の式で表されます。

• 上方管理限界線　\(UCL = \bar{\tilde{x}} +m_3A_2×\bar{R} \)
• 下方管理限界線　\(LCL = \bar{\tilde{x}} -m_3A_2×\bar{R} \)

\(m_3A_2\) は、「\(\tilde{x}-R\)管理図用計数表」から求めます。（下図）

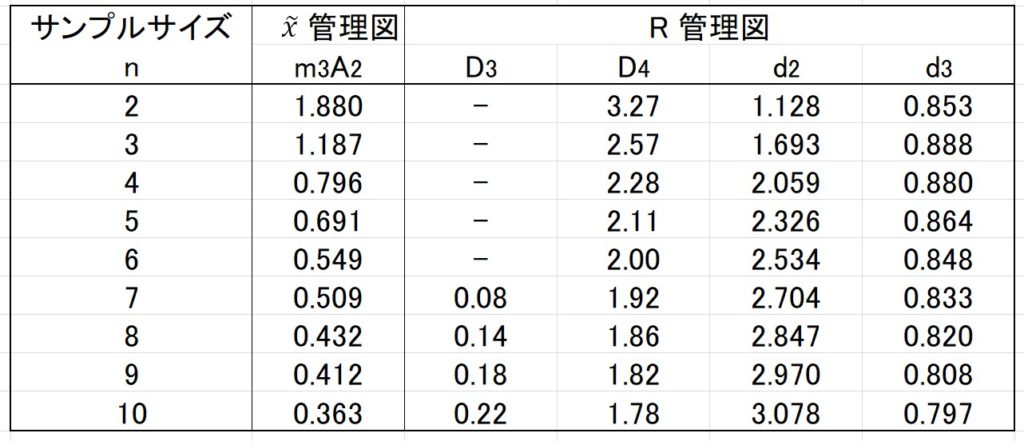
見方は、\(\bar{x}-R\) 管理図用計数表と同じです。

係数の\(m_3A_2\) は、\(A_4\)と書かれている場合もあります。

\[\]

STEP3 \(R\)管理図の管理限界線を求める

\(R\)管理図の管理限界線は、\(\bar{x} – R\) 管理図の時と同じく以下の式で表せされます。

• 上方管理限界線　\(UCL = D_4 × \bar{R}\)
• 下方管理限界線　\(LCL = D_3 × \bar{R}\)

説明の繰り返しになるので、説明は省きます。

詳細は、「①\(\bar{x} – R\) 管理図の作り方」の下の方を参照にしてください。

\[\]

③\(x-R_s\) 管理図の作り方

\(x-R_s\) 管理図は、サンプルサイズ\(n=1\) の時に使われる管理図になります。

※QC検定2級の出題範囲ではありませんが、実用性が高いので紹介します。

\[\]

破壊検査やサンプルを複数用意することが困難な工程における管理図として有効になります。

先ほど同様に下のデータを基に、管理図を作ってみましょう

\[\]

STEP1 中心線を求める

\(x\) 管理図の中心線は\(x\) の総和を群の数で割り、求めた平均値を中心線とします。

サンプルサイズ\(n=1\) のため、\(\bar{x}\) 管理図や\(\tilde{x}\) 管理図のように郡内での平均値や中央値を求めることができません。

また\(R_s\) 管理図のおける中心線は移動平均\(\bar{R_s}\) になります。

そもそも\(R_s\) とは「移動範囲」を表し、次の式で計算されます。

\[移動範囲(R_s)=|(i番目の測定値)-(i+1番目の測定値)| \]

「 \(|\qquad|\) 」は、絶対値を表します。

移動範囲に注目しているので、増加していようが減少していようが、重要なのはあくまでその大きさであることに気をつけてください。

各郡間の移動範囲の総和を求め、その総和を「群の数ー1」で求めます。

なぜ「－１」するのかというと、求めた移動範囲の総和は、各郡と次の群との差分の合計なので、データ数は、「群の数ー1」となるからです。

\[\]

STEP2 \(x\) 管理図の管理限界線を求める

\(x\) 管理図の管理限界線は次の式で求められます。

• 上方管理限界線\(UCL = \bar{x} + 2.66\bar{R_s}\)
• 下方管理限界線\(LCL = \bar{x} – 2.66\bar{R_s}\)

\(\bar{x}\) 管理図や\(\tilde{x}\) 管理図のようにサンプルサイズで変わる係数表を参照する必要はありません。

なぜなら、\(x\) 管理図のサンプルサイズは\(n=1\) で固定だからです。

\[\]

STEP3 \(R_s\) 管理図の管理限界線を求める

\(R_s\)管理図の管理限界線は、次の式で求められます。

• 上方管理限界線\(UCL = \bar{x} + 3.27\bar{R_s}\)
• 下方管理限界線\(LCL =\) 考えない！

下方管理限界線を「考えない！」とはどういうことでしょうか？

\[\]

\(R_s\) 管理図は移動範囲に対する管理図です。

つまり、下方管理限界線を設けるということは、群間で「一定以上のばらつきがなければならない」ということになります。

・・・まだ少しわかりづらいですね。

次の\(R\) 管理図をみてください。

\(R\) 管理図ではこの点の位置に対する管理図なのですが、\(R_s\) 管理図はこの点の差に対する管理図となります。

つまり、\(R_s\) 管理図に下方管理限界線を設けた場合、同じ品質で作ったものは異常となってしまうのです。

\[\]

④\(np\) 管理図の作り方

計量値に対する管理図として、「\(\bar{x}-R\) 管理図、\(\tilde{x}-R\) 管理図、\(x-R_s\)管理図」を学びました。

今度は計数値に対する管理図を学んでいきます。

\(np\) 管理図は不良個数に対する管理図となります。

\[\]

計数値に対する管理図は計量値に対する管理図と異なり、「ばらつき」に相当する\(R\) または\(R_s\) 管理図がありません。

「ばらつき」というのは郡内の変動のことを意味するのですが、\(np\) 管理図と\(p\)管理図で注目するのは群間の「不適合品」の数に変化がないかを管理します。

つまり、ロット毎に不適合品の数に変化がないかを管理するわけです。

前置きが長くなりましたが、作り方をみてみましょう。

\[\]

STEP1 中心線を求める

\(np\) 管理図の中心線は、「不良個数の総和 を群の数 で割り」求めます。

平均してどの程度の不良品数があるかを計算しています。

関係式は以下のようになります。

\[n\bar{p}=\frac{不良個数の総和}{群の数}\]

\[\]

STEP２　管理限界線を求める

\(np\) 管理図の管理限界線は、次の式で求められます。

• 上方管理限界線\(UCL=n\bar{p}+3\sqrt{n\bar{p}(1-\bar{p})}\)
• 下方管理限界線\(LCL=n\bar{p}-3\sqrt{n\bar{p}(1-\bar{p})}\)

急に複雑な式がでてきて、やる気がなくなりそうですが、式の意味を考えてみます。

まず「+,ー」の符号の前の\(n\bar{p}\) ですが、これは中心線を意味します。

さて、\(\sqrt{n\bar{p}(1-\bar{p})}\) ですが、これは二項分布の標準偏差を表します。

詳細は記事「二項分布の考え方」をご参照ください。

※分散が\(np(1-p)\) なので、標準偏差は\(\sqrt{np(1-p)}\) となります。

\[\]

すると、「管理限界線＝不良個数の平均±3×標準偏差」　が成立します。

\[\]

⑤\(p\) 管理図の作り方

\(p\) 管理図は不良率に対する管理図となります。

不良率というと、計量値と考えてしまいそうですが、そうではありません。

なぜなら、不良率は「計数値÷計数値」で求められるからです。

計数値同士の掛け算や割り算は計数値となります。

\[\]

STEP1 中心線を求める

\(p\) 管理図の中心線は以下の式で求められます。

\[\bar{p} = \frac{不良個数の総和}{検査個数の総和（総データ数)}\]

ちょっと何言ってるかわかりませんね。

\[\]

ここで、\(np\) 管理図と比較してみましょう。

\(np\) 管理図の中心線は以下の式でした。

\[n\bar{p}=\frac{不良個数の総和}{群の数}\]

\(np\) 管理図は平均して一つの群にどの程度の不良品があるかを管理しました。

さて、\(n\) はサンプルサイズのことでしたから、次のように式変形できます。

\[n\bar{p}=\frac{不良個数の総和}{群の数}\qquad ⇒\bar{p} = \frac{不良個数の総和}{群の数×サンプルサイズ n} \]

分母の「\(群の数×サンプルサイズ n\)」 は、データ数（=検査個数）の総和を意味します。

つまり、\(np\) 管理図も、\(p\) 管理図も本質的には同じもので、サンプルサイズ\(n\) がどこにあるかの違いでしかありません。

\[\]

STEP2 管理限界線を求める

\(p\) 管理図の管理限界線は、以下の式で求められます。

• 上方管理限界線\(UCL=\bar{p}+3\sqrt{\frac{\bar{p}(1-\bar{p})}{n}}\)
• 下方管理限界線\(LCL=\bar{p}-3\sqrt{\frac{\bar{p}(1-\bar{p})}{n}}\)

また複雑な式が出てきて嫌な感じですが、中心線と同様に\(np\) 管理図の管理限界線と比較すると、

• 上方管理限界線\(UCL=n\bar{p}+3\sqrt{n\bar{p}(1-\bar{p})}\)
• 下方管理限界線\(LCL=n\bar{p}-3\sqrt{n\bar{p}(1-\bar{p})}\)

・・・

\[p管理図の管理限界線=np管理図の管理限界線÷n(サンプルサイズ)\]

が成り立ちます。

まさしく中心線と同じ考え方で、「\(np\)管理図を\(n\) で割っただけ」になります。

\[\]

では、わざわざサンプルサイズ\(n\) で割った管理図を考えるメリットは何でしょうか？

(。´･ω･)?

答えの一つは、「率で考えることができるから」です。

例えば製品Aが、部品B20個、部品C100個、部品D200個で作られているとします。

率で考えた場合、構成している数は違えど、どの部品の品質低下が、製品Aの品質低下の主要因であるか判断しやすくなります。

また、率で考えるため、サンプルサイズが群ごとに異なっていても、管理図を作って管理することが可能になります。

\[\]

⑥\(c\)管理図の作り方

\(c\) 管理図は大きさが一定のサンプルにおける不適合数に対する管理図になります。

不適合数は欠点数と言ったほうが理解しやすいかもしれません。

\(p\) 管理図と\(np\) 管理図は不適合品数に対する管理図ですので、定義が違います。

不適合品数と不適合数の違いを理解するために次の例題を考えてみましょう。

\[\]

例）あるライターのAさんは毎日1000文字のレポートを5枚書いている。

20日間で100枚のレポートを作成したが、10枚のレポートに誤字や脱字があった。

誤字や脱字のあったレポートには、平均して5カ所のミスがあった。

この時、不適合品数（今回の場合は、誤字や脱字があったレポート数）は、10枚になります。

しかし、不適合数（欠点数）は5カ所×10枚＝50カ所　となります。

\[\]

さて、少し前置きが長くなりましたが、不適合数(欠点数)に対する管理図である\(c\) 管理図の作り方を学びましょう。

\[\]

STEP1　中心線を求める

\(c\) 管理図における中心線は以下の式で表されます。

\[\bar{c}=\frac{欠点数の総和}{群の数}\]

すなわち、一つの群あたりの平均欠点数を求めます。

\[\]

STEP２　管理限界線を求める

\(c\) 管理図の管理限界線は次の式で求められます。

• 上方管理限界線\(UCL=\bar{c}+3\sqrt{\bar{c}}\)
• 下方管理限界線\(LCL=\bar{c}-3\sqrt{\bar{c}}\)

\[\]

\(np\) 管理図、\(p\) 管理図に比べると、ずいぶん簡単な式になりました。

\(c\)管理図では、欠点数の表れ方をポアソン分布に近似して考えます。

ポアソン分布では、分散は　\(λ\)　で表されます。

\(c\)管理図においては、\(\bar{c} =λ\)　となります。

\[\]

\(\sqrt{\bar{c}}\) が標準偏差を表すので、やはり「管理限界線＝中心線±3×標準偏差」が成立します。

※標準偏差が\(\sqrt{\bar{c}}\) となる理由は、記事「ポアソン分布について」をご参考ください。

\[\]

⑦\(u\) 管理図の作り方

いよいよ最後です。

\(u\) 管理図は大きさが異なるサンプルにおける不適合数の管理図となります。

「\(np\) 管理図－\(p\) 管理図」における関係が、「\(c\) 管理図－\(u\) 管理図」における関係に当てはまります。

つまり、\(u\) 管理図は不適合率に対する管理図となります。

それでは、管理図の作り方を見てみましょう。

\[\]

STEP1 中心線を求める

中心線は以下の式で求めることができます。

\[\bar{u}=\frac{欠点数の総和}{サンプルの大きさの総和}\]

すなわち、サンプルサイズ全体からみて、単位サンプルサイズ当たりの欠点数が中心線となります。

\[\]

STEP2　管理限界線を求める

\(u\) 管理図における管理限界線は以下の式で表されます。

• 上方管理限界線\(UCL=\bar{u}+3\sqrt{\frac{\bar{u}}{n}}\)
• 下方管理限界線\(UCL=\bar{u}-3\sqrt{\frac{\bar{u}}{n}}\)

平方根の中身は、中心線に当たる\(\bar{u}\) をサンプルサイズ\(n\) で割っています。

これは単位サンプルサイズ当たりの欠点数を、そのサンプルサイズで割ることで、分散（\(√\)で標準偏差）を求めています。

やはり管理限界線においても、「\(np\) 管理図ー\(p\) 管理図」の関係が成立します。

\[\]

まとめ

①群間変動は\(\bar{x}\) 管理図、郡内変動は\(R\) 管理図

②\(\bar{x}-R\) 管理図の\(\bar{x}\)を中央値\(\tilde{x}\)にしたのが\(\tilde{x}-R\) 管理図

③\(x-R_s\) 管理図は、サンプルサイズ\(n=1\)の時の管理図

④\(np\) 管理図は不適合品数に対する管理図

⑤\(p\) 管理図は不適合品率に対する管理図

⑥\(c\) 管理図は不適合数に対する管理図

⑦\(u\) 管理図は不適合率に対する管理図

\[\]

以上が管理図に関する内容でした。

管理図はQC検定2級だけでなくQC検定3級にも出題されます。

また、実用性もかなり高い知識ですので、しっかり身につけましょう。

次回は、信頼性工学について勉強していきます。

⇒オススメ書籍はこちら

⇒サイトマップ