分割表を使った検定　１

公開日2020年6月14日 　最終更新日 2022年1月10日

こんにちは、michiです。

前回までは二項分布とポアソン分布の検定・推定を学びました。

今回は分割表による検定を学びます。

キーワード：「分割表」「観測度数」「期待度数」

①分割表の検定統計量

分割表の検定統計量は以下の式で表されます。

\[χ^2=\displaystyle \sum_{i=1}^m \sum_{j=1}^n \frac{(f_{ij}-e_{ij})^2}{e_{ij}} \]

\(f_{ij}\):観測度数、\(e_{ij}\):期待度数

(。´･ω･)?

そうですね、意味わかんないし、使い方もわかりませんよね。

この記事では使い方について説明していきます。

\[\]

まず、この式を見てわかることは、\(χ^2\)があることがわかります。

検定統計量が\(χ^2\) ということは、ばらつきの違いを検定していることになります。（詳細は記事「ばらつきに関する検定1:カイ二乗検定」をご参考ください。）

また、\(f_{ij}\):観測度数、\(e_{ij}\):期待度数という言葉が出てきました。

「度数」とは、「各階級での観測値の個数」を意味します。

この階級は、分析内容によって分析者が設定します。

\[\]

例えばサイコロの目は1～6まであるので、それぞれの目を階級とすれば6個の階級ができます。

このサイコロを60回投げた時の1の目がでる度数の予測値は10になります。

言い換えると、60回サイコロを投げた時に1の目が出る回数の期待値は10回となります。

この期待される度数を「期待度数」といい、実際にサイコロを60回投げた時に観測された1の目の出た回数を「観測度数」といいます。

\[\]

②ピアソンの適合基準

分割表の検定統計量について学ぶ前に、そのベースとなるものがあります。

それが「ピアソンの適合度基準」といい、下の式で表されます。

\[χ^2=\displaystyle \sum_{i=1}^k \frac{(f_i-np_i)^2}{np_i} \]

\[\]

※なぜこの検定統計量が使われ、\(χ^2\)分布に従うのかは説明がすごく長くなるので、次回にします。

ピアソンの適合度基準を冒頭の分割表の検定統計量と比較すると、次のことが分かります。

\[χ^2=\displaystyle \sum_{i=1}^m \sum_{j=1}^n \frac{(f_{ij}-e_{ij})^2}{e_{ij}} \]

1. どちらも\(χ^2\)が検定統計量
2. \(∑\)の数が違う
3. 期待度数\(e_{ij}\) ⇒ \(np_i\) になっている

といったところでしょうか。

①どちらも\(χ^2\)が検定統計量

このことから、ピアソンの適合度基準も分割表の検定統計量も「ばらつきの違い」を検証していることが分かります。

何のばらつきか違いかというと、「観測した数（＝観測度数）」と「期待される数（＝期待度数）」になります。

②\(∑\)の数が違う

この差は属性の数の差なのですが、分割表では行と列で二つの属性を表現しているため、\(∑\)が二つになります。

※属性≒グループと考えてください。

③期待度数\(e_{ij}\) ⇒ \(np_i\) になっている

「度数」とは、「各階級での観測値の個数」といいました。

\(np_i\)は何を意味するのでしょうか？

(。´･ω･)?

実は\(np_i\)も本質的には度数を表しています。

なぜなら、\(np_i\)= 全体の数\(n\)× ある事象の発生確率\(p_i\)　だからです。

以上のことから、ピアソンの適合度基準をまとめると、

\[χ^2=\displaystyle \sum_{i=1}^k \frac{(f_i-np_i)^2}{np_i} \]

\[=\displaystyle \sum^{全階級} \frac{(測定度数-期待度数)^2}{期待度数} \]

\[\]

分子を二乗している理由は、マイナスがあると全階級で足し算をしたときに、ばらつきが消しあい小さくなってしまうためです。

この考え方は平方和の考え方と一緒ですね。

このピアソンの適合度基準を言葉で表すと、「1度数あたりの測定度数と期待度数の差の二乗を全階級にわたって足した合計」となります。

これは別の言い方では「相対度数」といわれます。

\[\]

③ピアソンの適合度基準の実例

なんとなくピアソンの適合度基準の数式の意味は理解できましたでしょうか？

実例を解いて確認してみましょう。

問）サイコロを60回投げた時の結果は下表のようになった、この時のピアソンの適合度基準から、\(χ^2\)検定を実施してみよう。有意水準を5%とする。

さて、この結果を\(χ^2\)検定し、理論値からずれているかを検証します。（結果は明らかですが・・・）

この時の帰無仮説は「サイコロの目の出方は理論値と差がない」です。

サイコロの目の出る確認\(p\)は \(\frac{1}{6}\) でどの目も同じはずれす。

ですので、各目の期待度数は \(np=60×\frac{1}{60} =10\)　になります。

よって検定統計量\(χ^2\)の値は

\[χ^2=\displaystyle \sum_{i=1}^k \frac{(f_i-np_i)^2}{np_i}\]

\[=\frac{(0-10)^2}{60×\frac{1}{6}}+\frac{(5-10)^2}{60×\frac{1}{6}}+・・・+\frac{(30-10)^2}{60×\frac{1}{6}}\]

\[=55\]

この時の自由度は 5 (=6-1)　ですので、\(χ^2\)表を見ると・・・

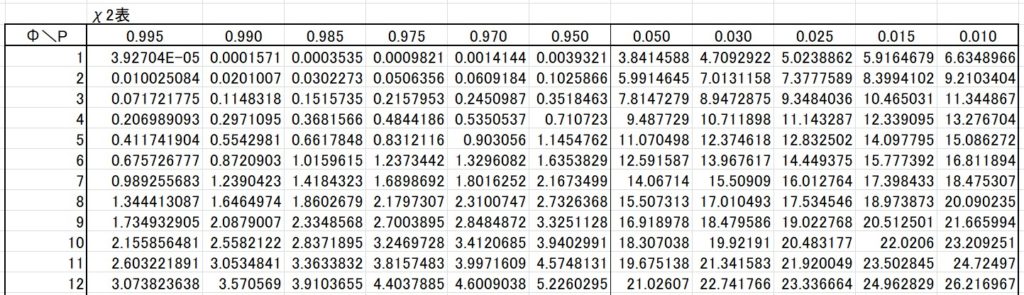
_(:3｣∠)_　もっとわかりやすくしてよ・・・

表より　\(χ^2=55 > 　χ^2(5,0.05)=11.0705　\) 　となります。

よって、帰無仮説である「サイコロの目の出方は理論値と差がない」という仮説は棄却され、サイコロの目の出方は理論値と異なる　となります。

\[\]

④分割表を使ったの検定

ピアソンの適合度基準は一つの属性（グループ）に対して使えるものでした。

これを分割表でも使えるように二つ属性に対して結果を得るにはどうすればよいのでしょうか？

ピアソンの適合度基準を振り返ると、

\[χ^2=\displaystyle \sum_{i=1}^k \frac{(f_i-np_i)^2}{np_i} \]

\[\]

単純ですが\(Σ\)を足して、属性が二つになったので、\(np_i ⇒np_i・p_j\)とすればよさそうです。

※\(np_i\)個に確率\(p_j\)を掛け、\(p_i\)かつ\(p_j\)の個数をもとめています。

\[χ^2=\displaystyle \sum_i \sum_j \frac{(f_{ij}-np_i・p_j)^2}{np_i・p_j}\]

\[χ^2=\displaystyle \sum_i \sum_j \frac{(f_{ij}-f_i・f_j/n)^2}{f_i・f_j/n}\]

この時の\(f_i,f_j\)を周辺度数といい、相対度数による推定値に置き換えられます。

関係式は、\(p_i=\frac{f_i}{n}\)、\(p_j=\frac{f_j}{n}\)　になります。

これと期待度数\(e_{ij}\) との関係は、\(e_{ij}=f_i・f_j/n\) になります。　よって、

\[χ^2=\displaystyle \sum_{i=1}^m \sum_{j=1}^n \frac{(f_{ij}-e_{ij})^2}{e_{ij}} \]

\(f_{ij}\):観測度数、\(e_{ij}\):期待度数

\[\]

なぜわざわざ \(p_i,p_j\) を \(f_i,f_j\) に変換するのでしょうか？

それは、分割表に書かれる数字は 確率\(p\) ではなく、 周辺度数\(f\) であることが一般的だからです。

ちょっと実感がわかないかもしれません、実例をあげて考えてみましょう。

\[\]

⑤分割表を使った検定：例題

さて、分割表の例として以下の問題を考えます。

問）サイコロを一回投げると同時にコインを投げる試行を60回行った結果、下表（表1）の結果となった。

この時、分割表の検定統計量をもとめ、検定を行ってみよう。

有意水準は5%としてね

\[\]

問題を解く前に、簡単に分割表のミカタを学びましょう。

まず右下の60という数字ですが、これが全試行回数になります。

この60回の試行を「コインの表or裏」で集計したのが、60の上（縦）の数字になります。この時はサイコロの目は気にしません。

次に、60回の試行を「サイコロの目1～6」で集計したのが60の左（横）の数字になります。この時はコインの表or裏は気にしません。

\[\]

そして、「コインの表or裏」で集計したものは「サイコロの目1～6」で集計した結果にそれぞれ分割します。

※「サイコロの目1～6」で集計したものは「コインの表or裏」で集計した結果に分割します。

この時に下表の黄色の範囲内の数字が実際に観測された数字ということになります。

どうでしょうか？

実際に観測されたデータをそれぞれ全合計数で割り算し、確率を求めたいでしょうか？

ｬﾝ♪(´･ω･｀pq)三(pq´･ω･｀)ｬﾝ♪

エクセルなら苦も無くできますが、やらなくていいなら、やりたくないですよね。

というか、QC検定ではエクセル禁止です。

\[\]

ちょっと脱線したので、分割表の検定統計量を思い出しましょう。

\[χ^2=\displaystyle \sum_{i=1}^m \sum_{j=1}^n \frac{(f_{ij}-e_{ij})^2}{e_{ij}} \]

\[χ^2=\displaystyle \sum_i \sum_j \frac{(f_{ij}-f_i・f_j/n)^2}{f_i・f_j/n}\]

\(f_{ij}\) は\(i\) と \(j\) の二つの属性から決まる数字なので、先のような二次元の分割表では、ただ一つの値にきまします。

例えば、\(f_{4,表} =6\)　　となります。

では、\(f_i\) は何でしょうか？

この時は\(f_j\)に指定がありませんので、\(f_i\) 全部ということになります。

つまり、\(f_4 = 6+4 = 10\)　となります。

同様に、\(f_j\)は、\(f_i\) 全部にあてはまるので、

\(f_表 = 0+3+4+6+7+18 = 38\) となります。

全試行回数 \(n=60\) ですから、サイコロの目が4で、かつコインが表の時の検定統計量\(χ’^2\)は、

\[χ’^2 \qquad= \frac{(f_{ij}-f_i・f_j/n)^2}{f_i・f_j/n} = \frac{(6-38・10/60)^2}{38・10/60} \]

\[=0.0175439 \]

\[\]

この計算を「コインの表or裏」×「サイコロの目1～6」=12　の全パターンでやり、合計を求めます。

下表の黄色の範囲内全部やるってことです。

よって計算式は・・・

\[χ^2 = \frac{(0-38・0/60)^2}{38・0/60}+ \frac{(3-38・5/60)^2}{38・5/60}+・・・+\frac{(12-22・30/60)^2}{22・30/60}\]

\[=1.0047847\]

\[\]

全体の計算は面倒なのでエクセルでやりました。

|壁|*ﾟдﾟ)ﾅﾆ?

先ほども述べたように、QC検定でエクセルは使えませんが、電卓は使えるので、試験本番は気合いで頑張りましょう。

\[\]

それでは、先ほど求めた検定統計量\(χ^2\)を検定します。

この時の分割表の自由度は、（コインの面の数-1）×（サイコロの目数-1）　となります。

※自由度の詳細は記事「平方和ではだめ？不偏分散とは」をご参考ください。

表より　\(χ^2\)= 1.0048< \(χ^2\)(5,0.05)=11.0705 　となります。

帰無仮説について定義をしていませんでした、この時の帰無仮説は「コインの表裏の出方で、サイコロの目の出方に違いがない」です。

\[\]

先ほどの計算結果より、検定統計量は棄却域内にあると判定されるため、帰無仮説は採択され、「コインの表裏の出方で、サイコロの目の出方に違いがあるとは言えない」となります。

\[\]

ヾﾉﾟ∀ﾟ*)ィﾔィﾔィﾔィﾔ!!

そうですね、ツッコミたくなりますよね。

もう少しこの分割表の検定について考えてみます。

\[\]

⑥分割表の検定の本質

④の例題で考えた分割表をもう一度見てみましょう。

この表をみて率直に思うことは、

「サイコロめっちゃ偏ってんじゃん」か、「コイン表出すぎワロタ」　ですね。

はい、まず間違いなくサイコロはめっちゃ偏ってますし、コインワロタです。

しかし、分割表で判定するのは「サイコロめっちゃ偏ってるか否か」でも、「コイン表出すぎワロタ」でもありません。

(。´･ω･)?　ドユコト？

\[\]

分割表の検定における帰無仮説は、「コインの表裏の出方で、サイコロの目の出方に違いがない」　でした。

具体的に言うと、「コインが表の時は6の目がでやすく、コインが裏の時も6の目がでやすい」ため、コインの出方とサイコロの目の出方は関係ないということになります。

重要なのは「コインの表裏の出方とサイコロの目の出方」の相関関係になります。

\[\]

もう少し例を挙げてみましょう。次の分割表を見てください。

この表は、④で計算した分割表のコインの裏の結果が真逆になっています。

この時の検定統計量\(χ^2\) を計算すると、\(χ^2 = 34.5386\) となります。

よって、\(χ^2= 34.5386\) > \(χ^2(5,0.05)=11.0705\)　となるため、

帰無仮説は棄却され、「コインの表裏の出方で、サイコロの目の出方に違いがある」となります。

この検定結果は、「コインが表の時は6の目がでやすく、コインが裏の時は1の目がでやすい」と判定したことになります。

つまり、コインの出方とサイコロの目の出方に相関があるということです。

\[\]

以上をまとめると、分割表の検定の本質は「属性Aの結果と属性Bの結果に相関関係があるか否か（違いがあるか否か）」となります。

サイコロがめっちゃ偏ってようが、コインワロタだろうが、それらは分割表の本質的な検定ではないので、気をつけましょう！

\[\]

\[\]

⑦分割表の検定が片側検定の理由

分割表について学んできましたが、疑問点があります。

「なぜ片側検定なのか？」です。

(。´･ω･)?

その答えは「観測度数と期待度数が近い場合は、棄却域にならないため」です。

(;´･ω･)？？？

どういうことか、考えていきましょう。

\[\]

分割表の検定統計量は \( χ^2 \) 分布に従います。

\( χ^2 \) 分布 では右に行くほど検定統計量が大きくなります。

検定統計量が大きいとは何を意味するのでしょうか？

(-ω-;)ウーン

\[\]

分割表の場合、検定統計量が大きいとは「観測度数と期待度数の差が大きい」ことと同じ意味になります。

※正確には、

\[=\displaystyle \sum^{全階級} \frac{(測定度数-期待度数)^2}{期待度数} \]

です。

\[\]

では、検定統計量が小さい場合はどうでしょうか？

検定統計量が小さい場合は、「観測度数と期待度数が近い」という意味になります。

※ \( χ^2 \) 分布 一番左の検定統計量が 0 の時は、すべての観測度数が期待度数と同じときの値です。

\[\]

分割表による検定では、出方に違いがないかを検定します。

出方とは、観測度数と期待度数の差のことです。

\[\]

もし両側検定を行うと、左側の棄却域は「観測度数は期待度数に近すぎるため、出方に違いがある」となります。

つまり、期待されていた値と観測された値が近いと、観測された値は期待された値とは出方が違うということです。

(ヾﾉ･ω･`)ﾅｲﾅｲ

分割表の検定で、左側の棄却域を設定する両側検定を行うと、このように矛盾が生じてしまいます。

\[\]

分割表を使った検定では、片側検定それも右側の棄却域のみを考えてください！

\[\]

まとめ

①分割表の検定統計量は\(χ^2\) を使う

②ピアソンの適合基準では、確率で考える

③ピアソンの適合基準は、測定結果と理論値との差を検定

④分割表では、ピアソンの適合基準の確率⇒周辺度数　で考える

⑤分割表の計算は、期待度数を求めればなんとかなる

⑥分割表の本質は、二つのデータの相関関係

⑦分割表の検定は片側検定で、右側の棄却域のみを考える！

\[\]

今回は内容盛りだくさんでした。

次回はなぜ分割表の検定統計量が\(χ^2\)になるのかを学びましょう！

⇒オススメ書籍はこちら

⇒サイトマップ