超幾何分布 とは

公開日2021年8月29日 最終更新日 2021年9月26日
みなさんこんにちは、michiです。
前回はQCストーリーについて学びました。
今回からはQC検定の統計的な話をしていこうと思います。
今回は超幾何(ちょうきか)分布についてです。
キーワード:「有限母集団」
目次
①超幾何分布とは
超幾何分布とは、有限母集団からの非復元抽出を行ったときの分布です。
超幾何分布における出現確率(\(x\)を引く確率) は、以下の計算式で計算できます。
\[P(x)=\frac{\scriptsize{M}\large{C}\scriptsize{x} \quad \large{×}\quad \scriptsize{N-M}\large{C}\scriptsize{n-x} }{\scriptsize{N}\large{C}\scriptsize{n}}\]
- 有限母集団内の総数 \(N\) 個
- 不適合品の総数 \(M\) 個
- 抜き取った個数 \(n\) 個
- 抜き取った個数の内不適合品の数 \(x\) 個
\[\]
(。´・ω・)?
また、超幾何分布分布の期待値と分散は次の式で表されます。
\[期待値E(x)=\frac{nM}{N}\]
\[分散V(x)=\frac{nM}{N}(1-\frac{M}{N})(\frac{N-n}{N-1})\]
\[\]
(;´・ω・)???
数式を書いていきましたが、まず冒頭の言葉の意味を考えてみます。
「有限母集団からの非復元抽出」
これは、「総数が決まっている有限母集団からサンプルを抽出し、抽出したサンプルを元の有限母集団に戻さずに次のサンプルを抽出する。」という意味になります。
\[\]
具体例を考えてみましょう。
例えばお祭りのくじ引きを考えるとわかりやすいです。
くじ引きにイカサマがなければ、外れくじをドンドン引いていけば、当たりくじを引く確率は上昇していきますよね。
あとは、モンティ・ホール問題なんかも有名ですが、それはまたの機会にしましょう。
それでは、超幾何分布のイメージがわかったので、数式の理解をしていきましょう!

\[\]
②超幾何分布の確率計算式の意味
超幾何分布のイメージがわかったので、もう一度確率の式を見てみましょう。
\[P(x)=\frac{\scriptsize{M}\large{C}\scriptsize{x} \quad \large{×}\quad \scriptsize{N-M}\large{C}\scriptsize{n-x} }{\scriptsize{N}\large{C}\scriptsize{n}}\]
- 有限母集団内の総数 \(N\) 個
- 不適合品の総数 \(M\) 個
- 抜き取った個数 \(n\) 個
- 抜き取った個数の内不適合品の数 \(x\) 個
\[\]
大文字の \(\large{C}\) は、Combination の意味で、頭文字の \(C\) をとっています。
Combinationでは、次の関係式が成り立ちます。
\[\scriptsize{N}\large{C}\scriptsize{n}=\frac{N!}{n!(N-n)!}\]
「!」は階乗の意味です。
階乗は、その数字よりも小さい数字をすべて掛け合わせます。
例えば「5!」ならば、 「5!=5×4×3×2×1」 となります。
\[\]
さて、\(\scriptsize{N}\large{C}\scriptsize{n}\) の意味ですが、
「N個で構成される母集団から、n個のサンプルを抽出したときの組み合わせの数」 になります。
超幾何分布では、この\(C\) が三つも出てきます。
「\(\scriptsize{M}\large{C}\scriptsize{x}\)」「\(\scriptsize{N-M}\large{C}\scriptsize{n-x}\)」「\(\scriptsize{N}\large{C}\scriptsize{n}\)」です。
それぞれの意味が理解できれば、超幾何分布の確率の数式の意味が理解できそうです。
\[\]
1)\(\scriptsize{M}\large{C}\scriptsize{x}\)
まず分子の \(\scriptsize{M}\large{C}\scriptsize{x}\) について考えます。
\(M\) は有限母集団の全不適合品数であり、\(x\)は抽出したサンプル内の不適合品数になります。
つまり \(\scriptsize{M}\large{C}\scriptsize{x}\) は、母集団の中にある全不適合品数 \(M\) 個から、\(x\) 個の不適合品を抽出するときの組み合わせの数 になります。

\[\]
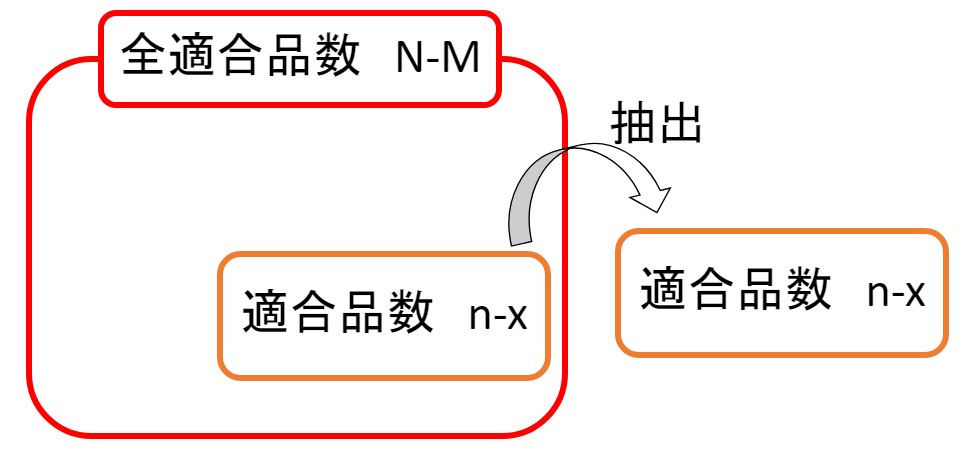
2)\(\scriptsize{N-M}\large{C}\scriptsize{n-x}\)
次に分子のもう一つのCombination \(\scriptsize{N-M}\large{C}\scriptsize{n-x}\) について考えます。
Nは要素の数、つまり、適合品も不適合品も含めた有限母集団の要素すべてとなります。
なので \(N-M\) は、「有限母集団の要素数-全不適合品数=全適合品数」 となります。
有限母集団全体から全不適合品数を引くと、残るのは適合品数だけという理屈ですね。
\[\]
同様に、\(n-x\)についても考えます。
\(n\)は抽出したサンプル数、\(x\)は抽出したサンプル内の不適合品数です。
なので \(n-x\) とは、「抽出したサンプル数ーサンプル内の不適合品数=サンプル内の適合品数」 となります。
\[\]
以上のことから\(\scriptsize{N-M}\large{C}\scriptsize{n-x}\) は、母集団内の全適合品数 (\(N-M\)) 個から、 (\(n-x\)) 個の適合品を抽出する組み合わせ となります。
\[\]
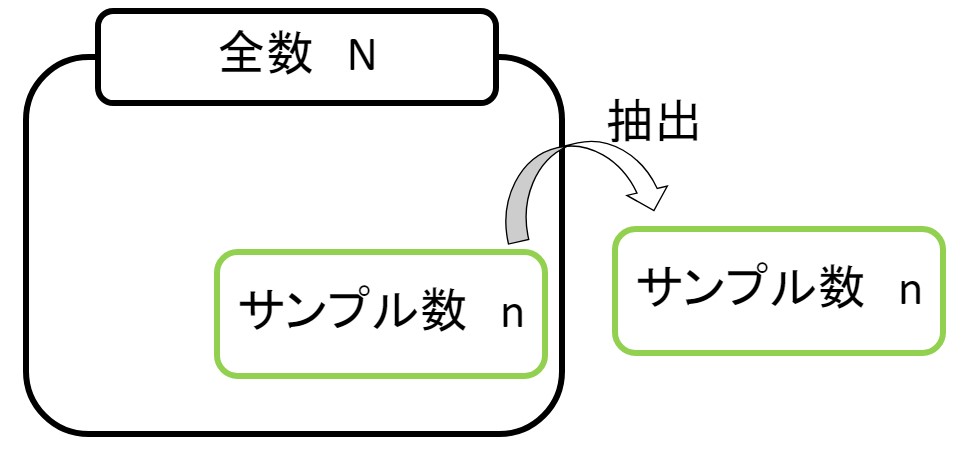
3)\(\scriptsize{N}\large{C}\scriptsize{n}\)
最後に分母の \(\scriptsize{N}\large{C}\scriptsize{n}\) について考えます。
いままでの説明を理解していると、簡単ですね。
\(\scriptsize{N}\large{C}\scriptsize{n}\) は、要素数が\(N\) 個の有限母集団から \(n\) 個のサンプルを抽出する組み合わせになります。
\[\]
4)確率計算式の意味
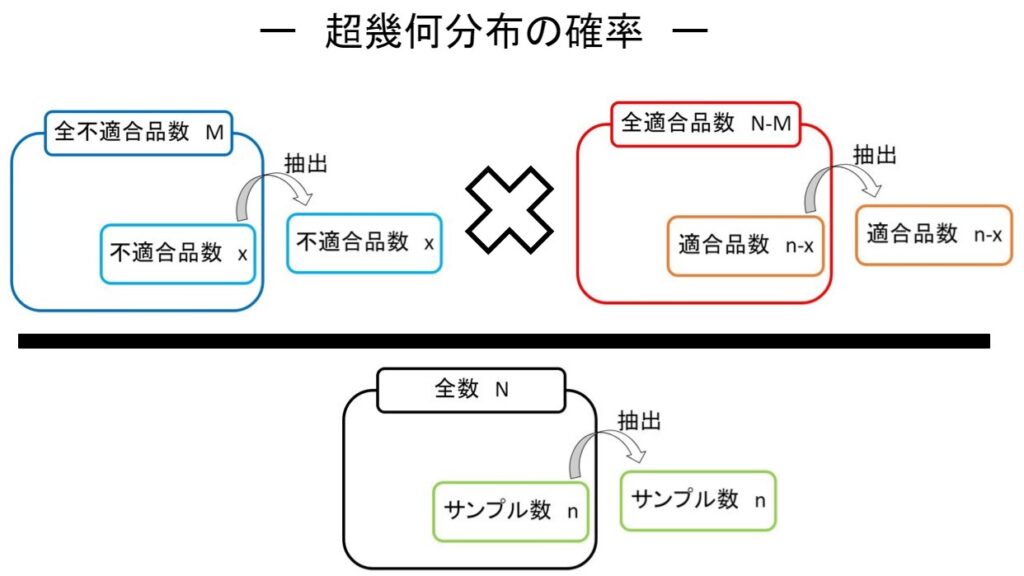
三つのCombination の意味がわかったので、超幾何分布の確率計算式の意味を考えてみます。
\[P(x)=\frac{\scriptsize{M}\large{C}\scriptsize{x} \quad \large{×}\quad \scriptsize{N-M}\large{C}\scriptsize{n-x} }{\scriptsize{N}\large{C}\scriptsize{n}}\]
- 要素の数 \(N\) 個
- 不適合品数 \(M\) 個
- 抜き取った個数 \(n\) 個
- 抜き取った個数の内不適合品の数 \(x\) 個
\[\]
まず分子の \(\scriptsize{M}\large{C}\scriptsize{x} \quad \large{×}\quad \scriptsize{N-M}\large{C}\scriptsize{n-x}\) です。
これは、1)、2)でも理解したように、有限母集団内の全不適合品数 \(M\) 個から \(x\) 個の不適合品を抽出し、かつ、有限母集団内の全適合品数 \(N-M\) 個から \(n-x\) 個の適合品を抽出する組み合わせ になります。
\[\]
分母の \(\scriptsize{N}\large{C}\scriptsize{n}\) は、3)で学んだように、\(N\) 個の有限母集団から \(n\) 個のサンプルを抽出する組み合わせになります。
つまり超幾何分布の確率計算式は、すべての有限母集団からサンプルを抽出する組み合わせを分母に、 \(x\) 個の不適合品と \(n-x\) 個の適合品を抽出する組み合わせを分子とする ことで計算される確率となります。
\[\]
③超幾何分布の期待値と分散
超幾何分布の期待値と分散は、次の式で表されます。
\[期待値E(x)=\frac{nM}{N}\]
\[分散V(x)=\frac{nM}{N}(1-\frac{M}{N})(\frac{N-n}{N-1})\]
- 有限母集団内の総数 \(N\) 個
- 不適合品の総数 \(M\) 個
- 抜き取った個数 \(n\) 個
\[\]
このとき、分散の式にでてくる係数 (\(\frac{N-n}{N-1}\)) を有限修正(有限母集団修正)といいます。
有限修正とは、(無限母集団を想定した)二項分布で計算した分散の値を、超幾何分布に適応するために使います。
\[\]
お祭りのくじ引きで例えると、
くじであたりを引く確率は、「くじが無限にある場合は二項分布に従うが、くじが有限の場合は超幾何分布に従う」ということを意味します。
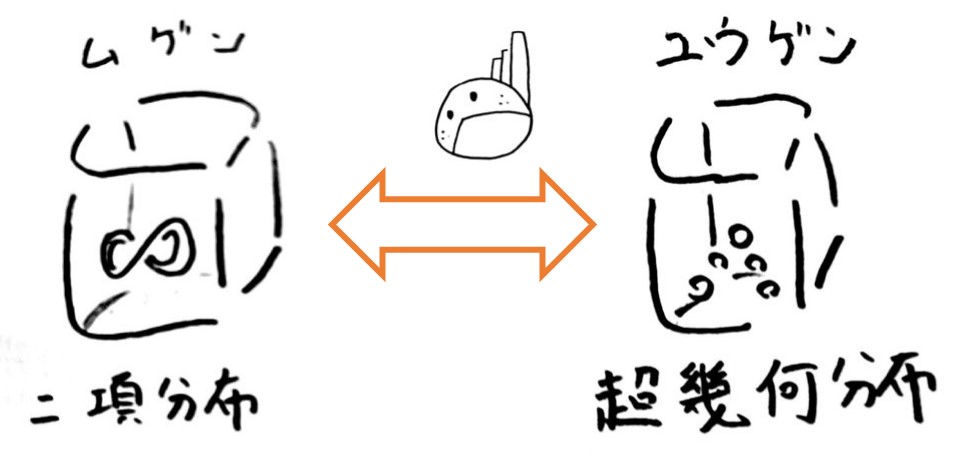
ここで、二項分布というキーワードがでてきました。
二項分布と超幾何分布の関係性について考えてみましょう。
\[\]
④超幾何分布と二項分布の関係
超幾何分布の期待値と分散をもう一度見てみましょう。
\[期待値E(x)=\frac{nM}{N}\]
\[分散V(x)=\frac{nM}{N}(1-\frac{M}{N})(\frac{N-n}{N-1})\]
- 有限母集団内の総数 \(N\) 個
- 不適合品の総数 \(M\) 個
- 抜き取った個数 \(n\) 個
\[\]
まず注目すべきは、 \(\frac{M}{N}\) です。
この分数は何を表すのでしょうか?
(。´・ω・)?
\[\]
分母が有限母集団内の総数で、分子が不適合品の総数になるので、有限母集団から不適合品を抽出する確率になります。
二項分布ではこれを \(p\) としました。
超幾何分布でも \(\frac{M}{N}\) ⇒ \(p\) として、超幾何分布の期待値と分散の式を書き直してみます。
\[期待値E(x)=np\]
\[分散V(x)=np(1-p)(\frac{N-n}{N-1})\]
\[\]
なんか見覚えのある形になってきました。
二項分布の期待値と分散は次の式で表されます。
\[期待値E(x)=np\]
\[分散V(x)=np(1-p)\]。
\[\]
分散の有限修正 (\(\frac{N-n}{N-1}\)) だけが、超幾何分布と二項分布の違いになります。
超幾何分布を二項分布に近似するときは、\(N\) ⇒ ∞ とする必要があります。
つまり、有限母集団を無限集団とみなすことで、近似ができることになります。
現実にはないと信じたいですが、外れくじがどんどん投入されるお祭りのくじ引きをイメージしてください。

\[\]
有限母集団を無限母集団とみなすことができる、というのは次のように解釈することができます。
いくら抜き取っても母数への影響は無視でき、次に抜き取るときの確率は何ら変わらない。
では、実用的にはどのくらいの母数に対し、どの程度抜き取っても影響がないと言えるのでしょうか?
(。´・ω・)?
\[\]
実用的には、 (\(\frac{n}{N} ≦ 0.10\)) と言われています。
具体的に言うと、母集団が100個で抜き取り本数が10個程度なら、超幾何分布を二項分布に近似できます。
この時の有限修正を計算してみると、
\[\frac{N-n}{N-1}=\frac{100-10}{100-1}=\frac{90}{99}=0.9090…\]
となります。
超幾何分布の分散は、二項分布の分散の約91%の値になります。
実用的には、このくらいの誤差は二項分布にしちゃおうってことです。
もちろん、どの程度精度が必要かによって、この近似をよしとするかは変わってきます。
\[\]
⑤超幾何分布とポアソン分布の関係
さて、二項分布ときくとポアソン分布も思い出しますよね。
※ポアソン分布の詳細は、記事「ポアソン分布について」をご参照ください。
\[\]
二項分布をポアソン分布に近似できる条件は、 \(\frac{x}{n}≦0.10\) です。
つまり抽出したサンプルの内、不適合品の数が \(\frac{1}{10}\) (10%)以下であれば、二項分布をポアソン分布に近似しちゃおうってことでした。
\[\]
まとめると、有限母集団の10%以下が抜き取り本数であれば超幾何分布を二項分布に近似でき、抜き取り本数の10%以下が不適合品数であれば、二項分布をポアソン分布に近似できるということです。
よって、超幾何分布をポアソン分布に近似するには、「少なくとも」母集団の1%以下の不適合品数である必要があります。
「少なくとも」を強調している理由は、抽出するサンプル数\(n\)が、(\(\frac{n}{N} ≦ 0.10\)) を満たす必要があるためです。

※ ≒ は近似を表します。
\[\]
まとめ
①超幾何分布とは、有限母集団からの非復元抽出を行ったときの分布
②超幾何分布の確率計算式は
\[P(x)=\frac{\scriptsize{M}\large{C}\scriptsize{x} \quad \large{×}\quad \scriptsize{N-M}\large{C}\scriptsize{n-x} }{\scriptsize{N}\large{C}\scriptsize{n}}\]
- 有限母集団内の総数 \(N\) 個
- 不適合品の総数 \(M\) 個
- 抜き取った個数 \(n\) 個
- 抜き取った個数の内不適合品の数 \(x\) 個
③超幾何分布の期待値と分散は
\[期待値E(x)=\frac{nM}{N}\]
\[分散V(x)=\frac{nM}{N}(1-\frac{M}{N})(\frac{N-n}{N-1})\]
- 有限母集団内の総数 \(N\) 個
- 不適合品の総数 \(M\) 個
- 抜き取った個数 \(n\) 個
④超幾何分布の母集団が無限母集団とみなせるなら、二項分布に近似できる
⑤超幾何分布が二項分布に近似できて、不適合品率が10%以下ならポアソン分布にも近似できる
\[\]
流石QC検定1級の試験範囲という感じで、難しくなってきました。
有言母集団という考え方は、より実践的な考え方です。
ぜひ実務で使ってみましょう!
\[\]















はじめまして。
QC検定2級の時にお世話になり、合格できました。
ありがとうございます☆
さらに上の級があるのに受けない選択肢はなく、1級の勉強を始めたのはいいのですが、商業高校卒で数学の知識もなくて苦戦しています。
おまけに1級は分かりやすいテキストもなく、諦めようかと思っていたところへmichiさんの記事が1級へと進んでいることに気づきました!
もう少し頑張ろうと思います。
期待しています。◕‿◕。
QC検定2級合格おめでとうございます!
1級は受験を諦めてしまう人もいる中で素晴らしい志です!
1級の試験範囲は広く、わかりやすいテキストも見つからない状況です。
このブログが少しでも多くの人の役に立つよう、少しずつではありますが記事を更新していきます。
期待に応えられるように頑張ります!