Welch(ウェルチ)の検定 とは

公開日2021年12月1日 最終更新日 2021年12月6日
みなさんこんにちは、michiです。
前回は判断の誤りと検出力、p値について勉強しました。
この記事ではQC検定2級の記事で取り上げなかった検定について、紹介していきます。
今回はWelchの検定です。
キーワード:「Welch」「等価自由度」

目次
①Welchの検定とは
Welchの検定とは、2つの母平均の差に関する検定で、2つの集団の分散 \(\sigma_1^2\) 、\(\sigma_2^2\) が未知で、かつ分散が同じ \(\sigma_1^2= \sigma_2^2 \) かどうかわからない場合に行われれる検定です。
(。´・ω・)?
一言で言えば、「t検定の亜種!」
2つの集団の分散はわからないけど、 平均値の差 を検定したいときに使います。
\[\]
検定統計量\(t_0\) は、
\[t_0=\frac{\bar{x_1}- \bar{x_2} }{\sqrt{\frac{V_1}{n_1}+\frac{V_2}{n_2}}}\]
- \(\bar{x_1}\) :”集団1″の平均値
- \(\bar{x_2}\) :”集団2″の平均値
- \(V_1\):”集団1″の分散
- \(V_2\):”集団2″の分散
- \(n_1\):”集団1″の標本数
- \(n_2\):”集団2″の標本数
です。
\[\]
この時、棄却限界値の設定に使う等価自由度 \(\phi^*\) は、次式で表されます。
\[ \phi^* =\frac{\left(\frac{V_A}{n_A}+\frac{V_b}{n_B}\right)^2}{\frac{\left(\frac{V_A}{n_A}\right)^2}{\phi_A}+\frac{\left( \frac{V_B}{n_B}\right)^2 }{\phi_B}}\]
(´・ω・`)
わかりにくいので、式変形をします。
\[\frac{\left(\frac{V_A}{n_A}+\frac{V_b}{n_B}\right)^2 }{\phi^*}= \frac{\left(\frac{V_A}{n_A}\right)^2}{\phi_A}+\frac{\left( \frac{V_B}{n_B}\right)^2 }{\phi_B} \]
(´;ω;`)
…さて、等価自由度 \(\phi^*\) ですが、通常は整数になりません。
等価自由度の計算はサタースウェイト(Satterthwaite)の方法で計算できます。
「Welchの検定」の等価自由度は、エクセルの”データ分析”を使う場合は自動で計算してくれます。
\[\]
さて、Welchの検定の検定統計量\(t_0\) をみてください。
\[t_0=\frac{\bar{x_1}- \bar{x_2} }{\sqrt{\frac{V_1}{n_1}+\frac{V_2}{n_2}}}\]
この値とt検定の検定統計量を比較してみます。
※t検定の詳細は記事「平均値に関する検定2:t分布 t検定」をご参考ください。
\[\]
t検定の検定統計量を\(t_0’\) とすると、
\[t_0’=\frac{\bar{x}-\mu_0}{\sqrt{\frac{V}{n}}}\]
\(\mu_0\) は測定値などの特定の値です。
母集団との比較であれば、 \(\mu_0\) は母平均となります。
\[\]
Welchの検定と比較します。
分子は2つのの集団の平均の差なので、本質的には同じ意味です。
分母はWelchの検定では \(\sqrt{\frac{V_1}{n_1}+\frac{V_2}{n_2}}\) なのに対し、t検定では\(\sqrt{\frac{V}{n}}\) となっています。
2つの検定における分母の違いが生じる原因は、「分散が同じかどうかわからない」ためです。
検定の対象となる2つの集団の分散(ばらつき)が同じかどうかわからないため、分母は \(\sqrt{\frac{V_1}{n_1}+\frac{V_2}{n_2}}\) で計算します。

\[\]
それでは、もし2つの集団のばらつきが同じ場合はどうなるのでしょうか?
(。´・ω・)?
分散(ばらつき)は同じなので、\(V_1=V_2=V\) としましょう。
すると、Welchの検定統計量の分母は、 \(\sqrt{V\left({\frac{1}{n_1}+\frac{1}{n_2}}\right)}\) となります。
分散(ばらつき)が同じだけでは、t検定の検定統計量 \(\sqrt{\frac{V}{n}}\) と同じ式になりません。
※この時の検定統計量 \(t_0”\)は、データに対応のない場合のt検定の検定統計量となります。
\[t_0”=\frac{\bar{x}-\mu_0}{\sqrt{V\left({\frac{1}{n_1}+\frac{1}{n_2}}\right)}}\]
\[\]
t検討の検定統計量との違いは、母集団と比較しているのか、2つの集団を比較しているのかです。
t検定における検定統計量\(t_0’\) は、
\[t_0’=\frac{\bar{x}-\mu_0}{\sqrt{\frac{V}{n}}}\]
です。
この式に出てくる \(\bar{x}\)、\(V\)、\(n\) は標本から得られた平均値、不偏分散、標本数です。
母集団から得られるデータは、母平均 \(\mu_0\) のみとなります。
t検定においては、母集団の大きさが標本数よりも大きいため、標本集団のばらつきのみを考慮すればよいです。
\[\]
Welchの検定において、ばらつきが同じ二つの集団の検定統計量の分母は以下の式で表されます。
\[\sqrt{V\left(\frac{1}{n_1}+\frac{1}{n_2}\right)}\]
上式で\(n_1\) が標本数、\(n_2\) が母集団の数として考えてみます。
母集団の数(\(n_2\)) は、標本数(\(n_1\)) に比べてかなり大きい数とします。
すると、先ほどの分母の式は、
\[\sqrt{V\left(\frac{1}{n_1}+\frac{1}{n_2}\right)} ⇒ \sqrt{V\left(\frac{1}{n_1}+\frac{1}{\infty}\right)} \approx \sqrt{\frac{V}{n_1}} \]
となります。
\[\]
このようにWelch検定の検定統計量は、片方の集団を母集団とみなすことで、t検定の検定統計量と一致することがわかります。
最後に、Welchの検定統計量をおさらいしましょう。
\[t_0=\frac{\bar{x_1}- \bar{x_2} }{\sqrt{\frac{V_1}{n_1}+\frac{V_2}{n_2}}}\]
\[\]
②等価自由度\(\phi^*\) の計算方法
Welchの検定における自由度は整数にならないと書きました。
では、どうやってt値(\(\phi^*,\alpha\)) を計算すれば良いのでしょうか?
(。´・ω・)?
一つめの方法は、エクセルを使います。
エクセル関数「T.INV.2T(両側確率,自由度)」 を使い、計算します。

\[\]
ただし両側確率で計算しているので、確率の設定には気をつけてください。

※t値の注意点は、記事「平均値に関する検定2:t分布 t検定」を参考にしてください。
\[\]
普段の業務は、Excelが使えるので問題はないでしょう。
しかし、試験ではそうはいきません。
(*´∀`)ゞそかそか
Excelが使えない場合は、補間で求めます。
ヾ(・ω・`;)ノぁゎゎ
\[\]
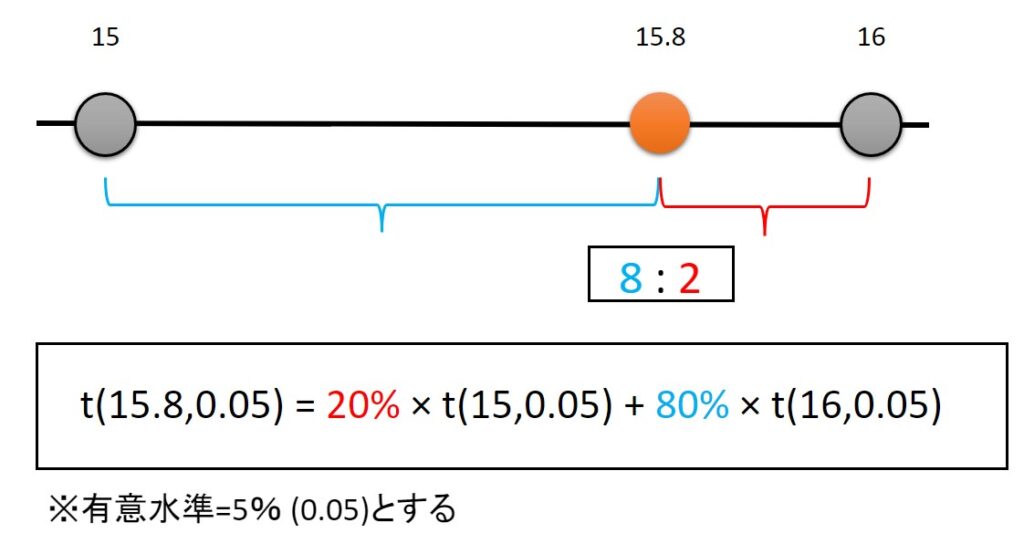
例えば、等価自由度 \(\phi^*=15.8\) と計算できたとします。
有意水準\(\alpha\)=5% とすると、知りたいt値は \(t(15.8,0.05)\) となります。
※Excelの計算式と順番が違うので注意!
\[\]
t表には整数しか書かれていないため、等価自由度「\(15.8\)」はt表からは求められません。
そこで、等価自由度\(\phi^*=15.8\) の前後の整数のt値から補間して考えます。
補間では\(t(15,0.05)\) と \(t(16,0.05)\) を使います。
実際に計算してみましょう。
\[t(15.8,0.05)=(1-0.8)\times t(15,0.05)+0.8\times t(16,0.05)\]
\[=0.2\times 1.753+0.8\times 1.746\]
\[=1.7474\]
\[\]
このように、等価自由度 \(\phi^*=15.8\) を自由度15と自由度16のt値を比で計算します。
等価自由度 \(\phi^*=15.8\) の場合は、\(t(15,0.05)\)の値の20%と \(t(16,0.05)\)の値の80%の数値を足して、15.8の値として補間して考えます。
\[\]
\[\]
③Welchの検定の利用
Welchの検定は、2つの母平均の差に関する検定で、2つの集団のばらつきが未知、かつ同じかどうかも判断できない場合に使用します。
実はかなり利用する機会が多い検定です。
ΣΣ(゚Д゚;)
\[\]
例えば、みかん農家がある1日に採れたみかんの重さの平均値についてt検定をした場合を考えます。
ここで問題になるのは、母平均の設定です。
去年1年間で採れたみかんのデータを母平均とすれば、データ数も問題なく確かにt検定はできそうです。
\[\]
しかしこの母平均では、みかんが旬の時期もそうでない時期も同じ母平均に含まれます。
さらに言うと、日当たりの良い場所・悪い場所も同じ母平均に含まれます。
\[\]
\[\]
もし検定したい”ある1日のデータ”が、日当たりの良い場所で採れた、旬の時期のみかんの重さの平均値とします。
去年1年間を母平均としたt検定検定の結果は、「差がある(平均値は上がった)」となったとします。
この検定結果だけで考えると、「去年よりもみかんの出来が良い!」と結論を出してしまいます。
しかし、それは早合点と言えます。
σ( ・ω-;)ウーン…
今回のみかんの例では、できるだけ同じ条件の集団と比較しなければ、適切な判断ができません。
去年と同じ日・同じ場所・同じ木で採れたみかんのデータと比較するわけです。
そうなると、母集団という大きなグループと標本との比較(t検定)というよりも、同じ大きさの集団間の比較(Welchの検定)が適しています。
Welchの検定では集団間のばらつきがあることも考慮して検定するため、同等程度のばらつきが想定できない場合でも有効です。
(∩・∀・)∩オォ!
\[\]
今回はみかんで例えましたが、機械的な部品であっても製造装置の経年劣化などで、ばらつきが変化する可能性があります。
ばらつきが変わる可能性を考慮すると、やはりWelchの検定が実用的であることがわかります。
\[\]
まとめ
①Welchの検定は、二つの母平均の差に関する検定(分散が不明)
②Welchの検定では、等価自由度っていうのを使う
③Welchの検定は守備範囲が広い!
\[\]
今回はWelchの検定について学びました。
Excelを使えば実務への適用も簡単です。
今回学んだことを是非実践で活かしてみましょう!
\[\]













[…] 前回はウェルチの検定について勉強しました。 […]