公開日2021年5月22日 最終更新日 2021年5月29日
みなさんこんにちは、michiです。
前回の記事「【実践 2】管理図」に引き続き、今回はQC検定実践編として、相関関係について考えていきます。
相関関係の分析についての詳細は記事「相関関係1 相関係数とは」をご参照ください。
この記事を読めば、QC検定1級の論述対策になる!…カモ
キーワード:「相関係数」「因果関係」
目次
①散布図の作成
まずは散布図を作成し、異常値がないかなど大まかな情報整理を行います。
散布図は目的変数1つと説明変数1つが対応するように作成します。
一つ目的変数に対して複数の説明変数を考えたい場合は、面倒ですが複数散布図を作成しましょう。
\[\]
よくグラフを3D化する人がいますが、オススメしません。
これは、散布図に限らず、円グラフや棒グラフにも言えることなのですが、3D化するとデータを正確にとらえづらくなるからです。
例えば、次の円グラフを見てください。
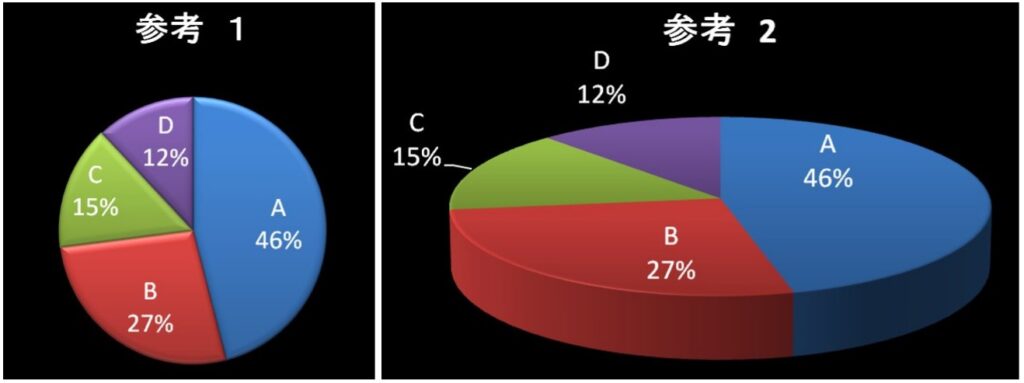
どちらも基データは一緒なのですが、3D化している右の方が要因Aと要因Bの割合が全体に対して大きいように錯覚してしまいます。
\[\]
数値が書いてあるから大丈夫だろう! って意見もあるかもしれません。
しかし、なぜグラフを作成するのでしょうか?
(。´・ω・)?
それは話し手が、聞き手に正確に情報を伝えたいからのはずです。
であれば、誤解を招くおそれのある表現は避けるべきでしょう。
\[\]
②近似直線の導入
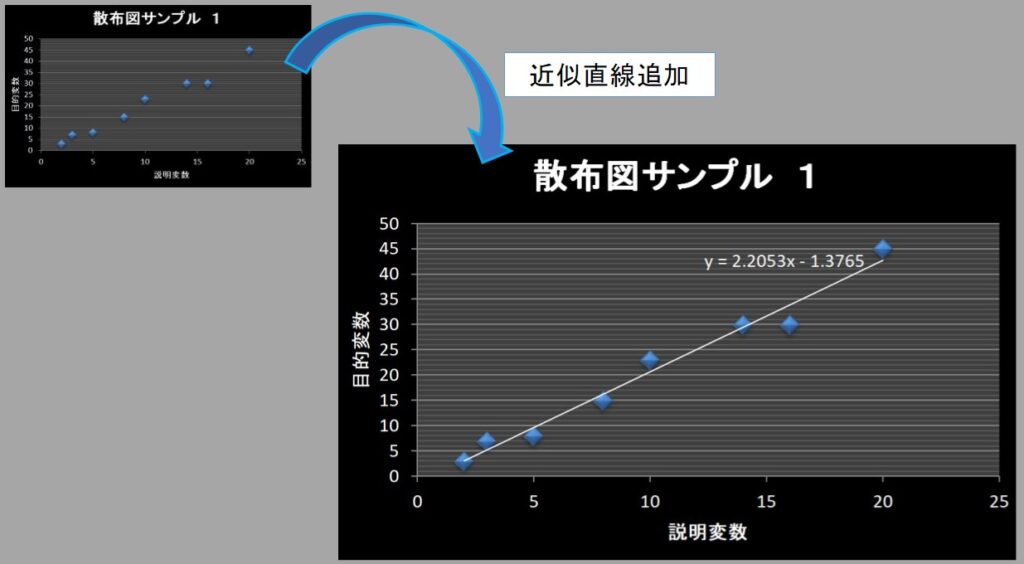
散布図が作成できたら、近似直線をグラフに追加しましょう。
近似直線を追加することで、データの分布の傾向が分かります。
\[\]
この近似直線はデータの回帰直線になることも理解しておきましょう!

\[\]
③相関係数を求める
相関係数\(r\) は記事「相関関係1 相関係数とは」にも書いたように、次の式で表されます。
\[r=\frac{S_{xy}}{\sqrt{S_x}×\sqrt{S_y}}\]
\[\]
この計算式をエクセルに打ち込むのは少々面倒ですよね。
さらに、数式の入力ミスもしてしまいそうです。
ウ・・・ウン((・ω・`;))
\[\]
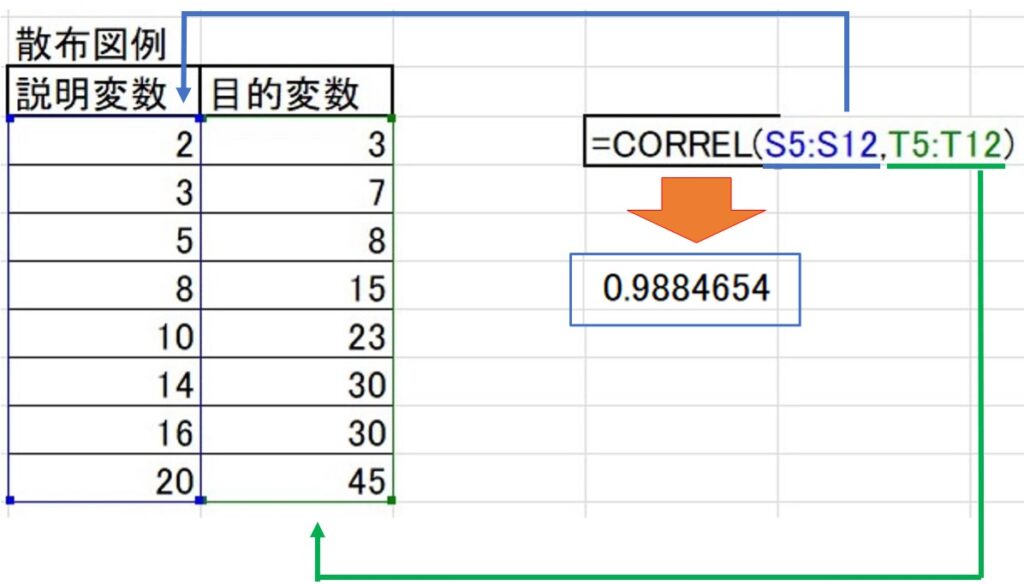
そこでエクセル関数「CORREL」を使います!
すると、次のようにあっさりと相関係数が求められてしまいます。
\[\]
④指数分布の場合は対数変換
実践編の記事「【実践 1】工程能力指数とヒストグラム」「【実践 2】管理図」でもおなじみの指数分布です。
次のデータをそのまま散布図にしてみましょう。


(;´・ω・)
この時点でもう嫌な予感がしますが、エクセル関数「CORREL」を使うと相関係数\(r\)は「0.624」となります。
一応弱い相関があるといえそうです。
\[\]
ちなみに散布図に近似直線を引くと、下の図のようになります。

近似直線からみると外れ値(異常値)が多いように見えます。
特に、20番目の値はかなり離れていますよね。
\[\]
さて、説明変数(横軸)はそのままに縦軸を対数変換してみましょう。
すると先ほどの散布図は次のようになります。

対数変換前のデータと比較すると、目的変数に対して説明変数が線形に変化していることが分かります。
この対数変換後の散布図に近似曲線をいれてみます。

ここでの注意点は、近似直線ではなく近似曲線をいれることです。
説明変数を対数変換しているため、近似直線を入れると”曲線”になってしまします。
\[\]
図の話はここまでにして、対数変換後のデータに対して、相関係数をエクセル関数「CORREL」を使って求めてみます。

すると、相関係数の値は「0.951」となります。
Σ(・ω・ノ)ノ!
これは強い相関があるといえそうです。
\[\]
基データは同じなのに相関係数に差が出てしまいました。
この相関係数の差は、基データが回帰直線に従うと判断したか、回帰(指数)曲線に従うと考えたかの違いになります。
説明変数と目的変数の関係を考えて、必要であれば変換したデータを使って相関係数を求めましょう!
\[\]
※今回は対数変換を例にしましたが、二次関数変換や逆数変換など状況に応じていろいろ試してみましょう!
╭( ・ㅂ・)و̑ グッ
\[\]
⑤相関係数の分析
最後に相関係数の分析をしましょう。
一般的に相関家関係の有無は下表のように表されます。
[表]
この時に気をつけることは、
- 相関係数がゼロだからといって、相関がないとは限らない
- 相関係数が高いからといって、相関があるとは限らない
- 相関関係があるからといって、因果関係があるとは限らない
①と②はそんなこと言われたら、分析も何もないじゃん…って気もしますね。
それでは一つずつ解説していきます。
\[\]
①相関係数がゼロだからといって、相関がないとは限らない
いきなりですが、次の散布図を見てください。

この散布図で表されているデータ(目的変数ー説明変数)の相関係数は「0.139」です。
つまり、勉強時間とテストの点に相関関係はない…はずです。
念のため、このデータを表でまとめてみました。

σ(・ω・,,`)?アレ?
先ほどの散布図をAさんとBさんで層別してみます。

青色がAさん、赤色がBさんのプロットした結果です。
勉強時間に対して、Aさんは負の相関、Bさんは正の相関があることが分かります。
もしかしたらAさんは勉強しすぎて、試験本番で緊張しちゃうタイプなのかもしれませんね。
\[\]
このように、層別すれば相関関係があるのに、AさんとBさんを一緒にしてしまったために相関関係がないと判断してしまうことがあります。
このような場合「全体で見れば相関がない」と考えるか、「人によって差がある」と考えるかは、データ分析の目的によって変わります。
相関分析に限りませんが、データ分析の目的が何かを考えてみましょう。
\[\]
②相関係数が高いからといって、相関があるとは限らない
次の表と散布図を見てください。

これはどう見ても正の相関関係がありますね。
しかし、先ほどやったように層別してみましょう


層別してみると、Aさん、Bさん、Cさん、Dさんのそれぞれの中では相関関係はないと判断できそうです。
つまり、正の相関があると判断したのは、全体的にみて勉強時間とテストの点の間の相関関係でした。
\[\]
それぞれの人においては、勉強時間とテストの点は誤差範囲内の可能性があります。
しかし、全体的にみると勉強時間が増えるするとテストの点が増加するのだから…相関はある!?
(-ω-;)ウーン
やはり、何をデータ分析の目的とするのか、で同じデータであっても現象の捉え方は変わりますね。
\[\]
③相関関係があるからといって、因果関係があるとは限らない
最後に、相関関係と因果関係について説明します。
記事「相関関係1 相関係数とは」にも書いているのですが、復習もかねて解説します。
\[\]
変数Aと変数Bに負の相関関係があったとします。
この時、もし変数Aが原因で変数Bが結果の関係にあるのであれば、変数Aを大きくすると変数Bは小さくなります。
\[\]
しかし、変数Bが原因で変数Aが結果となる場合や、別の要因である変数Cが原因で変数Aや変数Bが結果となる場合はどうでしょうか。
このような場合は、いくら変数Aを大きくしても変数Bは小さくなりません。
(。´・ω・)?
\[\]
抽象的な話でしたので、少し具体例を挙げて考えてみます。
例えば、コンビニのおでんの売り上げとアイスの売り上げを考えましょう。
おでんの売り上げが上がるとアイスの売り上げが下がる「負の相関」があったとします。
\[\]
では、おでんの安売りセールを行えば、アイスの売り上げは下がるのでしょうか?
実験してみないことにはわかりませんが、おそらく影響はないでしょう。
なぜなら、おでんの売り上げとアイスの売り上げには因果関係はないと考えられるためです。
\[\]
因果関係はないのに、相関関係がある。
(-ω-;)ウーン
おでんとアイスの例では、ほかの要因「気温」がこれらの売り上げに影響していると考えられます。
つまり、気温が高い日は、「おでんの売り上げ↓ アイスの売り上げ↑」となり、
気温が低い日は、「おでんの売り上げ↑ アイスの売り上げ↓」となるわけです。
原因が「気温」であるため、おでんの売り上げを上げてもアイスの売り上げが下がるわけではないのです。
また、おでんの売り上げを上げても気温は下がりませんよね。
\[\]
結局、相関関係がわかっても因果関係がわかるわけではないです。
強いて言うなら、「因果関係がある可能性」を見つけられるかも となります。
では、因果関係をどう判断すればよいのか?というと
「なぜなぜ分析」や「連関図法」を使って因果関係を明確にしていくことが重要になります。
\[\]
まとめ
①管理図作成前は、単位・規格値・管理図の意味を確認
②管理限界線を決める時は分布形状も気にしよう
③ありたい姿をイメージして管理図を作ろう
\[\]
今回は管理図について説明しました。
ホントはエクセルを使った(データ分析)t検定の方法を説明したかったのですが、エクセルのバージョン的にできませんでした。
ひとまず、今回はここまでにします。
他の記事も読んでみてください。
\[\]











[…] 前回の記事「【実践 3】相関関係」に引き続き、今回はQC検定実践編として、適合度の検定・分割表について考えていきます。 […]