【実践 1】工程能力指数とヒストグラム
公開日2021年5月2日 最終更新日 2021年6月21日
みなさんこんにちは、michiです。
QC検定も合格して一息ついていると、ほぼ間違いなく言われることがありますよね。
「じゃあ、実践で使ってみて」
資格を持っていることと、知識として使えることは別です。
シリーズ【実践編】では、QC検定で学んだ知識の活用を提案していきます。
QC検定1級の論述対策になる・・・カモ
今回のテーマは「工程能力指数」です。
キーワード:「工程能力指数」「正規分布」
目次
①ヒストグラムの作成
ヒストグラム作成の目的・注意点
いきなり工程能力指数を計算する前に、まずはヒストグラムを作成します。
ヒストグラムを作成する目的は、異常がないデータかを確認するためです。
例えば、ヒストグラム①を見てください。

ヒストグラム①では異常値があるため、工程能力指数は1以下になってしまいます。
しかし、異常値の原因が判明していて、工程が改善されているとします。
そうであるならば、異常値を取り除いて工程能力指数を再計算し、評価し直す必要があります。

\[\]
また、基本的なことですが、そもそも分布は規格値を満たせているのかを確認します。
ヒストグラム②を見てください。

\[\]
工程能力指数\(C_p\) は、計算上1.33以上なので、改善の必要はないと考えられます。
しかし、そもそも規格を満たせていません!
そんな馬鹿な誤判断なんてしないだろう!っと思いますよね?
(ヾノ・∀・`)ナイナイ
\[\]
本当にそうでしょうか?
計算式だけを覚えていて、数値で判断することに固執すると、案外この罠にはまってしまいますよ。
特に工程能力指数\(C_p\) は分布の幅と規格の幅を比較しているにすぎないので、きをつけましょう!
\[\]
②ヒストグラムの作成手順
ヒストグラムは次の手順で作成します。
- データ収集
- データの最大値と最小値を求める
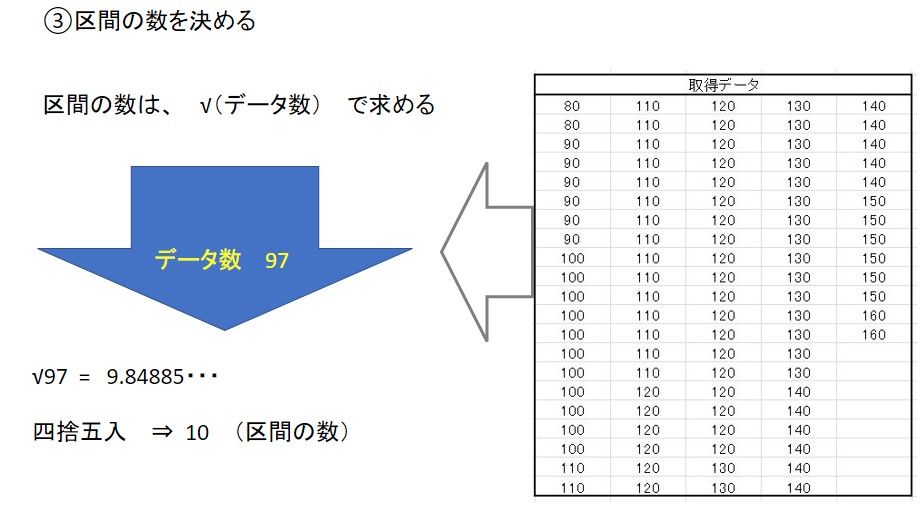
- 区間の数を決める
- 区間の幅を決める
- 区間の境界値を決める
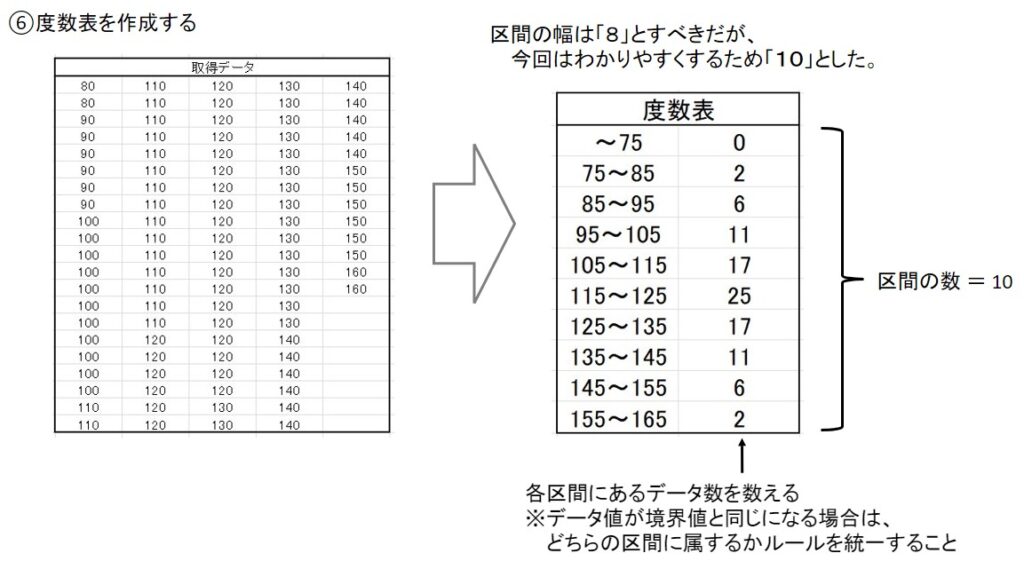
- 度数表を作成する
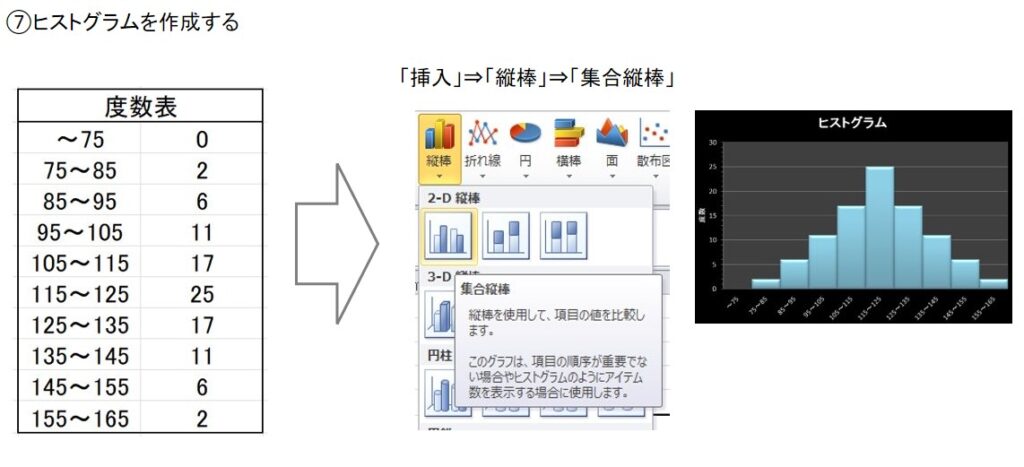
- ヒストグラムを作成する
下に手順を図示したので参考にしてみてください。
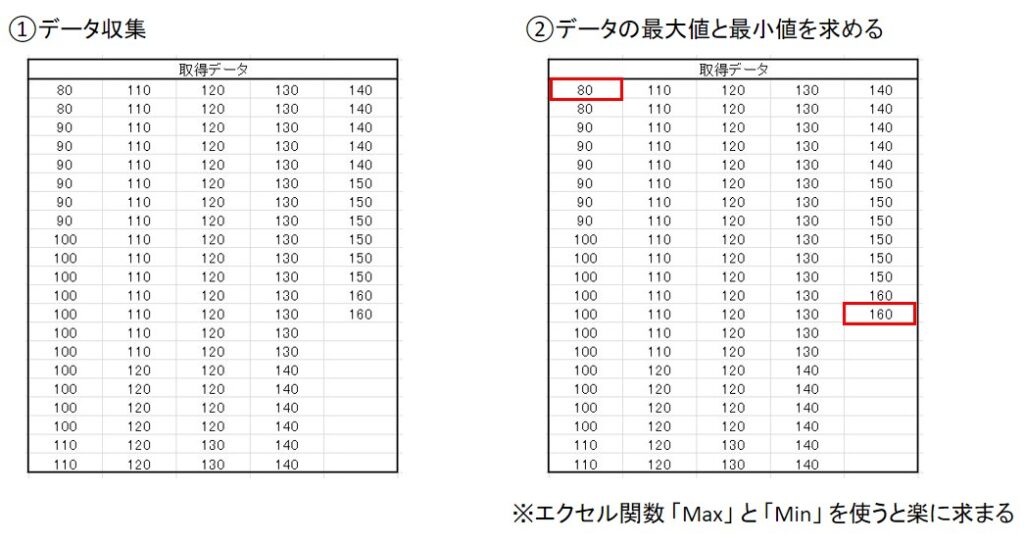
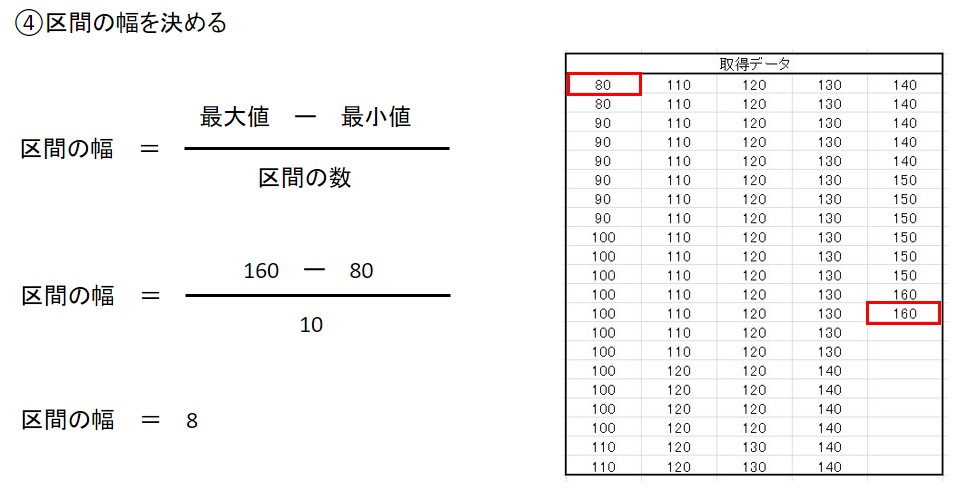
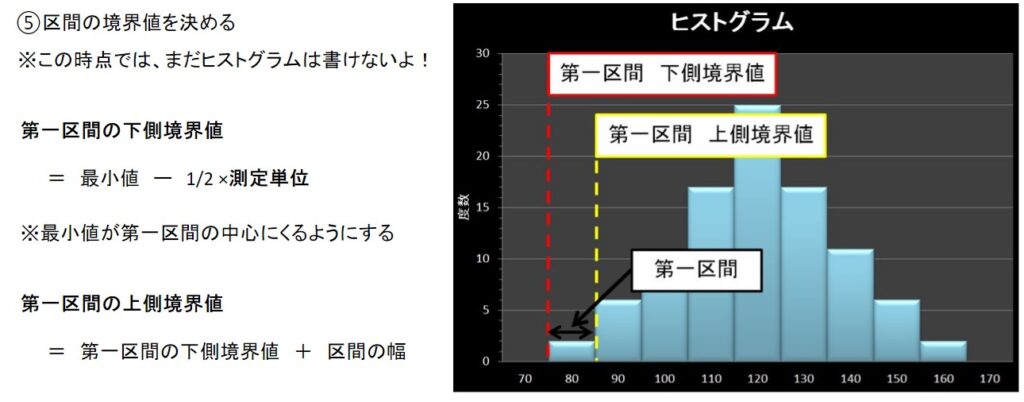
※測定単位とは、測定値の最小単位のことです。
今回の場合は、「1」なので、1/2×測定単位=0.5 となります。
\[\]
ここでのポイントは、区間の数です。
区間の数はルール上は「\(\sqrt{データ数}\)」で求めた値を、整数値になるように四捨五入して求めます。
原則としてはこれでも良いのですが、見やすいデータ収集ができるように、区間の数を変更できるようにしておくと良いでしょう。
\[\]
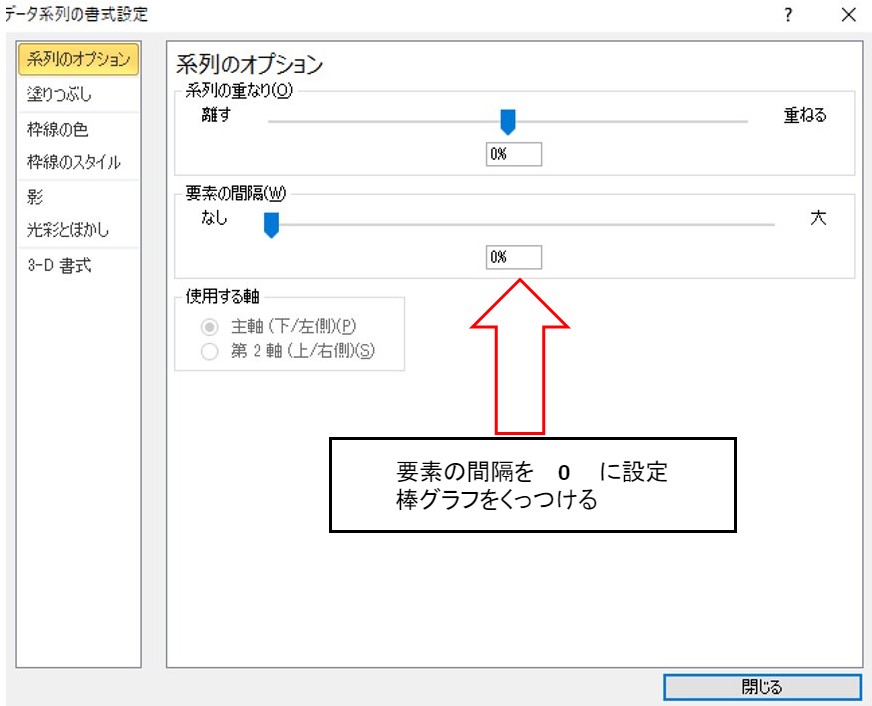
また、棒グラフ同士はくっつけるようにします。
理由はデータは連続的に分布するものというのを表すためのお作法です。
そう、あくまでお作法です。
\[\]
また、ヒストグラムの横軸の範囲を変える場合があります。
- 規格値をヒストグラムに入れる
- 異常値を入れる
- 他のヒストグラムと重ね合わせる
- ・・・
このような場合は、「④区間の幅を決める」で決めた区間の幅を変えるのではなく、横軸の最大値をずらすようにします。

\[\]
②工程能力指数を計算する(正規分布)
さて、ヒストグラムを作成し、分布がヒストグラムっぽいなと判断できたとしましょう。
するとあとは簡単で、平均値と標準偏差を求めて、工程能力指数を計算するだけです。
エクセルの関数を使う際は、平均値は「AVERAGE」を、標準偏差は「STDEV.S」を使うと楽に計算できます。
※「STDEV.S」は標本の標準偏差を求める場合に使います。
母集団として標準偏差を求める場合は「STDEV.P」を使います。
\[\]
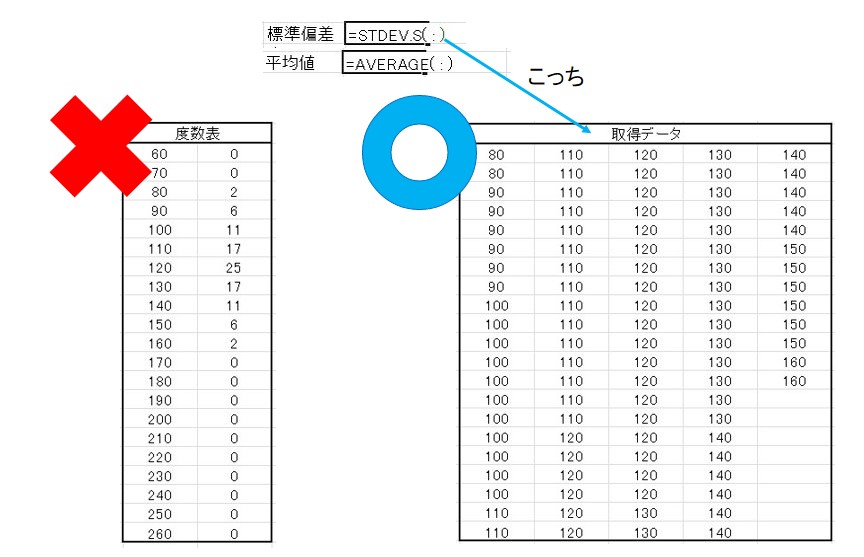
平均値や標準偏差を計算するときに気を付けることは、
「度数表ではなくデータに対して集計を行うこと」 です。
\[\]
③工程能力指数を計算する(非正規分布)
さて、ヒストグラムを作成した時に、データが必ずしも正規分布になるとは限りません。
(個人的には、正規分布になるほうがまれ)
分布がきれいな正規分布にならない時の対処法を提案しますので、参考にしてみてください。
1.ヒストグラムが二山型の場合
ヒストグラムが二山型の場合は簡単です。
データを層別してくだい!
そして、層別したデータ毎に \(C_p\) と\(C_{pk}\) を求めてください。
ただし、データそれ自体を層別(グループ分け)してはいけません。
層別する際は、装置毎・材料毎などの「5M+E」の観点で層別します。
そうすることで、工程能力指数を満足できる場合とできない場合で何がその差を生んでいる原因なのかを推定できるようになります。

\[\]
2.ヒストグラムが絶壁型の場合
ヒストグラムが絶壁型といっても次の3種類が考えられます。
- 分布の頂点がわからない
- 分布の頂点はわかり、分布は左右対称なことがわかっている
- 分布の頂点はわかり、分布は左右非対称なことがわかっている
\[\]
①分布の頂点がわからない
この場合の対処法について考えてみましょう。
ヒストグラムが絶壁型の場合は、「意図して規格以外のものを除去した時に現れる形状」です。
分布の頂点が分からないような絶壁型の場合、「分布は左右対称なのか」、「平均値はどこにあるのか」がわかりません。
一言でいうと「お手上げ」です。
ヽ( ̄ー ̄ )ノ オテアゲー
まずは、規格以外のデータも収集し、全体の分布がわかるようなヒストグラムが作れるようにしましょう。

\[\]
もしデータ収集に時間がかかり、すぐに対応できない場合は、似たような分布を示すデータを基に推測します。
残っているデータ数と全体のデータ数の比から、絶壁型のヒストグラムで見えている部分が全体の〇%と仮定します。
あとは似たような分布を参考に平均値と標準偏差を見積もるわけです。

\[\]
②分布の頂点はわかり、分布は左右対称なことがわかっている
分布が左右対称ということは、「平均値=中央値=最頻値」 が成り立つ状態です。
\[\]
このような場合は、データの平均値(=中央値・最頻値)で折り返すようにして、全体の分布を推測します。

この補正された分布をもとに、標準偏差を計算することで、ヒストグラムが絶壁型であっても、工程能力指数を見積もることができます。
\[\]
③分布の頂点はわかり、分布は左右非対称なことがわかっている
この場合、工程能力指数の計算をそのまま使ってはいけません。
なぜなら、平均値が必ずしもデータをよく表している統計量とは言えないからです。
また、標準偏差も左右非対称であることから、分布の形を反映したばらつきとは言えなくなります。
\[\]
例えば、次のヒストグラムを見てください。

ではどうすればよいのでしょうか?
(。´・ω・)?
\[\]
対処法としては、「最頻値で左右に分け、ヒストグラムを作成する」です。
例えば、先ほどの偏りのあるヒストグラムであれば、最頻値で左右に分けます。
左右それぞれに対し、最頻値=平均値になるように折り返して、正規分布っぽくします。
こうすることで、左側と右側に分けて標準偏差の計算ができるようになります。


\[\]
気をつけるポイントは、\(C_{pk}\)のみを考えることです。
左右それぞれで折り返して作成したヒストグラムは、計算の便宜上折り返して仮定しているため、実際の分布ではありません。
分布に偏りがあることから、\(C_{p}\)を考えるのは不適格と言えるでしょう。
\[\]
④工程能力指数を計算する(指数分布の場合)
さて、今までは二山型や絶壁型もありましたが、基本的に分布は正規分布をを前提としています。
この時の工程能力指数は、正規分布するという前提の下で、99.7%が分布する領域と規格の幅の比を計算することで求めています。
しかし、指数分布の場合は、正規分布のように級を求めてからヒストグラムを作成する方法はうまくいきません。
理由は、級の幅が桁レベルで変わるからです。(下図)
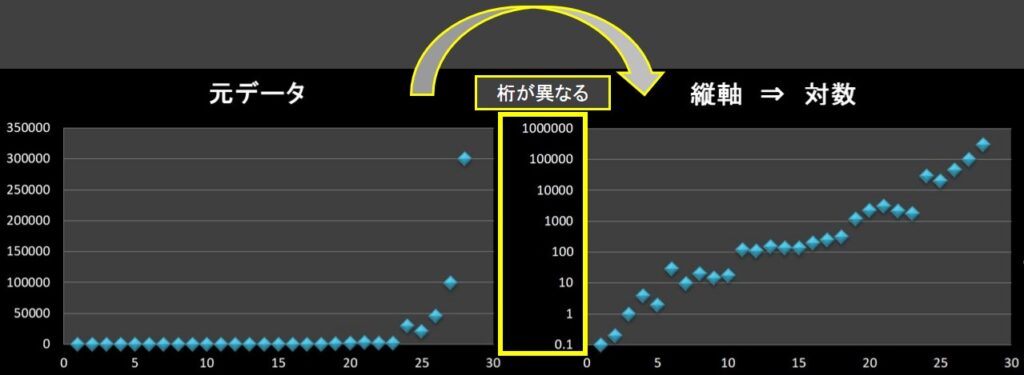
桁レベルで異なるということは、手順通りの方法ではヒストグラムの級の幅を求められないことになります。
(A;´・ω・)アセアセ
\[\]
では、どうすればいいのかと言うと、対数変換をします。
エクセル関数「LN」を使うとできます。
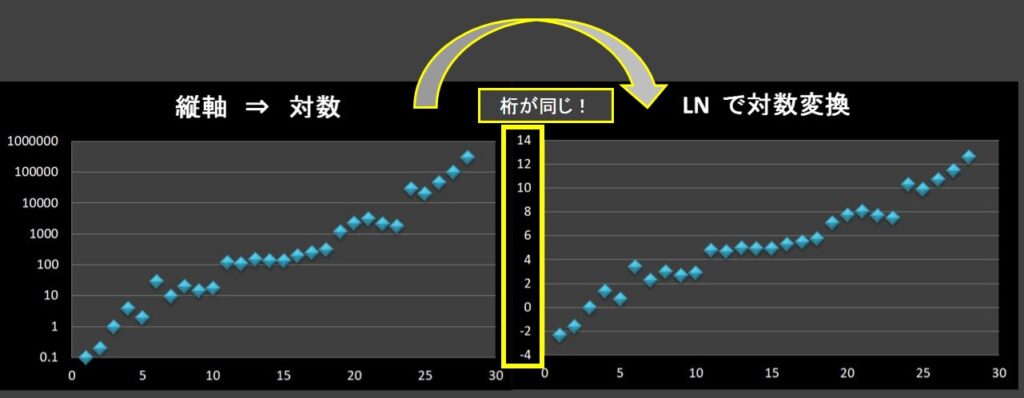
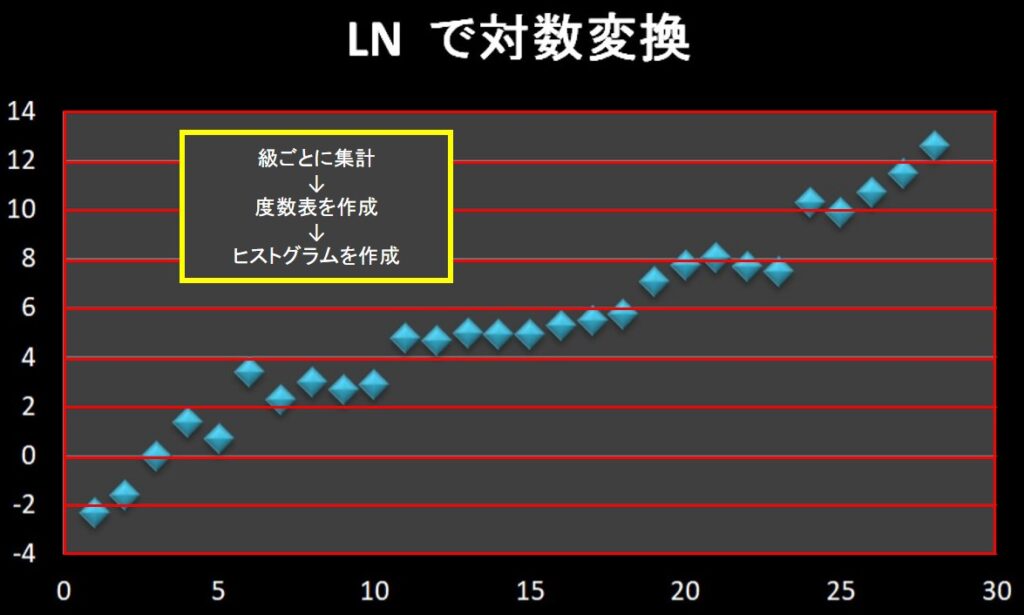
\[\]
対数変換で求めた値に対してヒストグラムを作成し、工程能力指数を計算します。
この時、規格値も対数変換することを忘れないようにしましょう。
\[\]
まとめ
①ヒストグラムの作成は臨機応変に
②工程能力指数はエクセルの関数を使うと楽
③分布が正規分布の形でない時は、層別したり予測したりする
④分布が指数分布の場合は、対数変換を行う
\[\]
工程能力指数もヒストグラムもQC検定3級で出題されます。
3級であれば資格を所有している人も少なくないと思います。
今回の紹介事例を参考に「じゃあ、実践で使ってみて」くださいね
\[\]












[…] 前回の記事「【実践 1】工程能力指数とヒストグラム」に引き続き、今回はQC検定実践編として、管理図について考えていきます。 […]