実験計画法2 二元配置実験

公開日2020年8月15日 最終更新日 2022年3月19日
みなさんこんにちは、michiです。
今回は前回学んだ実験計画法(一元配置実験)の続きで、二元配置実験について学んでいきます。
今回の記事もかなり長めの記事なので、時間がある時にご確認ください。
キーワード:「二元配置実験」「有効反復係数」「田口の公式」
目次
①二元配置実験とは
二元配置実験とは、二つの因子の各水準の組み合わせに対して、ばらつきを評価する方法になります。
一元配置実験では一つの因子に対して、各水準の実験を繰り返し、ばらつきを評価、最も特性上良いものを見つけることを目的にしました。
二元配置実験では、繰り返しのある場合とない場合がありますが、基本的には同じ考えになります。
つまり、水準の中で最も良い特性の「組み合わせ」を見つけることを目的とします。
ここで重要になってくるのは、「組み合わせ」で考えることです。
「組み合わせ」を求める際には、繰り返しがある場合は、「交互作用」を考慮する必要が出てきます。

\[\]
②交互作用とは
交互作用とは、一方の因子がとる水準によって、他方の因子の効果に違いが生じる時、この組み合わせの効果のことを言います。
\[\]
具体例を考えてみましょう。
あなたはスーパーの店員さんで、新商品の「練乳」と「しゃぶしゃぶのたれ」を売りたいと考えています。
どこに配置するのがベストでしょうか?
「練乳」は果物(イチゴ)のそば、「しゃぶしゃぶのたれ」はお肉売り場に置くと良さそうですよね。
\[\]
もし、「しゃぶしゃぶのたれ」を果物(イチゴ)のそば、「練乳」をお肉売り場に置くとどうなるでしょうか?
おそらく売り上げに違いが出そうですよね?
このように、組み合わせが変わると結果が変わることが交互作用のイメージになります。
交互作用がない状態というのは、「練乳」と「しゃぶしゃぶのたれ」をどこに置いても売り上げに影響しない状態になります。
そう考えると、日常生活では交互作用がない場合を考えるほうが難しいかもしれませんね。

\[\]
さて、この交互作用ですが、交互作用の有無を判断するには重要な条件があります。
それは、「繰り返すこと」です。
例えば、先ほどの「練乳」と「しゃぶしゃぶのたれ」の例では、とある一日だけ「練乳」を果物(イチゴ)のそばに置いて売り上げが増加したとします。
しかし一日だけの結果では、その売り上げの増加が「たまたま」なのか「交互作用」によるものなのか、「判断できない」のです。
「練乳」と「しゃぶしゃぶのたれ」の配置をランダムに変える検証を複数回実施することで、「たまたま」ではなく「交互作用」による効果と判断できるようになります。
\[\]
これまで、実例で交互作用のイメージをお伝えしました。
QC検定2級では、一元配置実験と同様に分散分析表を埋めるような問題が出題さます。
交互作用がある場合の分散分析表は下表のとおりです。

一元配置実験の分散分析表と比較すると、「因子B」と「交互作用A×B」の行が追加されています。
この時、自由度に関する以下の関係式は必ず覚えましょう。
\[交互作用A×Bの自由度=因子Aの自由度×因子Bの自由度\]
\[\]
これが、二元配置実験の分散分析表の特徴です。
それでは、例題を解きながら二元配置実験を学んでいきましょう。

\[\]
③実例を解いてみる(交互作用なし)
それでは、早速例題を解いてみましょう。
問)父、母、兄、姉、私が、道具を使ってニャン太君をなでなでしたところ、ニャン太君の滞在時間は下表のようになった。

この時、因子A(人)と因子B(道具)で、水準間で有意な差があるか検定を行い、有意な差がある場合は、信頼度95%で信頼区間を求めよ。
\[\]
問題を解く手順は、前回の記事「実験計画法1 一元配置実験」で紹介した、手順とほぼ同じになります。
- データの二乗表を作る
- 修正項(CT)を求める
- 各平方和(総平方和\(S_T\)、級間平方和\(S_A\)、誤差平方和\(S_E\))を求める
- 各自由度(総自由度\(Φ_T\)、因子Aの自由度\(Φ_A\)、因子Bの自由度\(Φ_B\)、誤差の自由度\(Φ_E\))を求める
- 各不偏分散と分散比を求める
- 分散分析表を作る
- F検定を行う
- 各水準の母平均の点推定を行う
- 信頼区間の幅を求める
- 最適条件を選ぶ
それでは、解いていきましょう
\[\]
①データの二乗表を作る
問題文で与えられた表の数値を二乗して、二乗表を作成します。

\[\]
②修正項(CT)を求める
次の計算式より修正項を求めます。
\[CT=\frac{(データの合計)^2}{データ数} \qquad =\frac{68^2}{20}\qquad=231.2 \]
\[\]
③各平方和(総平方和\(S_T\)、級間平方和\(S_A\)、級間平方和\(S_B\)、誤差平方和\(S_E\))を求める
各平方和を求めていきます。
まずは総平方和\(S_T\)は
\[総平方和S_T=\sum(データの二乗)−修正項(CT)=344−231.2=112.8\]
次に級間平方和\(S_A\)は
\[級間平方和S_A=\sum_{i=1}^5 \frac{(A_iの合計)^2}{A_iのデータ数}\qquad–修正項(CT)\]
\[S_A=\frac{13×13}{4}+\frac{12×12}{4}+\frac{8×8}{4}+\frac{9×9}{4}+\frac{26×26}{4}-231.2=52.3\]
※因子Aは人による因子でした、人は5人いるので5水準になります。同じ人に対し、道具は4種類あるので、分母は4になります。
同様に級間平方和\(S_B\)は
\[級間平方和S_B=\sum_{i=1}^4 \frac{(B_iの合計)^2}{B_iのデータ数}\qquad–修正項(CT)\]
\[S_B=\frac{28×28}{5}+\frac{15×15}{5}+\frac{17×17}{5}+\frac{8×8}{5}-231.2=41.2\]
※因子Bは道具による因子でした、道具は4種類あるので4水準になります。同じ道具に対し、人は5人いるので、分母は5になります。
\[\]
交互作用はない場合を考えているので、誤差平方和を求めます。
誤差平方和\(S_E\) は、
\[誤差平方和S_E=総平方和S_T−級間平方和S_A−級間平方和S_B\]
\[S_E=112.8-52.3-41.2=19.3\]
\[\]
④各自由度(総自由度\(Φ_T\)、因子Aの自由度\(Φ_A\)、因子Bの自由度\(Φ_B\)、誤差の自由度\(Φ_E\))を求める
各自由度を計算すると、下記の通りになります。
- 全体の自由度\(Φ_T=総データ数-1=20-1=19\)
- 因子Aの自由度\(Φ_A=水準数-1=5-1=4\)
- 因子Bの自由度\(Φ_B=水準数-1=4-1=3\)
- 誤差の自由度\(Φ_E=Φ_T-Φ_A-Φ_B=19-4-3=12\)
\[\]
⑤各不偏分散と分散比を求める
分散比\(F_0\) は、因子Aに対するものと、因子Bに対するものがあります。
計算すると下のようになります。
\[V_A=\frac{S_A}{Φ_A}=\frac{52.3}{4}=13.075\]
\[V_B=\frac{S_B}{Φ_B}=\frac{41.2}{3}=13.73\]
\[V_E=\frac{S_E}{Φ_E}=\frac{19.3}{12}=1.608\]
\[A:F_0=\frac{V_A}{V_E}=\frac{13.075}{1.608}=8.131\]
\[B:F_0=\frac{V_B}{V_E}=\frac{13.733}{1.608}=8.540\]
\[\]
⑥分散分析表を作る
⑤までで求めた数値を分散分析表に展開すると、下表の結果になります。

\[\]
⑦F検定を行う
分散分析の結果に対してF検定を実施します。
今回は、因子Aと因子Bの二つの因子に対して行います。
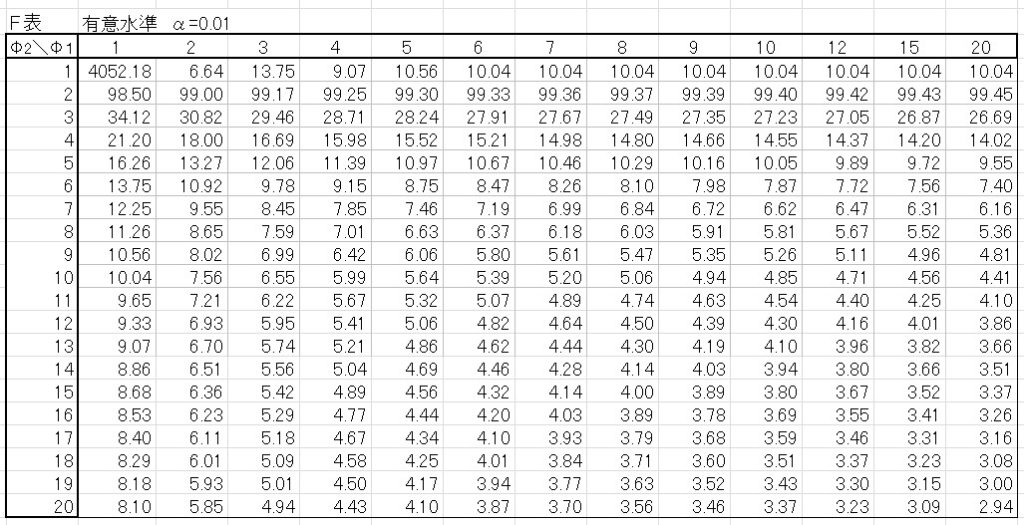
F表は下の表になります。

(;´・д・)=3ハァ ミルノシンド
F表の値は、F(因子A or Bの自由度、誤差の自由度:\(α\))で表されます。
結果は下のようになります。
- 因子AのF表の値 F(4,12:0.05)=3.26
- 因子AのF表の値 F(4,12:0.01)=5.41
- 因子BのF表の値 F(3,12:0.05)=3.49
- 因子BのF表の値 F(3,12:0.01)=5.95
よって、「因子A、因子Bの分散比 > F表の値」なので、「因子A、因子Bの水準間に(高度に)有意な差がみられる」と判定します。
「高度に」とつく理由は、\(α=0.01\) の時のF表の値よりも分散比が大きいためです。
以上の検定結果から、水準間に有意な差が見られるので、推定を行います。
\[\]
⑧各水準の母平均の点推定を行う
一元配置実験の時と同じで、「母平均(\(μ\))=各水準の平均値」となります。
問題文の値(下表)より、

因子Aの母平均は、
- \(A_父\)水準の母平均\(=\frac{13}{4}=3.25\)
- \(A_母\)水準の母平均\(=\frac{12}{4}=3.00\)
- \(A_兄\)水準の母平均\(=\frac{8}{4}=2.00\)
- \(A_姉\)水準の母平均\(=\frac{9}{4}=2.25\)
- \(A_私\)水準の母平均\(=\frac{26}{4}=6.50\)
因子Bの母平均は、
- \(B_{ねこじゃすり}\)水準の母平均\(=\frac{28}{5}=5.60\)
- \(B_{素手}\)水準の母平均\(=\frac{15}{5}=3.00\)
- \(B_{道具①}\)水準の母平均\(=\frac{17}{5}=3.40\)
- \(B_{道具②}\)水準の母平均\(=\frac{8}{5}=1.60\)
\[\]
⑨信頼区間の幅を求める
信頼区間の幅は、\(水準の平均±t(Φ_E,0.05)×\sqrt{\frac{V_E}{n_i}}\) で求められます。
※\(n_i\) :各水準ごとの観測数
誤差の自由度\(Φ_E\) と不信頼度からt表の値を読み取ると、
\[t(12,0.05)=2.179\]
誤差の不偏分散\(V_e=1.608\) ,因子Aの水準毎の観測数\(n_i=4\) , 因子Bの水準毎の観測数\(n_i=5\) なので
因子Aの区間の幅は、
\[t(12,0.05)×\sqrt{\frac{1.608}{4}}≒1.382\]
因子Bの区間の幅は、
\[t(12,0.05)×\sqrt{\frac{1.608}{5}}≒1.236\]
以上より、各水準の母平均の区間推定を実施すると、下のようになります。
因子Aの母平均は、
- 1.868< \(A_父\)水準の母平均 < 4.632
- 1.618 < \(A_母\)水準の母平均 < 4.382
- 0.618 < \(A_兄\)水準の母平均 < 3.382
- 0.868 < \(A_姉\)水準の母平均 < 3.632
- 5.118 < \(A_私\)水準の母平均 < 7.882
因子Bの母平均は、
- 4.364 < \(B_{ねこじゃすり}\)水準の母平均 < 6.836
- 1.764 < \(B_{素手}\)水準の母平均 < 4.236
- 2.164 < \(B_{道具①}\)水準の母平均 < 4.636
- 0.364 < \(B_{道具②}\)水準の母平均 < 2.836
この関係を図示すると、下図のようになります。

※数値は図が見にくくなるので省略しています。
\[\]
⑩最適条件を選ぶ
前回の記事「実験計画法1 一元配置実験」では、「水準間の差を検定する」と書きました。
一元配置実験では水準間の差が有意かを判定し、最適条件の妥当性を考えました。
本質的には同じで、どの水準の組み合わせがベストな「組み合わせ」なのかを選びます。
といってもそんなに難しく考える必要はなく、区間推定で作成した表を見れば、一目瞭然となります。
因子Aは私で、因子Bはねこじゃすりがベストな組み合わせになりそうです。
\[\]
⑪最適条件の母平均を推定する
最適条件の点推定は以下の式で計算します。
\[因子Aの最適条件の平均値+因子Bの最適条件の平均値-総平均値\]
今回の問題では、最適条件は因子Aが私、因子Bがねこじゃすりなので、
\[A_私の平均値+B_{ねこじゃすり}の平均値-総平均 = \frac{26}{4}+\frac{28}{5}-\frac{68}{20}=8.7\]
\[\]
なぜ、総平均値を引き算するのかというと、二つの水準の平均を足しているため、総平均値の分だけ大きくなっているためです。
もう少しわかりやすくするため、簡単な例を考えてみます。(下図)

最適条件(一番良い結果)は「Aさん、国語」ですが、Aさんという水準(赤枠)と国語という水準(青枠)が重なっています。
このまま平均値同士を足し算すると、枠が重なっている分だけ点推定の値を多く見積もってしまいます。
ですので、「枠の重なっている分=総平均値」を引き算します。
\[\]
確かに、平均値の和は150(Aさん、国語)で、そこから50(総平均)を引き算すると、表の値になります。
\[\]
次に信頼度95%で信頼区間を求めるのですが、次式で計算します。
\[μ±t(Φ_E,0.05)×\sqrt{\frac{V_E}{n_E}}\]
ここで、\(n_E\) は有効反復係数といい、次の式で表されます。
\[n_E=\frac{abn}{1+Φ_A+Φ_B+Φ_{A×B}}\]
\[a:Aの水準数, b:Bの水準数, n:繰り返しの数\]
\[Φ_A:Aの自由度, Φ_B:Bの自由度, Φ_{A×B}:交互作用の自由度\]
この式を「田口の公式」といいます。
※有効反復係数の詳細は、この記事の最後に書きます。
今回の例題では、繰り返しのない場合(交互作用がない場合)なので、先ほどの田口の公式は以下のようになります。
\[n_E=\frac{ab}{1+Φ_A+Φ_B}=\frac{5×4}{1+3+4}=2.5\]
よって、信頼区間の幅は、
\[t(Φ_E,0.05)×\sqrt{\frac{V_E}{n_E}}=2.179×\sqrt{\frac{1.608}{2.5}}=1.748\]
以上より、最適条件\(A_私B_{ねこじゃすり}\) の信頼度95%母平均区間は、\(6.95~10.45\) となります。
\[\]
結構大変に思いますが、やることはワンパターンなので、繰り返し練習をして覚えましょう。

\[\]
④実例を解いてみる(交互作用あり)
それでは、今度は繰り返しのある二元配置実験について解いてみましょう。
問)父、母、兄、姉、私が、道具を使ってニャン太君をなでなでしたところ、ニャン太君の滞在時間は下表のようになった。

この時、因子A(人)と因子B(道具)で、水準間で有意差な差があるか検定を行い、有意差な差がある場合は、信頼度95%で信頼区間を求めよ。
ただし、\(\sum{(各数値の二乗)}=767\) となる
\[\]
⓪繰り返しのデータを足して、AB二元表を作成
繰り返しのあるデータの場合は、同じ条件の値を足し、AB二元表を作成します。
※AB二元表とは、同じ条件の結果を足し合わせて作る表のこと
すると、問題で与えられたデータは下のAB二元表になります。

\[\]
①データの二乗表を作る
今回の問題のデータの二乗表は下のようになります。

※AB二元表の二乗表ではありません!
※QC検定本番では、表が与えられているか、「\(\sum{(各数値の二乗)}\)」というヒントが問題文中にあります。
ただし、「(\(\sum{各数値}\)) の二乗」と混同しないように気をつけましょう!
\[\]
②修正項\(CT\) を求める
修正項\(CT\) は以下の式で求まります。
\[CT=\frac{(データの合計)^2}{データの数}\qquad=\frac{141×141}{40}=497.025\]
この時注意するのは、母数の「データの数」です。
因子Aは5水準、因子Bは4水準ですが、繰り返し実験をしている(2回)ため、「データ数=40」となります。
\[\]
⑤各平方和を求める
まず総平方和\(S_T\) ですが、問題文にヒント「\(\sum{(各数値の二乗)}=767\)」があるので、
\[S_T=\sum(各数値の二乗)-CT=767-497.025=269.975\]
次に級間平方和\(S_A\)は、AB二元表より、
\[級間平方和S_A=\sum_{i=1}^5 \frac{(A_iの合計)^2}{A_iのデータ数}\qquad–修正項(CT)\]
\[S_A=\frac{24×24}{8}+\frac{28×28}{8}+\frac{16×16}{8}+\frac{17×17}{8}+\frac{56×56}{8}-497.025=133.1\]
\[級間平方和S_B=\sum_{i=1}^4 \frac{(B_iの合計)^2}{B_iのデータ数}\qquad–修正項(CT)\]
\[S_B=\frac{57×57}{10}+\frac{30×30}{10}+\frac{35×35}{10}+\frac{19×19}{10}-497.025=76.475\]
級間平方和\(S_A\)は、各因子に対し、4パターンの因子Bの組み合わせがあり、2回繰り返しているため、分母は「4×2=8」になります。
級間平方和\(S_B\)は、各因子に対し、5パターンの因子Aの組み合わせがあり、2回繰り返しているため、分母は「5×2=10」になります。
次にAB級間平方和\(S_{AB}\) を求めると、
AB二元表のデータの二乗は、下表より

\[級間平方和S_{AB}=\sum \frac{(AB二元表のデータ)^2}{繰り返し数}\qquad–修正項(CT)\]
\[S_{AB}=\frac{1505}{2}-497.025=255.475\]
交互作用\(S_{A×B}\) は、\(S_{AB}=S_A+S_B+S_{A×B}\) という関係式より、
\[交互作用平方和S_{A×B}=S_{AB}-S_A-S_B=255.475-133.1-76.475=45.9\]
よって、誤差の平方和は、
\[S_E=S_T-S_{AB}=S_T-S_A-S_B-S_{A×B}\]
\[S_E=269.975-133.1-76.475-45.9=14.5\]
平方和がいっぱい出てきて混乱しそうです。
下に各平方和の関係のイメージ図を描きます。

\[\]
④各自由度(総自由度\(Φ_T\)、因子Aの自由度\(Φ_A\)、因子Bの自由度\(Φ_B\)、交互作用の自由度\(Φ_{A×B}\)、誤差の自由度\(Φ_E\))を求める
各自由度を計算すると、下記の通りになります。
- 全体の自由度\(Φ_T=総データ数-1=40-1=39\)
- 因子Aの自由度\(Φ_A=水準数-1=5-1=4\)
- 因子Bの自由度\(Φ_B=水準数-1=4-1=3\)
- 交互作用の自由度\(Φ_{A×B}=Φ_A×Φ_B=4×3=12\)
- 誤差の自由度\(Φ_E=Φ_T-Φ_A-Φ_B-Φ_{A×B}=39-4-3-12=20\)
自由度は因子の数で決まるもので、繰り返しの数と関係がないことに気をつけましょう!
\[\]
⑤各不偏分散と分散比を求める
分散比\(F_0\) は、因子Aに対するものと、因子Bに対するもの、さらに交互作用(A×B)に対するものがあります。
計算すると下のようになります。
\[V_A=\frac{S_A}{Φ_A}=\frac{133.1}{4}=33.275\]
\[V_B=\frac{S_B}{Φ_B}=\frac{76.475}{3}=25.491\]
\[V_{A×B}=\frac{S_{A×B}}{Φ_{A×B}}=\frac{45.9}{12}=3.825\]
\[V_E=\frac{S_E}{Φ_E}=\frac{14.5}{20}=0.725\]
よって、各分散比は、
\[A:F_0=\frac{V_A}{V_E}=\frac{33.275}{0.725}≒45.9\]
\[B:F_0=\frac{V_B}{V_E}=\frac{25.491}{0.725}≒35.16\]
\[A×B:F_0=\frac{V_{A×B}}{V_E}=\frac{3.825}{0.725}≒5.28\]
\[\]
⑥分散分析表を作る
⑤までで求めた数値を分散分析表に展開すると、下表の結果になります。

\[\]
⑦F検定を行う
分散分析の結果に対してF検定を実施します。
今回は、因子Aと因子Bの二つの因子に対して行います。
分散分析の結果は、因子Aが45.9、因子Bが35.16、交互作用A×Bが5.28でした。
F表は下の表になります。


(;´・д・)=3ハァ ミルノシンド
F表の値は、F(因子A or B or A×Bの自由度、誤差の自由度:\(α\))で表されます。
結果は下のようになります。
- 因子AのF表の値 F(4,20:0.05)=2.87
- 因子AのF表の値 F(4,20:0.01)=4.43
- 因子BのF表の値 F(3,20:0.05)=3.10
- 因子BのF表の値 F(3,20:0.01)=4.94
- 交互作用A×BのF表の値 F(12,20:0.05)=2.28
- 交互作用A×BのF表の値 F(12,20:0.01)=3.30
よって、「因子A、因子B、交互作用A×Bの分散比 > F表の値」なので、「因子A、因子Bの水準間、交互作用A×Bに(高度に)有意な差がみられる」と判定します。
「高度に」とつく理由は、\(α=0.01\) の時のF表の値よりも分散比が大きいためです。
以上の検定結果から、水準間に有意な差が見られるので、推定を行います。
\[\]
⑧各水準の母平均の点推定を行う
分散分析の結果より、母平均の点推定を行います。
先ほどの例題と同様に、各水準毎の母平均を求め計算するのですが、あまり意味がありません。
Σ(・ω・ノ)ノ!
なぜあまり意味がないかというと、交互作用A×Bが有意になっている(交互作用A×Bがある)と判定されているためです。
交互作用A×Bがない場合の問題では、因子A、因子Bのそれぞれの因子でベストな条件同士を単純に選べばよかったです。
しかし、交互作用A×Bがある場合は、ベスト条件同士の組み合わせが、必ずしも一番効果があるとは言えないためです。
実際、QC検定2級の過去問を見ると、交互作用のある問題は、水準それぞれの推定をする問題は出てこないようです。
\[\]
⑨信頼区間の幅を求める
点推定の場合と同様に、区間の幅も各水準で求める意味はあまりありません。
ベストな組み合わせで信頼度95%の区間推定を有効反復係数を用いて計算するためです。
\[\]
⑩最適条件を選ぶ
では、交互作用A×Bがある場合、どのように最適条件を選べばよいのでしょうか?
答えは簡単で、同一条件の数値を足して(AB二元表の値)、合計の一番高い水準の組み合わせを選択すればよいです。

上表より、「\(A_私B_{ねこじゃすり}\)」がベストな組み合わせということが分かります。
\[\]
⑪最適条件の母平均を推定する
ベストな組み合わせが分かったので、母平均の推定を行います。
\[μ_{ベスト条件}=A_私B_{ねこじゃすり}の平均値=\frac{11+13}{2}=12\]
繰り返し回数が2回のため、信頼度95%の信頼区間の幅は、
\[\bar{μ}±t(Φ_E,0.05)×\sqrt{\frac{V_E}{n_E}}\]
この時、有効反復係数\(n_E\)は、下の計算式より
\[n_E=\frac{abn}{1+Φ_A+Φ_B+Φ_{A×B}}\]
\[a:Aの水準数, b:Bの水準数, n:繰り返しの数\]
\[n_E=\frac{5×4×2}{1+4+3+12}=2\]
よって、
\[\bar{μ}±t(20,0.05)×\sqrt{\frac{0.725}{2}}\]
\[=\bar{μ}±2.086×0.602(≒1.256)\]
したがって、\(μ_{ベスト条件}=12\) なので、最適条件の母平均の区間推定は、
\[10.744 \leq A_私B_{ねこじゃすり} \leq 13.256\]
となります。
私がねこじゃすりを使えば、ニャン太君を10分以上キープできる確率が95%以上ありますが、それでも14分以上キープするのは難しいようです。
\[\]
交互作用がない場合と区間の幅が異なっています。
③の実例では、「交互作用がない」としたため、本来考慮されるべき交互作用分が誤差として換算されていたためです。
\[\]
⑤有効反復係数とは
さて、実例の問題がかなり長かったですね。
例題では有効反復係数\(n_E\) なるものが登場しました。
一元配置実験では各水準ごとの観測数で計算できていたのに、二元配置実験ではこのわけわかんない係数(=有効反復係数)を使わなくてはいけません。
では、なぜ、有効反復係数を使わなければいけないのでしょうか?
(。´・ω・)?
\[\]
区間推定ではt分布を使用します。
t分布はサンプル数(一元配置実験では水準毎の観測数)が増えるごとに、精度があがる(t分布の幅が狭まる)ものでした。
その際に使う「有効なサンプル数を定義しよう」ということをしています。
まだ全然わかりませんよね。
次の3ステップで考えましょう
- 1)一元配置実験の場合
- 2)交互作用のない二元配置実験の場合
- 3)交互作用のある二元配置実験の場合
\[\]
1)一元配置実験の場合
誤差の不偏分散を水準毎の観測数で割り算しました。
区間の幅は平均値に対して、下式で表されます。
\[\bar{μ}±t(Φ_E,0.05)×±\sqrt{\frac{V_E}{n_i}}\]
平方根の中身は、「誤差の不偏分散\(V_E\) を1観測数(データ数)あたりの値に変換」しているとイメージできます。

\[\]
2)交互作用のない二元配置実験の場合
交互作用のない場合は、区間の幅は以下の式で表されます。
\[\bar{μ}±t(Φ_E,0.05)×\sqrt{\frac{V_E}{n_E}}\]
\[\bar{μ}±t(Φ_E,0.05)×\sqrt{V_E×\frac{1}{ab}×(1+Φ_A+Φ_B)}\]
平方根の中身は、
\[\frac{V_E}{n_E}=V_E×\frac{1}{ab}×(1+Φ_A+Φ_B)\]
この数式の意味は、誤差の不偏分散\(V_E\) を全データ数\((=a×b)\) で割り算し、1データ数あたりの誤差の不偏分散を計算します。
その後、最適条件に関するデータ数分\((1+Φ_A+Φ_B)\) を計算しています。

この時注目する点は、「\((1+Φ_A+Φ_B)\)」は、「1+因子の自由度の和」になっていることです。
なんか当たり前のことを言っているような気もしますが、これが重要になります。
\[\]
3))交互作用のある二元配置実験の場合
交互作用のある二元配置実験の場合、有効反復係数は下式(田口の公式)の通りでした。
\[n_E=\frac{abn}{1+Φ_A+Φ_B+Φ_{A×B}}\]
\[a:Aの水準数, b:Bの水準数, n:繰り返しの数\]
交互作用のない二元配置実験と同様に、区間の幅は以下の式で表されます。
\[\bar{μ}±t(Φ_E,0.05)×\sqrt{\frac{V_E}{n_E}}\]
ただし、今回は有効反復係数の形が異なるので、
\[\bar{μ}±t(Φ_E,0.05)×\sqrt{V_E×\frac{1}{abn}×(1+Φ_A+Φ_B+Φ_{A×B})}\]
となります。
先ほどと同様に、平方根の中身を考えてみましょう。
\[\frac{V_E}{n_E}=V_E×\frac{1}{abn}×(1+Φ_A+Φ_B+Φ_{A×B})\]
この式は、誤差の不偏分散\(V_E\) を全データ数\((=a×b×n)\) で1データ数当たりの誤差の不偏分散を計算します。
その後、「1+因子の自由度の和」分の不偏分散を計算します。
交互作用のない場合と比較して、繰り返し回数分と交互作用分を考慮する必要があります。
この時のイメージは下図のようになります。


( ;∀;)
うーん、やっぱり反復係数は少し難しいですよね。
まぁでも有効反復係数が分からなくても、ほかの問題が解ければQC検定2級は合格するので、気楽にいきましょう。
(‘ω’)ノ (元も子もない話を・・・)
まとめ
①組み合わせを考えるときは、「交互作用」も考える
②交互作用A×Bの自由度=因子Aの自由度×因子Bの自由度
③実例はワンパターンで解ける
④田口の公式は覚えづらい
⑤有効反復係数は、イメージすればまぁなんとか覚えられるかなぁ
\[\]
今回は二元配置実験について勉強しました。
書きたいが多く、更新も遅れてしまいました。
次回からは週一回のペースで新しい記事を更新していきます。
次回は「サンプリング」について学んでいきましょう。
\[\]













[…] このブログでも「実験計画法」は一番読まれている記事です。 […]
[…] 前回の記事では二元配置実験について学びました。 […]
michiさん、
QC2級目指して勉強中ですが、実験計画の交互作用ありが中々理解できずもやもやとしていましたが、とてもスッキリしました。感激です。繰り返しありのnEの式のbとφBの値が-1されているように思いました。
コメントありがとうございます。
修正しました。(21.07.27)
QC検定2級合格のお手伝いができれば幸いです。
はじめまして。
こちらのサイトの説明が参考書よりずっとわかりやすく、2級の勉強にめちゃくちゃ活用させていただいております。ありがとうございます!!
(交互作用ありの最適条件の母平均の区間推定にて、有効反復係数を求める式中a,bの値が自由度になっているような気がします)。
はじめまして。
当サイトをお褒めいただき嬉しい限りです。
また、当サイトがお役立ちできたようで幸いです。
交互作用のご指摘ありがとうございます。
修正しました。
明日はQC検定の試験日ですね。
もし受検されるのであれば、合格するようご武運をお祈りします!
きっと大丈夫です!
[…] 実験計画法で計算した時と同様に、因子A及びその交互作用を計算します。 […]
すみません、
μベスト条件=私ねこじゃすりの平均値=(11+13)/2=12
の11と13がどこから来たのか分からず……まったくの統計初心者なのですが良ければお教え下さい。
ご愛読ありがとうございます。
μベスト条件の 11 と 13 は、「ニャン太君滞在時間」の「私」が「ねこじゃすり」を使ったときの結果です。
④実例を解いてみる(交互作用あり) の最初の方に対応表があります。
その平均をとって、12としています。
引き続き当ブログをご愛顧賜りますようよろしくお願いいたします。