実験計画法１　一元配置実験

公開日2020年7月28日 　最終更新日 2021年9月19日

みなさんこんにちは、michiです。

前回の記事では回帰分析の手順を学びました。

今回は実験計画法について勉強していきます。

今回はちょっと長めの記事になります。

①実験計画法とは

実験計画法の目的は、少ない検証数で一番良い水準を見極めることです。

例えば次の場合を考えてみましょう。

例）猫さんが満足できるようになでなでしたい。次の３種類の因子がある

• 父がなでなで or 母がなでなで
• 「ねこじゃすり」でなでなで　or　素手でなでなで
• 雨の日になでなで or 晴れの日になでなで

現実的に猫さんに満足度を聞くことはできませんが、何回検証実験が必要でしょうか？

普通に考えたら、2×2×2=8回 必要ですよね。

しかし、実験計画法では4回でよいのです。

実験計画法における組み合わせは下表のようになります。。

このように、因子が3つ以上ある実験を多元配置実験というのですが、QC検定2級では出題されません。

ヾ(・＿・；） オイオイ

QC検定2級で出題されるのは、因子が1つの一元配置実験か、因子が2つの二元配置実験になります。

多元配置実験を学ぶわけではないので、実用性でいうと物足りない感も否めませんが、実験計画法を学ぶために、一元配置実験と二元配置実験を学んでいきましょう。

\[\]

本題に入る前に、次の専門用語を覚えておきましょう。

• 因子：検証で比較したい条件
• 水準：各因子の持つ条件

先ほどの猫さんの例で考えると、「誰が、何で、どんな天気の日に」の３つの因子があることが分かります。

この時、三つの因子それぞれに、２つずつの水準があることも分かります。

\[\]

また、因子には次の３種類があります。

• 制御因子：水準の指定や選択が可能なもの
• 標示因子：実験では制御するが、適用の場では制御できるとは限らないもの
• 誤差因子：実験結果がばらつく要因で、制御できないもの

先ほどの猫さんの例でまた考えると、「誰が、何で」は制御因子で、「どんな天気の日に」は標示因子になります。

天気は実験では選択できても、天気自体を常にコントロールはできませんよね。

誤差因子は、例えば「ねこじゃすり」の出来栄えや父母の体調など、因子がばらつく要因となるものです。

\[\]

②フィッシャーの三原則とは

フィッシャーの三原則は次の三つです。

• 反復の原則：繰り返し実験を行うことで、精度を上げる
• 無作為の原則：実験の慣れ（系統誤差）を偶然誤差にするため、ランダムに実験する
• 局所管理の原則：系統誤差の発生する要因毎に「ブロック」にわけ、ブロック内に比較したい条件を入れる

「①実験計画法とは」で例に挙げた、猫さんをなでなでする場合で考えてみましょう。

・反復の原則は、イメージしやすいと思います。

実験を１回やって終了するのではなく、何度か繰り返すことで、水準間の違いをはっきりさせます。

\[\]

・無作為の原則は、父と母が規則的に交互に猫さんをなでなでした場合、母のなでなでに満足したのか、父の次に母がなでなですることで満足したのか、わかりません。

このように順番によって生まれる「系統誤差」をなくすため、くじ引きなどで実験をする順番をランダムにします。

\[\]

・局所管理の原則は、ほかの要因が猫さんの満足度に影響しないようにすることです。

例えば、先ほどの例では取り上げなかった、なでなでのタイミング（時間）やソファーの上（場所）など、ほかの因子を揃えて実験します。

以上がフィッシャーの三原則になります。

\[\]

③分散分析法の考え方（一元配置法の場合）

回帰分析で使用したように、実験計画法でも分散分析表を使います。

回帰分析では、「回帰による変動が、残差による変動より、全体に与える影響が大きいか」を検定しました。

一元配置法における分散分析は、因子の水準を変えたことで「級間変動が、級内変動より、全体に与える影響が大きいか」を検定します。

さてNewワードが出てきました。次の意味です。

• 級間変動：因子の水準の違いよる変動（=級間平方和\(S_A\)）
• 級内変動：因子以外の要因による変動（=誤算平方和\(S_E\)）

級間平方和\(S_A\) の求め方は、次の章で手順を説明します。

回帰分析と同様に分散分析表を作成すると、下図のようになります。

この時 \(F_0 = \frac{V_A}{V_E} > F(Φ_A,Φ_E;α)\) であれば、有意差ありと判定されます。

意味としては、「因子の水準間に有意な差がみられる」と判定しています。

F検定を行うのは、回帰分析の時と同じ理由で、ばらつき具合を比較評価するためです。

※回帰分析では、回帰による自由度は常に「１」でしたが、実験計画法では各因子の自由度は、「水準の数-1」となります。

全体の自由度は「データ数-1」となり、誤算の自由度は、「全体の自由度ー因子のの自由度＝データ数ー水準の数」となります。

\[\]

④分散分析の手順

それでは、実験計画法における分散分析の手順を紹介します。

1. データの二乗表を作る
2. 修正項（CT）を求める
3. 各平方和（総平方和\(S_T\)、級間平方和\(S_A\)、級内平方和\(S_E\)）を求める
4. 各自由度（総自由度\(Φ_T\)、因子Aの自由度\(Φ_A\)、誤差の自由度\(Φ_E\)）を求める
5. 各不偏分散と分散比を求める
6. 分散分析表を作る
7. F検定を行う
8. 各水準の母平均の点推定を行う
9. 信頼区間の幅を求める
10. 水準間の差を検定する

(⌒(´-ω-)_　長いよ

\[\]

よく見ると、③～⑦は回帰分析と同じようなやり方をしています。

①、②は分析を始めるための事前準備みたいなものです。

⑧～⑩が実験計画法における推定になります。

では、簡単に、それぞれやっていることを説明します。

\[\]

①データの二乗表を作る

実験計画法の問題では、測定データのみを与えられている場合がほどんどで、自分で平方和（ばらつき）を計算する必要があります。

平方和（ばらつき）の計算を容易にするために、二乗表を作ります。

\[\]

②修正項（CT）を求める

データの二乗表を作成したら、いよいよ平方和の計算になります。

\[修正項(CT)=\frac{(データの合計)^2}{データ数}\]

記事「平方和の式の暗記法」で紹介した、「庭にひくサンプル分のワニ」の「サンプル分のワニ」に該当する部分を計算します。

\[\]

③各平方和（総平方和\(S_T\)、級間平方和\(S_A\)、級内平方和\(S_E\)）を求める

ここで気をつけることは、級間平方和\(S_A\) の求め方です。

級間平方和\(S_A\) は、下の計算式で求められます。

\[級間平方和S_A=\displaystyle \sum_{i=1}^n \frac{(A_i の合計)^2}{A_i のデータ数} – 修正項(CT)\]

修正項(CT)は、「サンプル分のワニ」ですので、平方和の求め方と同じになります。

しかし、引き算される側は、データ数で割り算をしています。

なぜでしょうか？

(。´･ω･)?

理由は、「級間平方和\(S_A\)」を求めているからです。

全体としての二乗の和が知りたいのではなく、水準間のばらつきを級間平方和\(S_A\) で求めています。

そのため、各水準の二乗の平均値を、水準の数だけ足し合わせることで、「（水準間の）二乗の和」を求めています。

\[\]

なお、総平方和\(S_T\) は、水準毎に分けるのではなく、全体のばらつき（平方和）を計算するので、

\[総平方和S_T = \sum (データの二乗)- 修正項(CT)\]

で求められます。

\[\]

④各自由度（総自由度\(Φ_T\)、因子Aの自由度\(Φ_A\)、誤差の自由度\(Φ_E\)）を求める～⑦F検定を行う　

は、回帰分析の時と同じプロセスですので、実例を解きながら確認しましょう。

\[\]

⑧各水準の点平均の推定を行う

異なる水準で実験をしているので、水準の違いによるデータの平均値の違いを計算します。

\[\]

⑨信頼区間の幅を求める

「⑧各水準の点平均の推定を行う」で各水準の点平均値を求めました。

その点平均値を中心に、ある程度の「ばらつき」があるはずです。

その「ばらつき」をt分布を使って、信頼度95%の区間推定を行います。

この時の区間の幅は以下の式で表されます。

\[水準の点平均値±t(Φ_E,0.05)×\sqrt{\frac{V_e}{n}}\]

※\(Φ_E\):誤差の自由　\(V_e\):誤差の不偏分散　\(n\)：各水準毎の観測数

\(n\)は各水準毎の観測数ですので、間違えないようにしましょう！

\[\]

⑩水準間の差を検定する。

水準の違いによる平均値の差と、そのばらつきを計算できたので、\(lsd\) (最小有意差)を計算します。

最小有意差を計算することで、「どの水準間に有意な差があるか」を検討します。

水準間の観測数が同じ場合は、\(lsd\)(最小有意差)は

\[lsd=t(Φ_E,0.05)×\sqrt{\frac{2V_e}{n}}\]

で表されます。

この値より、水準の点平均値の差が大きければ、有意な差がある（水準間で差がある）と判定できます。

\[\]

⑤最小有意差\(lsd\)の計算

さて、先ほど\(lsd\)(最小有意差) は、\(lsd=t(Φ_E,0.05)×\sqrt{\frac{2V_e}{n}}\)　と表しました。

なぜ\(lsd\)(最小有意差) はこの式になるのでしょうか？

(。´･ω･)?

この関係式は「チューキー・クレーマーの方法」から来ています。

※おそらくQC検定２級び出題範囲を超えるので、興味があれば続きを読んでください。

チューキー・クレーマーの方法では、検定統計量\(t_{ij}\) は下式の通りになります。

\[t_{ij}=\frac{|\bar{x_i}-\bar{x_j}|}{\sqrt{V_E(\frac{1}{n_i}+\frac{1}{n_j})}}\]

この検定統計量\(t_{ij}\) が、t表の値よりも大きいときに、帰無仮説である「母平均値に差はない」が棄却され、対立仮説である「母平均値に差がある」が採択されます。

二水準間の観測数が同じ場合、\(n_i=n_j (=n)\) となるので、検定統計量\(t_{ij}\) は、

\[t_{ij}=\frac{|\bar{x_i}-\bar{x_j}|}{\sqrt{\frac{2V_E}{n}}}\]

となります。

比較するt表の値を\(t(Φ_E,0.05)\) とすると、母平均値に差があると判定されるときは、

\[t_{ij}=\frac{|\bar{x_i}-\bar{x_j}|}{\sqrt{\frac{2V_E}{n}}}>t(Φ_E,0.05)\]

\[\large{⇓}\]

\[|\bar{x_i}-\bar{x_j}|>t(Φ_E,0.05)×\sqrt{\frac{2V_E}{n}}\]

これで、\(lsd\)(最小有意差) は計算できました。

\[\]

ところで、この検定統計量\(t_{ij}\) はどこから来たのでしょうか？

正直私はチューキーさんの頭の中がわからないので、正しい答えか自信はありませんが、記事「ポアソン分布の検定と推定」を思い出してみましょう。

この記事では、ポアソン分布の検定統計量\(Z\) を下の式で書きました。

\[Z=\frac{λ_A – λ_B}{\sqrt{λ×(\frac{1}{n_A}+\frac{1}{n_B})}}\]

\(λ_A,λ_B,λ\):単位回数あたりの注目する事象の発生回数

なんかチューキーっぽいですよね。

\[λ_A-λ_B⇒|\bar{x_i}-\bar{x_j}|\qquad λ⇒V_E\]

とすることで、対応関係が分かります。

この検定統計量\(t_{ij}\) がt分布に従う理由は、各水準の観測数を増やせば、測定精度があがること（フィッシャーの三原則）を考えれば納得できます。

\[\]

⑥実例を解いてみる

それでは、最後に問題を解いて確認してみましょう。

問）父,母,私でニャン太君をなでなでした時、ニャン太君の滞在時間（分）を測定した結果、下表の結果となった。

なでなでは、ランダムな順番で行った。分散分析表を作り、水準間に有意な差があるかを検定してください。ただし、有意な差がある場合は、各水準の信頼区間を95%の信頼度で求め、三者間の差があるかを調べよ。

\[\]

ちょっと問題文が長いですが、解いていきましょう。

今回の因子は人（因子Aとします）のみで、三人いるので三水準となります。

人以外の因子はないため、一因子三水準の問題です。

問題文のデータを、下表のように少し手を加えました。

\[\]

①データの二乗表を作る。

二乗表を作ると下表のようになります。

測定データのそれぞれの値を二乗します。

\[\]

②修正項(CT)を求める。

修正項(CT)は下式より求まります。

\[修正項(CT)=\frac{(データの合計)^2}{データ数}\qquad=\frac{65×65}{13}=325\]

\[\]

③各平方和（総平方和\(S_T\)、級間平方和\(S_A\)、級内平方和\(S_E\)）を求める

各平方和を求めていきます。

まずは総平方和\(S_T\)は

\[総平方和S_T = \sum (データの二乗)- 修正項(CT)=403-325=78\]

\(\sum (データの二乗)\) は、①で作成した二乗表を参考にしてください。

次に級間平方和\(S_A\)は

\[級間平方和S_A=\displaystyle \sum_{i=1}^n \frac{(A_i の合計)^2}{A_i のデータ数} – 修正項(CT)\]

\[S_A=\frac{21×21}{5}+\frac{20×20}{5}+\frac{24×24}{3}-325=35.2\]

三つ目の分母だけ「３」ですが、これは私の測定回数が３回のためです。

父と母は５回測定しているので、分母は「５」になります。

最後に誤差平方和\(S_E\)は

\[誤差平方和S_E=総平方和S_T-級間平方和S_A\]

\[S_E=78-35.2=42.8\]

\[\]

④各自由度（総自由度\(Φ_T\)、因子Aの自由度\(Φ_A\)、誤差の自由度\(Φ_E\)）を求める

各自由度を計算すると、下記の通りです。

• 全体の自由度\(Φ_T=総データ数-1 = 13-1=12\)
• 因子Aの自由度\(Φ_A=水準数-1=3-1=2\)
• 誤差の自由度\(Φ_E=Φ_T-Φ_A=12-2=10\)

\[\]

⑤各不偏分散と分散比を求める

以下のように計算できます。

\[V_A=\frac{S_A}{Φ_A}=\frac{35.2}{2}=17.6\]

\[V_E=\frac{S_E}{Φ_E}=\frac{42.8}{10}=4.28\]

\[F_0=\frac{V_A}{V_E}=\frac{17.6}{4.28}=4.112\]

\[\]

⑥分散分析表を作る

以上の計算をまとめると、下表のような分散分析表ができます。

\[\]

⑦F検定を行い、判定する

F表は下の通りです。

分散比\(F_0\) に対して、F検定を行うと、

\[F_0=4.112 \qquad > \qquad F(2,10;0.05)=4.10\]

分散比\(F_0\) がF検定表の値より大きいため、水準間に有意な差が見られると判定できます。

\[\]

⑧各水準の母平均の点推定を行う

水準間に有意な差がみられたので、点推定を行います。

といっても、ただの割り算です。点推定の値は、

• \(A_父=\frac{21}{5}=4.02\)
• \(A_母=\frac{20}{5}=4.00\)
• \(A_私=\frac{24}{3}=8.0\)

\[\]

⑨信頼区間の幅を求める

信頼区間を信頼度95%で求めます。

信頼区間の幅は、\(水準の平均±t(Φ_E,0.05)×\sqrt{\frac{V_E}{n_i}}\) で求められます。

※\(n_i\) ：各水準ごとの観測数

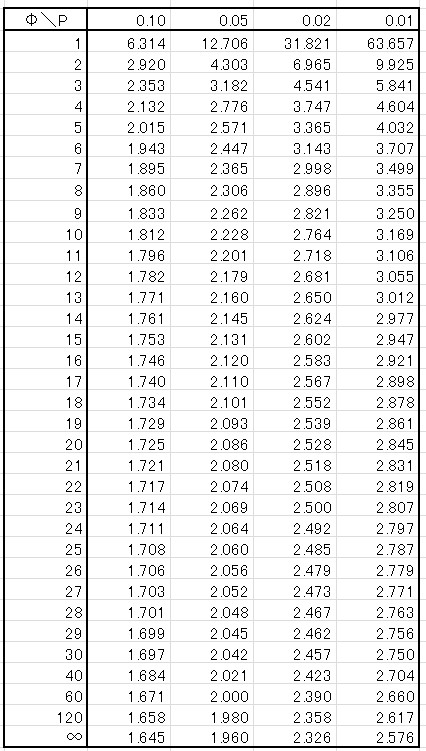
t表より、\(t(10,0.05)=2.228, V_E=4.28\) なので、計算すると、

\(A_父\)水準の母平均の区間推定は、\(4.02±2.06\)

\(A_母\)水準の母平均の区間推定は、\(4.00±2.06\)

\(A_私\)水準の母平均の区間推定は、\(8.00±2.66\)

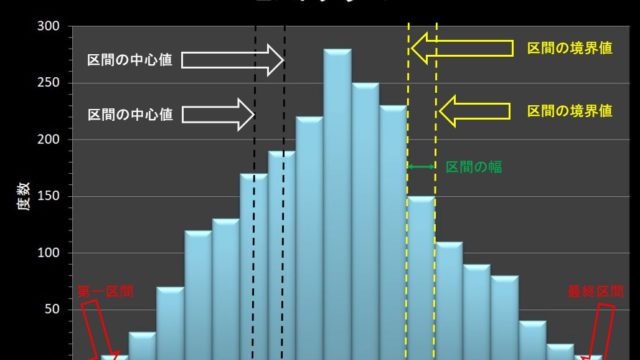
この結果を図示すると、下図のようになります。

図を見てわかることは、\(A_私\)の中心値が大きいことがわかりますが、信頼区間の幅も大きいことが分かります。

信頼区間の幅が大きい理由は、観測数が水準父と水準母に比べて少ないため、データの精度が悪いからです。

\[\]

⑩水準間の差を検定する

QC検定２級の出題範囲を逸脱している気もしますが・・・

水準間の差を検定してみます。

ただし、水準\(A_私\) の観測数が水準\(A_父\)と水準\(A_母\)より少ないため、\(lsd=t(Φ_E,0.05)×\sqrt{\frac{2V_e}{n}}\) が使えません。

チューキー・クレーマーの方法で検定統計量\(t_{ij}\) を考えてみます。

\[|A_父-A_母|=0.02 \qquad |A_父-A_私|=3.98 \qquad |A_母-A_私|=4.00\]

\[lsd’_1=t(10,0.05)×\sqrt{4.28×(\frac{1}{5}+\frac{1}{3})}\]

\[lsd’_1=2.228×\sqrt{\frac{34.24}{15}}=3.366\]

\[lsd’_2=t(10,0.05)×\sqrt{4.28×(\frac{1}{5}+\frac{1}{5})}\]

\[lsd’_2=2.228×\sqrt{\frac{8.56}{5}}=2.915\]

\(lsd’_1\) は「父ー私、母ー私」を比較した時の最小有意差で、\(lsd’_2\) は「父ー母」を比較した時の最小有意差になります。

計算結果をまとめると、下の関係が成り立ちます。

\[|A_父-A_母|<lsd’_2 \qquad |A_父-A_私|>lsd’_1 \qquad |A_母-A_私|>lsd’_1\]

ということで、「父と母の間になでなでの有意な差があるとは言えないが、父と私、または、母と私の間にはなでなでに有意な差がある」　ということが分かりました。

やったね！ヾ(´∀｀)ﾉ

有意差については、信頼度95%の範囲を表した図を見ても直感的に理解できますね。

\[\]

まとめ

①実験計画法とは、少ない検証数で一番良い水準を見極めること

②フィッシャーの三原則は「反復、無作為、局所管理」

③分散分析法では、「級間変動＞級内変動」を確認

④分散分析の手順は、回帰分析の時とほぼ同じ

⑤最小有意差\(lsd\)は、チューキー・クレーマーの方法からきてるっぽい

⑥実例を解いてみよう

\[\]

今回は実験計画法の基礎と一元配置の問題を解きました。

次回も引き続き実験計画法を勉強しますが、二元配置実験について勉強していきます。

\[\]

⇒オススメ書籍はこちら

⇒サイトマップ