回帰分析とは

公開日2020年7月20日 　最終更新日 2021年9月20日

みなさんこんにちは、michiです。

前回の記事では「大波の相関、小波の相関」を学びました。

今回は回帰分析について勉強していきます。

前回学んだ相関分析と異なり、「回帰直線」を想定して分析します。

キーワード：「回帰直線」「残差」「最小二乗法」

①回帰分析とは

回帰分析とは、説明変数\(x\) （独立変数）と目的変数\(y\)（従属変数）との定量的な関係を求めることです。

記事「相関関係1　相関係数とは」で学んだ相関関係との違いは、目的変数\(y\) を説明変数\(x\) で説明しようとすることです。

(。´･ω･)?　どゆこと？

相関関係は、二者を比べ、片方が増加すればもう片方も増加する、といった傾向を判断するものでした。

それが回帰分析では、「説明変数\(x\)が○％増加したら、目的変数\(y\)は△％増加するだろう」　という仮定を検証します。

なおQC検定２級では、説明変数\(x\) が一つだけの単回帰が出題範囲となっていて、説明変数\(x\) が二つ以上の重回帰は出題範囲とはなりません。

\[\]

②回帰式の意味

「①回帰分析とは」で「説明変数\(x\)が○％増加したら、目的変数\(y\)は△％増加するだろう」と説明しましたが、これを数式化すると以下の式になります。

\[y_i=α+βx_i+ε_i\]

\(α\)：常数（切片）、\(β\)：母回帰係数、\(ε_i\)：残差変量

\(x_i,y_i,ε_i\)は、\(i\) 番目の\(x,y,ε\)をそれぞれ表し、全体で\(n\)番目まであるとします。

このように、左辺の目的変数\(y_i\) が右辺の説明変数\(x_i\) と常数、母回帰係数、残差変量で表されます。

\[\]

中学の数学で比例の関係を学んだ方も多いと思います。

その時は、\(y=ax+b\) （\(αとb、βとaが対応\)）と書いていたかもしれません。

紛らわしいですが、今回はテキストに従って、\(y_i=α+βx_i+ε_i\)　とさせていただきます。

では、式　\(y_i=α+βx_i+ε_i\)　を少しずつ分解しながら意味を考えてみましょう。

\[\]

１．\(y_i=βx_i\) の時

このときのグラフは下図のようになります。

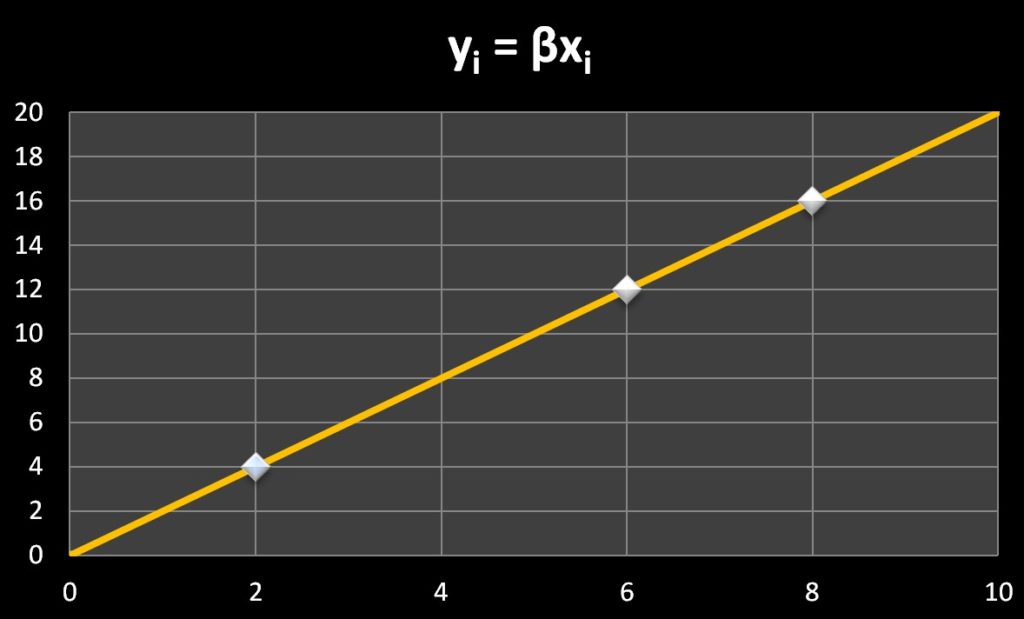
このように、説明変数\(x_i\) が増加すると、目的変数\(y_i\)が比例の関係で決まります。

この時のグラフの傾き（増え方）は\(β\)で決まります。

ただし、この式には欠点があります。

それは「0」を通ってしまうことです。

例えば、回帰分析の結果、労働時間と売り上げに比例の関係がある場合を考えます。

回帰式が、\(y_i=βx_i\)　の時は、労働時間「0」という前提があることになります。

労働時間「0」という前提は考えづらいです。

そのため、常数（切片）\(α\) を使います。

\[\]

　2．\(y_i=α+βx_i\) の時

常数（切片）\(α\) を足すことで、比例関係は下図のようにうまく表現できました。

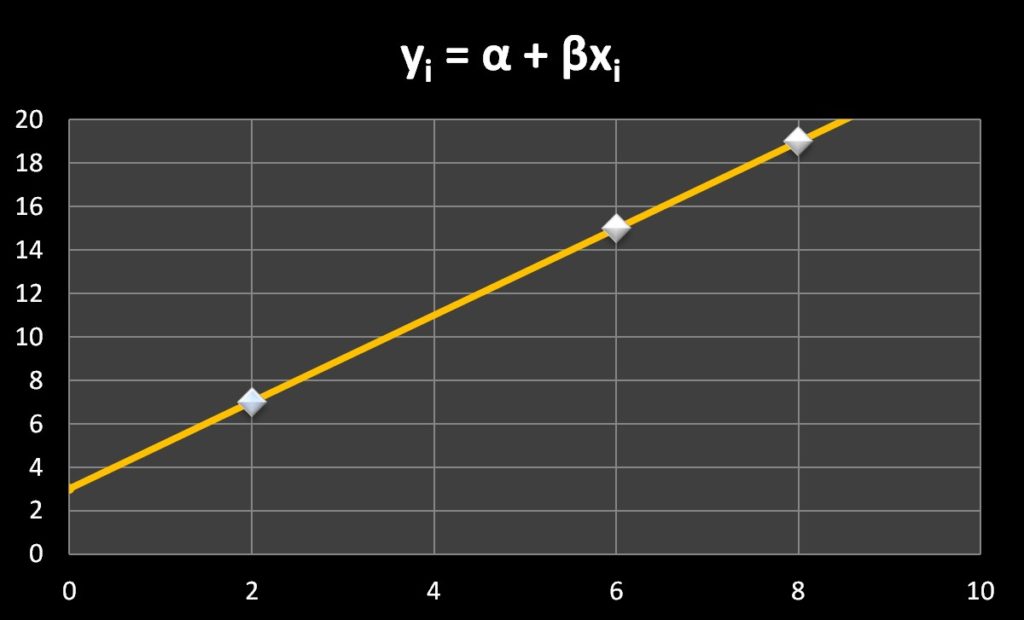
(★´･ω･)oｵｯ(☆｀･ω･)=b ヶ～♪

ところが、回帰式\(y_i=α+βx_i\)　では実際のデータをうまく反映できていません。

なぜなら、各測定データに対して「ばらつき」を考慮していないためです。

(。´･ω･)?

どういうことでしょうか？

回帰式\(y_i=α+βx_i\)　で表されるデータというのは、「一直線上」に分布しているデータです。

実際の測定データが説明変数\(x_i\) に対し目的変数\(y_i\) が「一直線上」に分布することはまずありえません。

そこで、個々の測定データの回帰式からの「ばらつき」を考えます。

\[\]

　3．\(y_i=α+βx_i＋ε_i\) の時

この式はこの章の冒頭に出てきた式です。

この時の様子は下図のようになります。

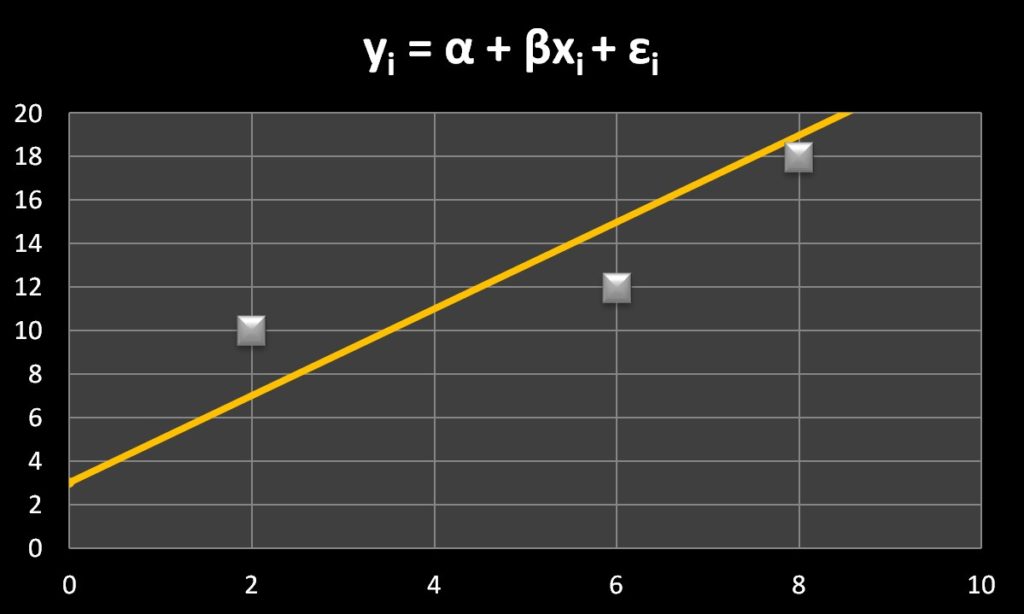
この図を見ると、新たな疑問が出てきます。

どうやって直線を引くのか？　です。　

全てのデータが一直線上に並んでいるときは、簡単に見つかりそうです。

しかし普通の測定データのように「ばらつき」がある場合はそうすればよいのでしょうか？

(。´･ω･)?　

答えは、「ばらつき」のある実測データの全体を見て、真ん中らへんを通ている直線（回帰直線）を引く　です。

\[\]

・・・ちょっと何言ってるかわかりませんね。

もう少し言い方を変えると、「真ん中らへんを通っている直線（回帰直線）と各実測データとの差（ばらつき）が最小になるような線を引く」　です。

では、どうやって真ん中らへんを通る直線を決めるかというと、「最小二乗法」を使います

\[\]

※回帰直線自体は、常数\(α\) と母回帰係数\(β\) で決まる一つの直線になります。

回帰直線には「ばらつき」を表す残差変量\(ε_i\) は現れないので、気をつけましょう！

___φ(ﾟｰﾟ*)ﾌﾑﾌﾑ___φ(｡_｡*)ｶｷｶｷ ΣΣﾋﾞﾘｯ!!___ φ(ﾟдﾟ｀)

\[\]

③最小二乗法によるパラメータの計算

注意）この章はメチャクチャ長い文章で、高校数学の知識を使う計算がでてきます。

最小二乗法を使う目的は、残差変量\(ε_i\)(=ばらつき)のあるデータから、回帰直線を求めることです。

イメージは下の図になります。

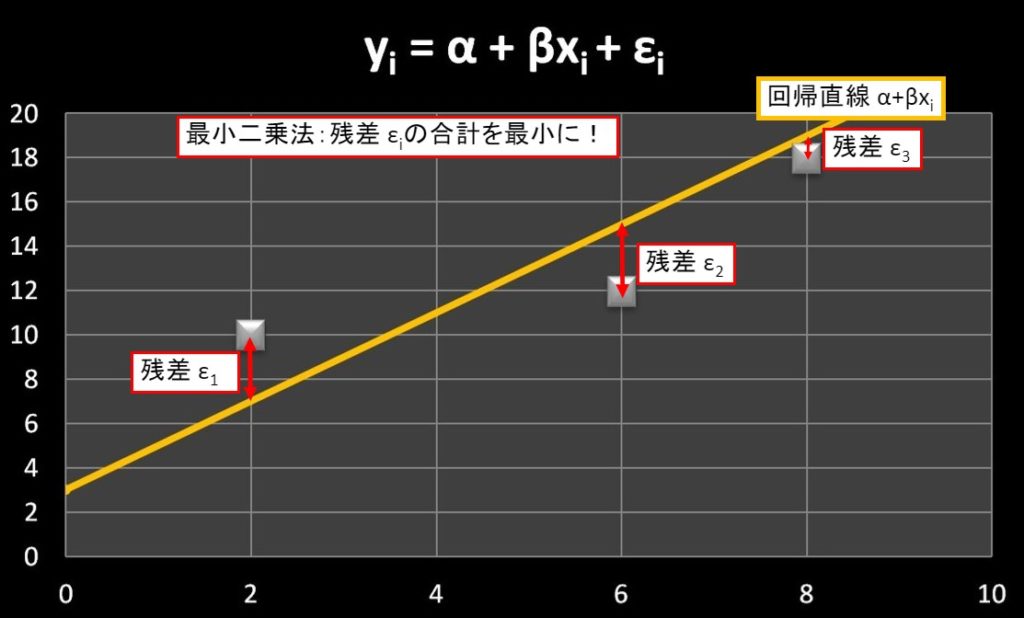
始めに、回帰直線の式を変形させて、残差変量\(ε_i =\) の形にします

\[y_i=α+βx_i＋ε_i　\qquad ⇒ ε_i = y_i -(α+βx_i)\]

次に名前にもある通り、上の計算式を二乗します。

なぜ二乗するのかについては、記事「平方和の式の暗記法」をご参照ください。

※簡単に言うと「マイナス側のばらつきも計算するため」です。　

すると、計算式は、

\[(ε_i)^2 = (y_i -(α+βx_i))^2\]

この式を全ての実測データ(\(n\)番目のデータまで)に適用するために「 \(\sum\) 」を使います。

\[\sum_i(ε_i)^2 = \sum_i(y_i -(α+βx_i))^2\]

\[\sum_i(ε_i)^2 = \sum_i(y_i^2 -2(α+βx_i)y_i+(α^2+2αβx_i+β^2X_i^2))\]

\[\]

次に、\(α\)、\(β\)のそれぞれに対して、偏微分を行います。

(´･ω･)?(･ω･｀)

偏微分は、簡単に言うと「複数の変数がある式で、一つの変数に対して微分をすること」になります。

例えば、\(α\)に対して偏微分をする場合は、\(β\)は定数とみなします。

微分が何かといわれると・・・「変化量の計算をしている」と考えてください。

つまり、\(α\)、\(β\)それぞれに対して偏微分を行うことで、\(α\)、\(β\)それぞれの「変化量」を計算しています。

この変化量が最小になるときが、残差変量\(ε_i\) が最小になるときです。

※今回の残差変量の二次方程式は下に凸なグラフになるので、変化量が最小の時が、残差変量\(ε_i\) が最小になります。

\[\]

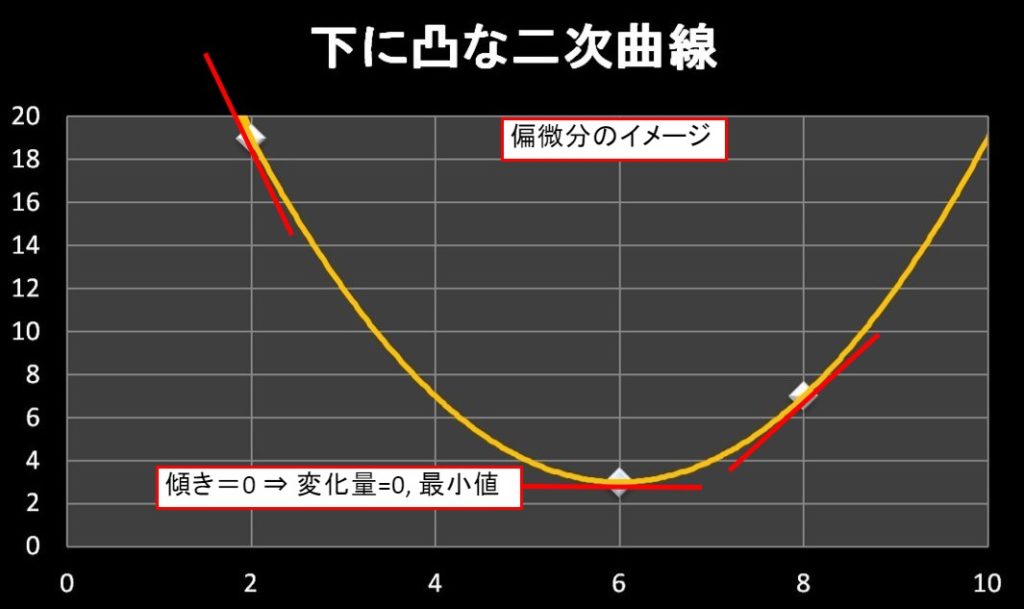
計算に戻ります。まずは\(α\)に対しての偏微分です。

\[\displaystyle \frac{\partial}{\partial α}\sum_i(ε_i)^2 =\displaystyle \frac{\partial}{\partial α} \sum_i(y_i^2 -2(α+βx_i)y_i+(α^2+2αβx_i+β^2x_i^2))\]

\[\displaystyle \frac{\partial}{\partial α} \sum_i(α^2 +(2βx_i-2y_i)α+ y_i^2 -2βx_i y_i+β^2x_i^2)\]

\[=\sum_i(2α+2βx_i-2y_i) =2\sum_i(α+βx_i-y_i)\]

\(\displaystyle \frac{\partial}{\partial α}\sum_i(ε_i)^2=0 \)の時が最小値となるので、

\[\sum_iα+\sum_iβx_i-\sum_iy_i=0\]

ここで、\(\sum_iα\) は\(α\)を\(n\)回足し算していることを意味するので、　\(\sum_iα = αn\)

また、\(β\) は\(α\)を変数とみているため、定数扱いとなります。

よって、

\[\sum_i α+\sum_i βx_i – \sum_i y_i=0　\qquad ⇒ αn =\sum_i y_i – β\sum_i x_i\]

\[\]

(⌒(´-ω-)_

もうひと頑張り！

\(\sum_i x_i\)と\(\sum_i y_i\)は、各データ\(x_i\)と\(y_i\)を \(i=1～n\) までを足した合計です。

\(\sum_ix_i\)と\(\sum_i y_i\)をそれぞれデータ数\(n\)で割り算すると・・・平均になりますよね！？　よって

\[αn =\sum_i y_i – β\sum_i x_i \qquad ⇒　α=\bar{y}-β \bar{x} \]

※\(\bar{x}\):\(x\)の平均、\(\bar{y}\):\(y\)の平均

常数（切片）\(α\) は、母回帰係数\(β\)　と\(x,y\)の平均値\(\bar{x},\bar{y}\) で求めることができました。

\[\]

さて、次に母回帰係数\(β\) について偏微分を行います。すると、

\[\displaystyle \frac{\partial}{\partial β}\sum_i(ε_i)^2 =\displaystyle \frac{\partial}{\partial α} \sum_i(x_i^2β ^2+(2αx_i-2x_iy_i)β+y_i^2+2αy_i+α^2))\]

\[=\sum_i(2x_i^2β+2αx_i-2x_iy_i) =2\sum_i(x_i^2β+αx_i-x_iy_i)\]

先ほどと同様に、\(\displaystyle \frac{\partial}{\partial β}\sum_i(ε_i)^2=0 \)の時が最小値となるので、

\[\sum_i(x_i^2β+αx_i-x_iy_i)=0\]

\(α\)の偏微分の結果より、

\[α=\frac{\sum_iy_i}{n}-β\frac{\sum_ix_i}{n}\]

\(α=・・・\)を代入して、

\[\sum_i(x_i^2β+αx_i-x_iy_i)=0 \]

\[ \sum_i x_i^2β+(\frac{\sum_iy_i}{n}-β\frac{\sum_ix_i}{n})\sum_i x_i-\sum_i x_iy_i)=0 \]

\[(\sum_i x_i^2 – \frac{(\sum_ix_i)^2}{n})β +\frac{(\sum_i x_i)(\sum_iy_i)}{n} – \sum_i x_iy_i =0 \]

\[β=\frac{\sum_i x_iy_i-\frac{(\sum_i x_i)(\sum_i y_i)}{n}}{\sum_i x_i^2 – \frac{(\sum_ix_i)^2}{n}}\]

\[\]

ヽ(τωヽ)ﾉ ﾓｳﾀﾞﾒﾎﾟ

せっかく、ここまで計算できたのに、諦めるのはもったいない！

実はこの式は平方和の式になっています。

分母の\(\sum_i x_i^2 – \frac{(\sum_ix_i)^2}{n}\) は\(x\)の平方和\(S_x\) を、分子の\(\sum_i x_iy_i-\frac{(\sum_i x_i) (\sum_i y_i)}{n}\) は、\(xy\)の偏差積和\(S_{xy}\) を表します。よって、

\[β=\frac{S_{xy}}{S_x}\]

このように、かなりシンプルにまとまります。

Σ(*´･ω･ﾉ)ﾉ

母回帰係数\(β\) は、\(x\)の平方和\(S_x\)と\(xy\)の偏差積和\(S_{xy}\)で求めることができました。

\[\]

長かったですが、以上をまとめると、

\[α=\bar{y}-β \bar{x},\qquad β=\frac{S_{xy}}{S_x}\]

\[\]

④回帰直線と残差変動の関係

「③最小二乗法によるパラメータの計算」で、回帰直線　\(y=α+βx\) を求めることができるようになりました。

本来やりたいのは、回帰直線からの「ばらつき」である残差変動の評価です。

「ばらつき」に対して、以下の関係式が成り立ちます。

　\[全体の変動（S_T）=回帰による変動（S_R）+残差による変動（S_E）\]

全体の変動とは、測定して得られたデータ全体のことを言います。

全体の変動は、回帰直線による変動と、その回帰直線からのずれ（残差）で表されます。

\[\]

記事「平方和の式の暗記法」では、「ばらつき」の評価に平方和を使いました。

今回もその時と同様に、平方和で「ばらつき」を考えます。

全体の変動(\(S_T\))は、測定された目的変数\(y\) の変動のことなので、

\[S_T = S_y\]

回帰式による各目的変数\(y\)の値は、\(\sum_i y_i=α+β\sum_i x_i\) です。

回帰式による各目的変数\(y\)の値と\(y\)の平均値との差分の二乗（＝平方和）が、回帰による変動になるので、

\[S_R=(\sum_i y_i – \bar{y})^2\]

\(\sum_i y_i=α+β\sum_i x_i\)、最小二乗法より、\(α=\bar{y}-β\bar{x}\) なので、

\[S_R=(\bar{y}-β\bar{x}+β\sum_i x_i- \bar{y})^2\]

\[S_R=(\sum_i x_i – \bar{x})^2 β^2\]

\(β\) は母回帰係数なので、()の外に出しました。

\((\sum_i x_i – \bar{x})^2\) は\(x\)の平方和\(S_x\) のことなので、

\[S_R=β^2S_x\]

最小二乗法より、\(β=\frac{S_{xy}}{S_x}\) なので、

\[S_R=\frac{(S_{xy})^2}{S_x}\]

\[\]

最後に残差による変動ですが、下の関係式より、

　\[全体の変動（S_T）=回帰による変動（S_R）+残差による変動（S_E）\]

\[S_E=S_T-S_R =S_y-\frac{(S_{xy})^2}{S_x}\]

となります。（絶対覚えましょう）

残差変動は、全体の変動から回帰による変動を引いて、求めます。

\[\]

まとめ

①回帰分析は、目的変数\(y\) を説明変数\(x\) で説明しようとすること

②回帰式は、\(y_i=α+βx_i+ε_i\)　

③最小二乗法より、\(α=\bar{y}-β \bar{x},\qquad β=\frac{S_{xy}}{S_x}\)

④　\(全体の変動（S_T）=回帰による変動（S_R）+残差による変動（S_E）\)

\[S_E=S_T-S_R =S_y-\frac{(S_{xy})^2}{S_x}\]

\[\]

今回は理論的な話が中心になってしまいました。

次回は回帰分析の手順を具体例をあげて、実際に問題を解いてみたいと思います。

また、寄与率についてもまとめます。

ではまた次回もよろしくお願いいたします。

⇒オススメ書籍はこちら

⇒サイトマップ