指数分布 とは

公開日2021年9月12日 最終更新日 2021年10月10日
みなさんこんにちは、michiです。
前回の記事ではサンプリングの種類と計算方法について学びました。
今回は指数分布について学んでいきましょう。
キーワード:「ポアソン分布」「MTTF」
目次
①指数分布とは
指数分布は「ある事象が発生するまでの時間の分布」を表します。
指数分布の確率密度関数は、次の式で与えられます。
\[f(x)=λe^{-λt} \qquad(t≧0)\]
\[f(x)=0 \qquad(t≦0)\]
\[\]
パラメータ \(λ\) は単位時間あたりの何かしらの事象の発生回数を表します。
何かしら事象が故障であれば、\(λ\) は故障率になります。
例えば、 \(λ=3\) とすると、次のようになります。
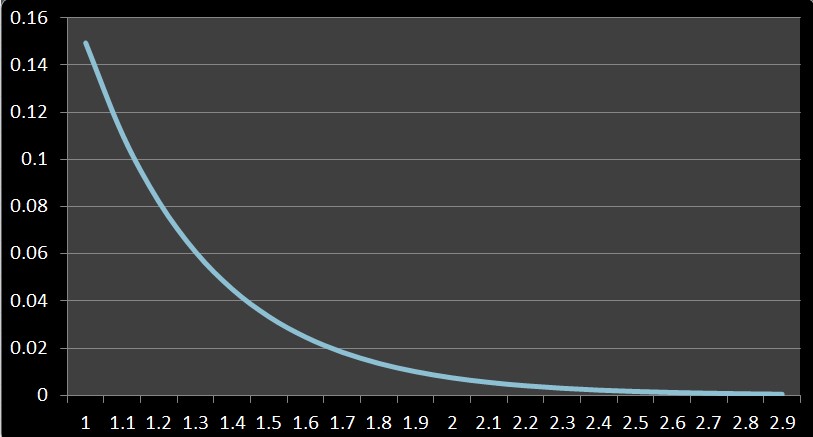
時間とともに故障率が指数関数的に下がっています。
これは、時間の経過とともに故障しない(正常である確率)確率が下がることを意味します。
\[\]
確率密度 \(f(x)\)は、ある事象が発生するまでの待ち時間 \(X\) の累積分布関数を微分することで求めることができます。
待ち時間 \(X\) の累積分布関数 \(F(X)\) は、ポアソン分布を用いて計算します。
ポアソン分布では、ある事象が発生しない確率 \(P\) を使います。
すると、
\[F(t)=1-P \qquad (X>t)\qquad = 1-e^{-λt}\]
となります。
\[\]
ポアソン分布の確率の計算は、記事「ポアソン分布について」より以下のように書けます。
\[P=\frac{λ^x e^{-λ}}{x!}\]
- \(x\) : 発生回数
発生回数 \(x\) が0の場合を考えると、
\[P=\frac{λ^x e^{-λ}}{x!}=\frac{λ^0 e^{-λ}}{0!}=e^{-λ}\]
となります。
\[\]
これを任意の時間 \(t\) の関数として考えると、累積分布関数 \(F(t)\) は、
\[F(t)=1-e^{-λt}\]
累積分布関数 \(F(t)\) を微分することで確率密度関数 \(f(t)\)が求まります。
\[\]
さて、指数分布のイメージができたので、指数分布の期待値と分散を考えていきましょう。
\[\]
②指数分布の期待値の導出
指数分布の期待値 \(E(x)\) は次の式で求められます。
\[E(x)=\int_{-\infty}^{\infty}xf(x)dx\]
\(x→t\) とし、指数分布は確率密度関数 \(f(x)\) は \(f(x)=λe^{-λx}\) \( (x≧0)\) となるので、
\[E(x)=\int_{-\infty}^{\infty}xf(x)dx=\int_{-\infty}^{\infty}xλe^{-λx}dx\]
\[=\int_{0}^{\infty}xλe^{-λx}dx\]
※指数分布では \(x<0\) は0となるため
あとは部分積分法を使うと、
\[E(x)=\int_{0}^{\infty}xλe^{-λx}dx\]
\[=\left[ -xe^{-λx} \right]_{0}^{\infty}+\int_{0}^{\infty}e^{-λx}dx\]
ここで、 \(\left[ -xe^{-λx} \right]_{0}^{\infty} ⇒0\) となるので、
\[E(x)=\int_{0}^{\infty}e^{-λx}dx=\left[ -\frac{1}{λ}e^{-λx} \right]_{0}^{\infty}=0+\frac{1}{λ}e^0=\frac{1}{λ}\]
となります。
\[\]
途中計算は厄介ですが、最終的にはかなりシンプルな形になりました。
部分積分法がよくわからなくても気にしないでください。
指数分布の期待値 \(E(x)\) ⇒ \(\frac{1}{λ}\) ! これで十分です。
φ(´・ω・`)メモメモ

\[\]
③指数分布の分散の導出
指数分布の期待値を考えたので、次は分散について考えます。
分散は次の式で求められます。
\[V(x)=\int_{-\infty}^{\infty}(x-μ)^2f(x)dx\]
\(μ\)は、期待値 \(E(X)\) なのですが、このままだと少し扱いづらいです。
そこで、式変形をします。
\[\]
\[V(x)=\int_{-\infty}^{\infty}(x-μ)^2f(x)dx\]
\[=\int_{-\infty}^{\infty}(x^2-2xμ+μ^2)f(x)dx\]
\[=E(x^2)-2μE(x)+μ^2\]
\[\]
\(μ = E(x)\) だから、
\[V(x)=E(x^2)-2μE(x)+μ^2\]
\[=E(x^2)-2μ^2+μ^2\]
\[=E(x^2)-μ^2\]
\[=E(x^2)-(E(x))^2\]
指数分布の期待値 \(E(x)\) は先ほど計算したので、\(E(x^2)\) を計算します。
期待値の導出時と同様に部分積分法を使うと、
\[E(x^2)=\int_{0}^{\infty}x^2λe^{-λx}dx\]
\[=\left[ -x^2e^{-λx} \right]_{0}^{\infty}+\int_{0}^{\infty}2xe^{-λx}dx\]
\[=2\int_{0}^{\infty}\frac{1}{λ}λxe^{-λx}dx\]
\(λ\) は定数なので、積分の前に持ってきます。
\(\int_{0}^{\infty}λxe^{-λx}dx\) は、先ほど計算した期待値 \(E(x)\) と同じ形になります。
よって、\(E(x^2)\) は次のように計算できます。
\[E(x^2)=\frac{2}{λ}\int_{0}^{\infty}λxe^{-λx}dx\]
\[=\frac{2}{λ}E(x)=\frac{2}{λ^2}\]
\[\]
かなり導入が長かったですが、指数分布の分散 \(V(x)\) を求めてみます。
\[V(x)=E(x^2)-(E(x))^2=\frac{2}{λ^2}-\left(\frac{1}{λ}\right)^2=\frac{1}{λ^2}\]
\[\]
指数分布の分散もかなりシンプルになりました。
分散の式の導出はかなり厄介ですが、期待値と同様に結果を覚えておけば試験本番は大丈夫です。
指数分布の分散 \(V(x)\) ⇒ \(\frac{1}{λ^2}\) ! これでいきましょう!
φ(´・ω・`)メモメモ 💦

\[\]
④指数分布の故障率
指数分布の期待値と分散について学びました。
どうも指数分布では「\(\lambda\)」が重要になりそうです。
というより、「\(λ\)」だけ知っていれば良さそうです。
\[\]
ところで、この「\(λ\)」は何者なのでしょうか?
(。´・ω・)?
「①指数分布とは」では、ポアソン分布から指数分布を考えました。
ポアソン分布において \(λ=np\) とすると、これはポアソン分布の期待値を表すものでした。
\(n=1\) の場合を考えると、「\(λ\) はある事象が発生する確率 \(p\)」 と同じになります。
\[\]
指数分布は”ある事象”が発生するまでの時間を表すので、2回目以降の発生を考える必要がありません。
すなわち、最初の1回 \(n=1\) の場合を考えればよいことになります。
すると、「\(λ\) はある事象が発生する確率 \(p\)」と同じであることがわかります。
\[\]
さて、この”ある事象”についてもう少し考えてみます。
問題の定義にもよりますが、品質保証の場合は”ある事象”とは”製品の故障”とされることが多いです。
そのように定義すると、「\(λ\) は製品の故障が発生する確率」⇒「\(λ\) は製品の故障率」となります。
(。 ・ω・))フムフム
\[\]
最後にもう少し深く考えてみましょう。
記事「信頼性工学 1」に書いたように、平均故障時間MTTFは故障率の逆数になります。
したがって、製品のMTTFは故障率の逆数 \(\frac{1}{λ}\) となります。
なんと、指数分布の期待値と同じになりました。
\[\]
少し不思議な気もしますが、指数分布は「ある事象が発生するまでの時間の分布」を表しています。
指数分布の期待値は「ある事象が発生するまでの期待される時間」⇒「ある事象が発生するまでの平均時間」となります。
「ある事象」を故障と考えると、指数分布の期待値は「故障発生までの平均時間」となります。
「故障発生までの平均時間」すなわちMTTFのことです。

\[\]
まとめ
①指数分布の確率密度関数は以下の式で表されます。
\[f(x)=λe^{-λt} \qquad(t≧0)\]
\[f(x)=0 \qquad(t≦0)\]
②指数分布の期待値 \(E(x)\) ⇒ \(\frac{1}{λ}\) !
③指数分布の分散 \(V(x)\) ⇒ \(\frac{1}{λ^2}\) !
④製品のMTTFは故障率の逆数 \(\frac{1}{λ}\)
\[\]
指数分布はQC検定2級までは全くでてきませんでしたが、QC検定1級ではちらほら出てきます。
実践的な場面では案外、指数分布を目にします。
QC検定1級の範囲だから、やらなくても良い!ではなく、実践で使えそうだから学ぶ!の心持ちで行きましょう!
\[\]















