平均=普通?

公開日2020年1月21日 最終更新日 2021年9月20日
みなさんこんにちは、michiです。
今回のテーマ「平均=普通?」について学んでいきます。
・・・平均って普通のことでしょ?といままでの経験から答えは出てそうです。
果たして実際はどうなのか、勉強していきます。
QC検定でも出題される基礎的な内容になります。
キーワード 「平均値」「中央値(メディアン)」「最頻値(モード)」
目次
①平均値とは
突然ですが、みなさん「平均値」はご存知でしょうか?
おそらく多くの人がご存知でしょう。みなさんが一番慣れ親しんでいる統計値の一つだと思います。
計算式は、次の通りになります。
\[平均値 = データの合計 ÷ データの数\]
\[\]
では、次の質問です。
日本人(10歳以上)一人当たりの一日の平均勉強は何時間でしょうか?
┐(‘~`;)┌ シラネ
\[\]
答えは、“全年代で考えると” 一日の平均勉強時間は約13分です(下図)。
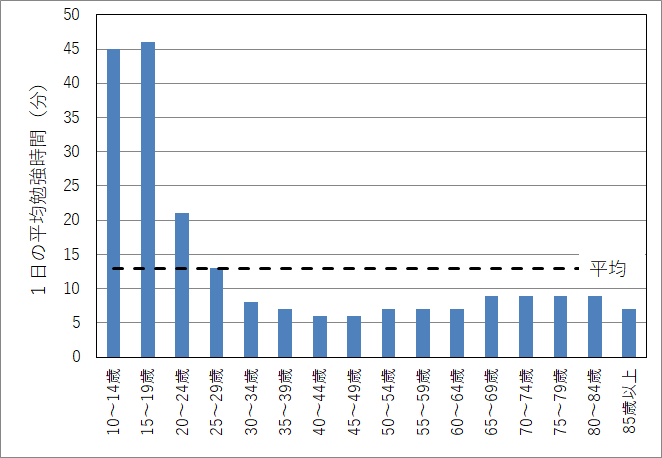
(社会生活基本調査、平成28年社会生活基本調査、調査票Aに基づく結果、生活時間に関する結果、主要統計表、票番号1-1より)
\[\]
グラフを見ると、学生世代(10~24歳)が勉強時間の平均を押し上げていることが分かります。
30代以上の全世代が平均以下の勉強時間ですので、「平均=普通」と考えると、30代以上の全世代はすべて普通ではないことになります。
世代別平均勉強時間の調査結果からわかるように、データのばらつきの差が大きい場合や、極端な値があると「平均=普通」と考えづらくなります。
※この傾向は年収や保有資産などのデータにもあらわれます。
\[\]
では、何を普通とすればよいのでしょうか?
その答えの手がかりに「中央値」と「最頻値」という考えがあります。
\[\]
②中央値とは
「中央値(メディアン)」は、値を大小順に並べていき、その中央に来る値です。
\[\]
例えば、何か実験をして得られたデータが次の通りだったとします。
得られたデータ 「\(1,3,5,5,5,7,7,8,13\)」
このとき、得られたデータ数は9個(奇数)なので、小さい順で5番目と大きい順で5番目の値は同じ値になります。
今回の場合は、\(\boldsymbol{5}\) になりますね。
得られたデータ 「\(1,3,5,5,\boldsymbol{5},7,7,8,13\)」
\[\]
では、得られた全データ数が偶数の場合はどうでしょうか?
得られたデータ 「\(1,3,5,5,5,7,7,8,13,21\)」
このとき、全データ数は10個(偶数)なので、奇数の時のように得られたデータの中に中央値はありません。
では、どうすればよいのか?というと、間を取ります。
\[\]
今回の例の場合は、\(\boldsymbol{5,7}\) になりますね。
得られたデータ 「\(1,3,5,5,\boldsymbol{5,7},7,8,13,21\)」
つまり、その間を取るわけですから、中央値は
\[中央値=\qquad \frac{5+7}{2}=\qquad 6\]
以上が中央値の考え方です。
ちなみに、得られたデータが上記「\(1,3,5,5,5,7,7,8,13,21\)」の平均値は、「7.5」となります。
中央値より少し大きな値です。
これは、「21」という大きなデータが全体の平均値を押し上げているためです。
\[\]
③最頻値とは
「最頻値(モード)」は、データの中で一番多く出てくる値のことになります。
中央値の説明で使用した得られたデータをもう一度見てみましょう。
得られたデータ 「\(1,3,5,5,5,7,7,8,13,21\)」
\[\]
この時の最頻値は \(\boldsymbol{5}\) になります。
なぜなら、\(5\) が得られたデータ(全10回)の中で一番多く出てくる数字だからです。
\[\]
データの分布に偏りがある場合、一般的に
データが小さいほうに偏っている場合は、「最頻値<中央値<平均値」
データが大きいほうに偏っている場合は、「平均値<中央値<最頻値」
となります。
\[\]
④日本人の平均勉強時間を考える
さて、「平均値、中央値、最頻値」を学んだので、冒頭のデータをもう一度見直してみましょう。
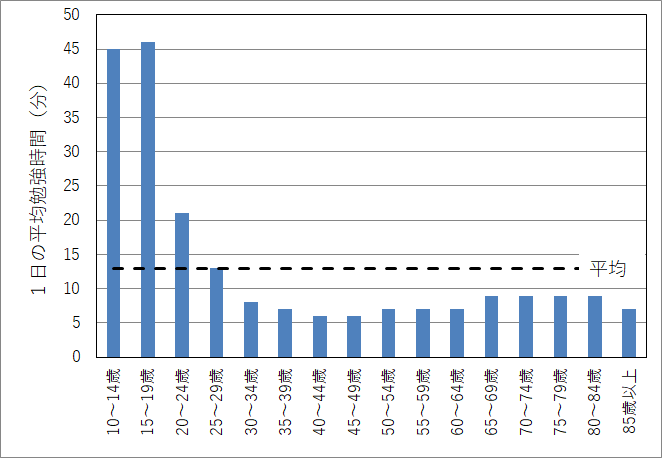
平均値の説明では、平均の勉強時間が約13分になりました。
この時の中央値は9分 最頻値が7分となります。
どうでしょうか?平均値よりも中央値や最頻値の方が、がグラフ的にも「普通」っぽいですよね?
これで日本人の1日の「普通」の勉強時間がわかった! と思いませんでしたか?
(。´・ω・)?チガウノ?
\[\]
実はこのデータから得られる中央値の9分や、最頻値の7分という値もまた、各世代の「平均値」なのです。
「30~34歳の平均勉強時間が7分」ということが、このデータからはわかりますが、極端に言うと次の場合が考えられます。
- 70分勉強している人 1人+0分勉強している人(勉強していない人) 9人
- 7分勉強している人 10人
どちらの方が現実的でしょうか?
集団全員が7分きっかり勉強していると考えるより、「勉強している人としていない人がいる」と考えるほうが自然ではないでしょうか。
つまり、「30~34歳の平均勉強時間が7分」は、勉強時間0時間の人たちが、勤勉な人たちの足をひっぱっている結果かもしれないのです。
\[\]
みなさん、「平均=普通」とは限りません!
「このデータの平均値は・・・」という人にあったら、「中央値と最頻値は?」と聞いてみましょう。
真実が見えてくるかもしれません。
※平均値が全体を表している場合も、もちろんありますよ
\[\]
⑤まとめ
①平均値=全データの合計÷データ数
②中央値=大小順番に並べ、両端から数えて真ん中に来る値
③最頻値=全データの中で一番多く出てくる値
④日本人の平均勉強時間は13分だけど、現実を表してはいない
\[\]
これから学んでいくQC検定などの多くの統計学では、「平均値」が頻繁に使われます。それは、正規分布に従うことを前提にしたデータ解析が多いためです。
次回は「平方和の式の暗記法」をテーマに、平方和について勉強していきましょう!














