t分布とは

公開日2020年4月30日 最終更新日 2022年6月26日
みなさんこんにちは、michiです。
前回はF分布について学びました。
簡単にF分布をおさらいすると、同一の母分散を持つ二つの標本の「ばらつき」を評価するものでした。
今回のテーマのt分布は、正規分布と同様に標本の平均について評価します。
キーワード「t分布」「標準化した統計量Zとの違い」
目次
①t分布とは
t分布とは、「標本の平均を評価するための検定統計量」です。
t分布の統計量の定義は以下の通りです。
\[t= \frac{\bar{x}-μ}{\sqrt{\frac{V}{n}}}\]
※\(\bar{x}\)は標本の平均値、\(μ\)は母平均、\(V\)は不偏分散、\(n\)はサンプル数をあらわします。
この時の\(\sqrt{\frac{V}{n}}\) を標本誤差といいます。
\[\]
この式は「正規分布表のミカタ」で紹介した正規分布の標準化した統計量Zに似ていますよね。
\[Z=\frac{\bar{x}-μ}{\sqrt{\frac{σ^2}{n}}}\]
※\(σ\)は母標準偏差、\(σ^2\)は母分散をあらわします。
\(σ^2⇒V\)とすれば同じ式になります。
\[\]
「正規分布表のミカタ」では分布のばらつき具合に対する、平均の評価をしました。
その際に正規分布表を使いました。
\[\]
今回のt分布についても同様に、正規分布表が使いたいのですが・・・
(。´・ω・)?
正規分布表は使えません。
t表 というものを使います。
\[\]
②なぜ正規分布表は使えないのか
t分布の統計量tも、正規分布の統計量Zもほぼ同じ形なのに、なぜ正規分布表が使えないのでしょうか?
それは「母分散≠不偏分散」だからです。

\[\]
もし、t分布でもサンプル数\(n→∞\)となる条件であれば、「不偏分散≒母分散」となります。
しかし、サンプル数\(n\)が少ない場合(≠∞)は、標本の抽出の「不確かさ」を考慮する必要があります。
\[\]
そのため、母分散がわかっている場合の正規分布の統計量\(Z=\frac{\bar{x}-μ}{\sqrt{\frac{σ^2}{n}}}\) と、
母分散が不明な時の統計量\(t= \frac{\bar{x}-μ}{\sqrt{\frac{V}{n}}}\) は別物として考えます。
\[\]
③標準偏化された正規分布との違い
標準化された正規分布の統計量Zとt分布の統計量tは異なるといわれても、形は似ているし・・・いったい何がどう違うのでしょうか?
(。´・ω・)?
統計量tの形を変形させて意味を理解してみましょう。
そのために統計量\(t\) を式変形させてみます。
\[t= \frac{\bar{x}-μ}{\sqrt{\frac{V}{n}}}\]
\[t= \frac{\bar{x}-μ}{\sqrt{\frac{V}{n}}・\sqrt{\frac{σ^2}{V}}・\sqrt{\frac{V}{σ^2}}}\]
\[=\frac{\bar{x}-μ}{\sqrt{\frac{σ^2}{n}}}÷\sqrt{\frac{V}{σ^2}}\]
ここで、不偏分散 \(V=\frac{S}{n-1} (=\frac{平方和}{自由度})\) なので、
\[=\frac{\bar{x}-μ}{\sqrt{\frac{σ^2}{n}}}÷\sqrt{\frac{V}{σ^2}}\]
\[=\frac{\bar{x}-μ}{\sqrt{\frac{σ^2}{n}}}÷\sqrt{\frac{S}{(n-1)・σ^2}}\]
さらに、「\(χ^2カイ二乗分布とは\)」より、\(χ^2=\frac{S}{σ^2}\) なので、
\[=\frac{\bar{x}-μ}{\sqrt{\frac{σ^2}{n}}}÷\sqrt{\frac{S}{(n-1)・σ^2}}\]
\[=\frac{\bar{x}-μ}{\sqrt{\frac{σ^2}{n}}}÷\sqrt{\frac{χ^2}{n-1}}\]
割り算の左側の項は、正規分布の統計量Zを意味するので、
\[t=\frac{\bar{x}-μ}{\sqrt{\frac{σ^2}{n}}}÷\sqrt{\frac{χ^2}{n-1}}\]
\[t=\frac{Z}{\sqrt{\frac{χ^2}{n-1}}} =\frac{標準化した統計量Z}{\sqrt{\frac{χ^2の統計量}{自由度}}}\]
この時の確率分布を自由度\(n-1\)の t分布 といいます。

\[\]
最終的な式の形をみると、正規分布の統計量Zを\(\sqrt{\frac{χ^2の統計量}{自由度}}\) で割り算していることから、統計量t≠統計量Zということがわかりますね。
\[\]
④t分布のグラフ
t分布の統計量は、
\[t=\frac{\bar{x}-μ}{\sqrt{\frac{V}{n}}}=\frac{Z}{\sqrt{\frac{χ^2}{n-1}}} =\frac{標準化した統計量Z}{\sqrt{\frac{χ^2の統計量}{自由度}}}\]
この式からt分布を図であらわすと、下のようになります。

\(χ^2\)カイ二乗分布やF分布と違って、左右対称な形なのがわかりますね。
また、サンプル数\(n\)を増やすと、正規分布に近づくこともわかります。
(∪・ω・)ゞフムフム*
\[\]
⑤二標本のt分布
\(χ^2\)カイ二乗分布では、母集団と標本の分散を比較し、
F分布では同じ母集団から二つの標本を抽出した際の分散を評価しました。
\[\]
では、t分布では何ができるのでしょうか?
(。´・ω・)?
t分布では二つの標本の平均の差を比較することができます。
ばらつきを評価した \(χ^2\)カイ二乗分布 やF分布とは異なります。
では平均の差を比較する場合について、いくつかのケースで考えていきましょう。
\[\]
1.二つの母分散が既知の場合
イメージとしては、下図を参考にしてください。
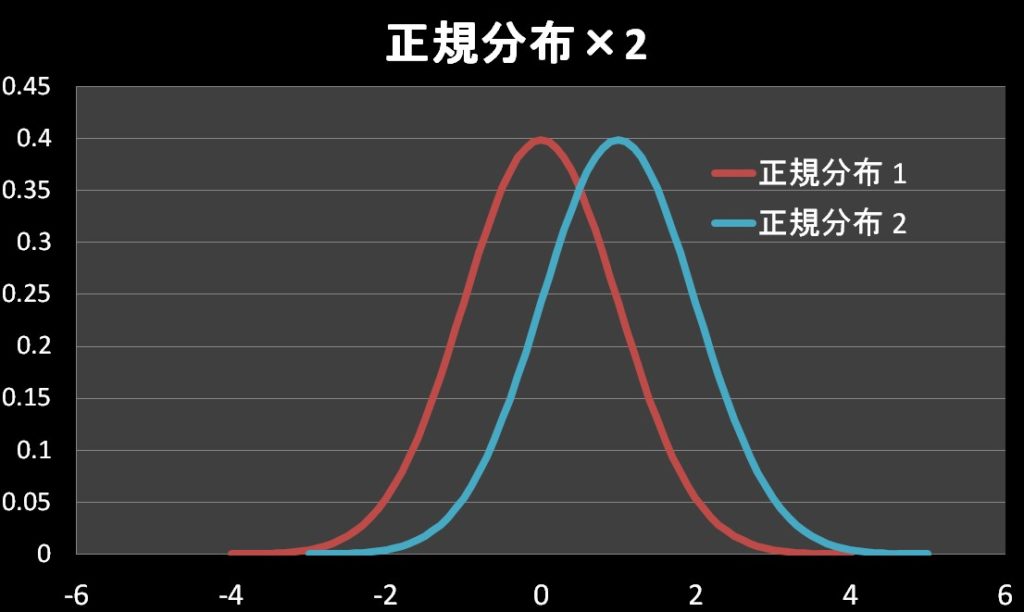
※二つの母分散がわかっているので、t分布ではないです。
この二つの独立した正規分布の違いを評価したいので、とりあえず統計量Zを引き算してみましょう。
\[Z’=Z_1-Z_2=\frac{\bar{x_1}-μ_1}{\sqrt{\frac{σ_1^2}{n_1}}}-\frac{\bar{x_2}-μ_2}{\sqrt{\frac{σ_2^2}{n_2}}}\]
※\(\bar{x_1},\bar{x_2}\)は標本の平均、\(μ_1,μ_2\)は母集団の平均、\(n_1,n_2\)はそれぞれのサンプル数をあらわします。
もう少し式を変形させて、
\[Z’=\frac{\bar{x_1}-μ_1}{\sqrt{\frac{σ_1^2}{n_1}}}-\frac{\bar{x_2}-μ_2}{\sqrt{\frac{σ_2^2}{n_2}}}\]
\[=\frac{(\bar{x_1}-μ_1)-(\bar{x_2}-μ_2)}{\sqrt{\frac{σ_1^2}{n_1}+\frac{σ_2^2}{n_2}}}\]
\[=\frac{(\bar{x_1}-\bar{x_2})-(μ_1-μ_2)}{\sqrt{\frac{σ_1^2}{n_1}+\frac{σ_2^2}{n_2}}}\]
これが、二つの標本の母分散が既知の合の統計量Z’となります。
\(σ_1^2,σ_2^2\)ともに独立した分散のため共分散の項はでません。
サラッと説明してしまいましたが、式変形で変なところがあります。
それは、「分母の足し算」です。
\[\]
普通の分数の計算では、分母が同じ値になるように掛け算をします。
しかし、正規分布に従う確率変数は、「独立な二つ以上の正規確率変数の和及び差は正規確率変数である」という定義があります。
簡単に言うと、「二つ以上の正規分布の和や差は正規分布」ってことになります。
\[\]
重要なのは分子の「平均値」は「和なら和、差なら差」なのですが、分母の「ばらつき」は「和でも差でも和」ということです。
少し不思議な気もしますが、ばらつきは加算されると考えるとわかりやすいのではないでしょうか。
\[\]
また、この二標本の統計量\(Z’\)は、母分散が既知であるため、t表は使いません。
( ´・ω・)ノ t表使わないなら意味ないじゃん
\[\]
そこで、次の場合を考えます。
2.二つの母分散は未知だが、等しいことがわかっている場合
この場合は、先ほど考えた母分散が、\(σ_1^2=σ_2^2=σ^2\) と置き換えられるので、
\[Z”=\frac{(\bar{x_1}-\bar{x_2})-(μ_1-μ_2)}{\sqrt{\frac{σ_1^2}{n_1}+\frac{σ_2^2}{n_2}}}=\frac{(\bar{x_1}-\bar{x_2})-(μ_1-μ_2)}{\sqrt{(\frac{1}{n_1}+\frac{1}{n_2})・σ^2}}\]
\[\]
・・・(。´・ω・)? で?
はい、ここでやっとt分布が登場します。
\(t=\frac{Z}{\sqrt{\frac{V}{σ^2}}}\) でしたから、
上記の\(Z”\) を\(\sqrt{\frac{V}{σ^2}}\) で割り算してみましょう。すると、
\[t=Z”÷\sqrt{\frac{V}{σ^2}} = \frac{(\bar{x_1}-\bar{x_2})-(μ_1-μ_2)}{\sqrt{(\frac{1}{n_1}+\frac{1}{n_2})・σ^2}} ÷\sqrt{\frac{V}{σ^2}}\]
\[=\frac{(\bar{x_1}-\bar{x_2})-(μ_1-μ_2)}{\sqrt{(\frac{1}{n_1}+\frac{1}{n_2})・V}}\]
このように式変形することで、二標本のt統計量を設定することができました。
これは、二つの標本に対し「母分散が同じであれば、母分散の値がわからず、サンプル数が異なっていても、t分布で標本間の平均値の違いを評価できる」ことを意味します。
少し回りくどい言い方ですが、そんなもんなんだって感じで理解しておきましょう。
\[\]
まとめ
①t分布は標準化した正規分布の統計量Zの\(σ^2⇒V\) に対応
②「不偏分散≒母分散」だから、t分布ではt表を使う
③統計量tは、正規分布の統計量Zを\(\sqrt{\frac{χ^2の統計量}{自由度}}\) で割り算
④t分布でもサンプル数\(n\)を増やすと正規分布に近づく
⑤母分散が同じなら、二つの標本の平均の違いはt分布で評価可能
\[\]
ここまでは、正規分布、\(χ^2\)カイ二乗分布、F分布、t分布と統計量について勉強してきました。
次回の検定ではこのような統計量を使って、検定・推定していく際の心構えについて勉強していきましょう!















[…] ※記事「t分布とは」をご参考ください […]
[…] 次回はt分布について勉強していきましょう! […]