直交配列実験とは 2 2水準

公開日2022年1月29日 最終更新日 2022年4月10日
みなさんこんにちは、michiです。
前回に引き続き、今回も直交表について学んでいきます。
今回は直交表を使った2水準系実験のやり方について学んでいきます。
今回の記事はかなり長めです。(;´・ω・)
キーワード:「直交配列表」

目次
実施手順
2水準系直交配列実験は、次の手順で行います。
- ①取り上げる交互作用の決定
- ②割り付け
- ③実験の実施
- ④計算補助表の作成
- ⑤平方和と自由度の計算
- ⑥分散分析の実施
- ⑦データの構造式の確認
- ⑧最適条件における母平均の推定
- ⑨母平均の差の推定
- ⑩最適水準におけるデータの予測
\[\]
結構やること多いですね。
(;´・ω・)
①~⑧は理解しておきましょう。
それでは、ひとつずつ解説していきます。
\[\]
①取り上げる交互作用の決定
今回は、2水準の因子A、因子B、因子C、因子Dと交互作用A×B、交互作用A×Cがある場合で考えてみます。
データ数から考えて、列番は7つあれば良さそうです。
(主効果 4因子 と 交互作用 2因子)
なので、\(L_8(2^7)\)直交配列表を使います。
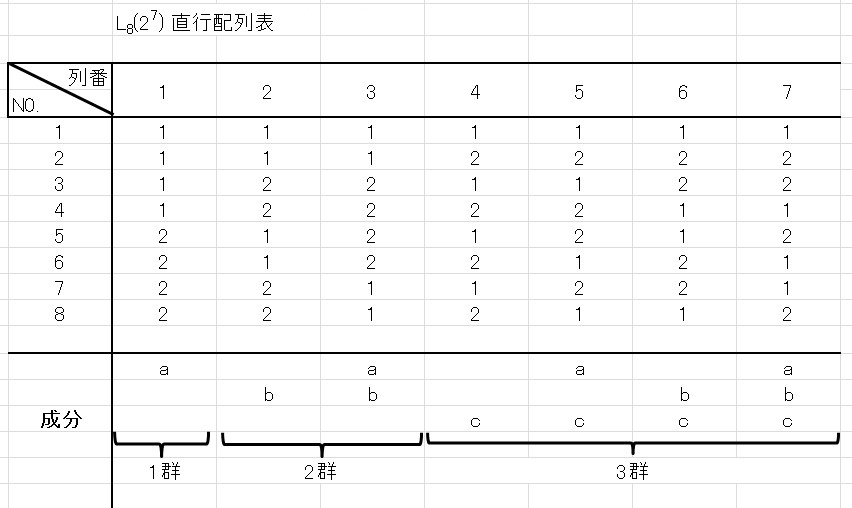
\[\]
通常、2水準系の直交配列実験では、2因子の交互作用までを対象とします。
3因子の交互作用A×B×Cやそれ以上の因子の交互作用を考えません。
3因子以上の交互作用は、実践的にも取り上げることがほとんどないためです。
\[\]
②割り付け
割り付けの方法は 前回 学びました。
今回は次のように割り付けを行いました。

\[\]
まとめると、次のようになります。
- 列番[ 1 ]が 因子A
- 列番[ 2 ]が 因子B
- 列番[ 3 ]が 交互作用A×B
- 列番[ 4 ]が 因子C
- 列番[ 5 ]が 交互作用A×C
- 列番[ 6 ]が 因子D
- 列番[ 7 ]が 誤差列
主効果も交互作用も自由度は 1 です。
各列の自由度もまた 1 になります。
\[\]
ここで疑問がわきます。
「列番[6]は成分がbc なので、交互作用B×Cと因子Dが交絡するのではないか?」 ということです。
しかし心配はいりません!
( ´・д・)エッ
\[\]
なぜなら「① 取り上げる交互作用の決定 」で交互作用B×Cは考えないことにしているためです。
そのため列番[6]に成分bc の因子Dを割り付けることができます。
※交互作用B×Cが考えられる場合は、割り付けてはいけません!
( ゚д゚)ハッ!
\[\]
③実験の実施
「②割り付け」を基に計8回の実験を行います。
各実験の水準は、直交配列表を横に読んで決めます。
(。´・ω・)?
例えば、3番目の実験では因子Aと因子Cは水準1で、因子Bと因子Dは水準2で行います。

この時、交互作用を割り付けた列番と誤差の列番は気にしなくて良いです。
\[\]
合計で実験を8回も行うなんて、多い!と感じますよね。
(o´・ω・)´-ω-)ウン
\[\]
しかし、要因配置実験で行おうとすると、「因子Aの水準数×因子Bの水準数×…」⇒16回実験する必要があります。
半分の実験回数です!
この実験回数の差は、因子の数が増えるとどんどん大きくなります。
部分配置実験 では、不必要な交互作用を無視することで、少ない実験回数で済ませることが可能となります。
\[\]
④計算補助表の作成
8通りの実験結果が下図の「データ」のように得られたとします。

実験No.1の結果は「5」、実験No.7の結果は「16」です。
\[\]
次に各列番ごとに第1水準、第2水準の合計と平均を求めます。

例えば、列番3の第1水準の合計は 46 です。
計算方法は、列番3が第1水準で実験する「実験No.1」 「実験No.2」 「実験No.7」 「実験No.8」 の4回のデータを合計して求めます。
5+8+16+17 = 46 となるわけです。

\[\]
交互作用がある場合は、二元表を作成します。
今回は交互作用A×Bと、交互作用A×Cの二元表を作成します。

アルファベットの横の数字が水準を表します。
水準の組み合わせ A2B1 の 23 という結果は、 「実験No.5」 「実験No.6」の2回のデータの和から求めます。
12+11 = 23 となるわけです。

\[\]
列番4に割り付けた因子Cは水準1と水準2が交互に出てきます。
AC二元表の A1C2 の 16 という結果は、 「実験No.2」 「実験No.4」の2回のデータの和(8+8)から求めます。
\[\]
⑤平方和と自由度の計算
①修正項の計算
要因配置実験と同じように、修正項CTを計算します。
今回はデータの合計 \(T=88\) なので、
\[CT=\frac{T^2}{N}=\frac{88^2}{8}=968\]
となります。
\(N=8\) というのは、総データ数のことです。
\(L_8(2^7)\)直交配列表 では、8回実験を行うので \(N=8\) となります。
\[\]
②各列ごとの平方和(列平方和)を求める
第 \(k\) 列の平方和は次の式で計算できます。
\[S_{[k]}=\frac{{T_{[k]1}}^2}{N/2}+ \frac{{T_{[k]2}}^2}{N/2}-CT \]
第1項 \( \frac{{T_{[k]1}}^2}{N/2} \) は、各列における第1水準の合計の2乗を、「(総データ数 \(N\))/2」で割った値になります。
「 (総データ数 \(N\))/2」 の「2」は2水準だからです。
つまり、 (総データ数 \(N\))/2 =第1水準のデータ数 を意味します。
\[\]
第2項\( \frac{{T_{[k]2}}^2}{N/2} \) についても同様に考えて、第2水準の合計の2乗を第2水準のデータ数で割った値となります。
最後に修正項を引いて、 第 \(k\) 列の平方和は計算完了です。
2水準系の列平方和の計算は、次の式 でも 計算できます。
\[S_{[k]}=\frac{{T_{[k]1}}^2}{N/2}+ \frac{{T_{[k]2}}^2}{N/2}-CT \qquad ⇒ \qquad \frac{(T_{[k]1}- T_{[k]2} )^2}{N} \]
\[\]
③列平方和のまとめ
列平方和を計算し、表にまとめます。
すると、次の表のようになります。

例えば、列番7の列平方和(\(S_{[k]}\)) の計算は次のようになります。
\[S_{[k]}=\frac{{T_{[k]1}}^2}{N/2}+ \frac{{T_{[k]2}}^2}{N/2}-CT\]
\[= \frac{40^2}{8/2}+ \frac{48^2}{8/2}-968 \]
\[=\frac{1600}{4}+\frac{2304}{4}-968\]
\[=400+576-968 \qquad= 8\]
または、
\[S_{[k]}= \frac{(T_{[k]1}- T_{[k]2} )^2}{N} \]
\[S_{[k]}= \frac{(40- 48 )^2}{8} \]
\[S_{[k]}= \frac{64}{8} \qquad =8 \]
この表をもとに、分散分析表を作っていきます。
╭( ・ㅂ・)و̑ グッ
\[\]
⑥分散分析の実施
列平方和の表を参考に、分散分析表を作成します。
分散分析表は次のようになります。

…あれ?自由度がのきなみ「1」ですね。
(。´・ω・)?
\[\]
なぜこのようになるのかというと、各列の水準数は「2」だからです。
自由度は 「水準数-1=1」となります。
¥[¥]
誤差の平均平方が「8」なので、各因子毎の\(F_0\) 値を求めると、次の表のようになります。
※因子毎の\(F_0\)値は、因子毎の平均平方を誤差の平均平方で割ることで求めます。

このとき、目安として \(F_0\) 値 が2以下のものはプールします。(プーリング)
\(F_0\) 値 の小さなものは 誤差 とみなすわけです。
ただし、交互作用をプールしない時は、その主効果 \(F_0\) 値が2以下であっても、主効果 \(F_0\) 値プールしません。
“φ(・ω・。)フムフム…
\[\]
先ほどの表を確認すると、「因子C、因子D、交互作用A×B、交互作用
A×C」の \(F_0\) 値 が2以下となるので、誤差にプールし計算をしなおします。
その結果は次の表となります。


因子A、因子Bともに\(F_0\)値はF境界値よりも大きいです。
因子Aと因子Bは結果へ影響をあたえ、因子Cや因子D、交互作用A×Bと交互作用A×Cは結果へ影響を与えないと考えられます。
\[\]
⑦データの構造式の確認
データの構造式は、全体平均にそれぞれの水準効果を加えたものになります。
データの構造式を確認することで、最適水準における点推定値を求めることができます。
\[\]
今回の例で考えると、データの構造式は次のようになります。
※ハット記号が小さいのはご愛嬌ということで…
\[\hat{\mu}(ABCD)=\widehat{\mu+a+b+c+d+(ab)+(ac)}\]
\(\mu\) は全体平均のことです。
\[\]
因子Aの効果で、全体平均より a だけ上昇(下降)します。
同様に因子B、因子C、因子Dによる効果は b, c, d と書いています。
交互作用による効果は A×Bは\((ab)\)、 A×Cは\((ac)\) と書いています。
全体平均 \(\mu\) に各因子と交互作用が作用していることを、データの構造式では表しています。
\[\]
データの構造式を分解しみましょう!
\[ \hat{\mu}(ABCD)= \widehat{\mu+a+b+c+d+(ab)+(ac)}\]
\[↓\]
\[\widehat{\mu+a+b+(ab)} \qquad +\widehat{\mu+a+c+(ac)} \qquad +\widehat{\mu+d}\qquad -\hat{\mu} \qquad -\widehat{\mu+a}\]
\[\]
全体平均\(\hat{\mu}\) を 1回 、因子Aの効果 \(\widehat{\mu+a} \) を1回引いています。
(。´・ω・)?
理由は、各因子の効果に分解するときは、「全体平均と因子による和で取り出されるため」です。
因子による効果のみを取り出すことはできません。
例えば、因子Dによる効果を分離するときは「 \(\widehat{\mu+d}\) 」と表しています。
\[\]
因子Aでは交互作用が二つ(A×B、A×C)あるため、データの構造式を分解するときは、 因子Aの効果 \(\widehat{\mu+a} \) を1回引く必要があります。
\[\]
⑧最適条件における母平均の推定
データの構造式が決まったら、次は最適水準を決めます。
「⑦ データの構造式の確認 」では、データの構造式を分解しました。
しかし「⑥ 分散分析の実施 」の結果では、効果があるのは因子Aと因子Bのみでした。
プーリングした因子や交互作用を消すと、データの構造式は次のようになります。
\[ \hat{\mu}(ABCD)= \widehat{\mu+a+b+c+d+(ab)+(ac)}\]
\[↓\]
\[\widehat{\mu+a} \qquad +\widehat{\mu+b} \qquad -\hat{\mu} \]
\[\]
交互作用A×B(ab)が消えています!
Σ(・ω・ノ)ノ!
「AB二元表の最適水準」=「水準Aの最適水準 かつ Bの最適水準」だからです。
つまり、因子A、因子Bの最適水準がAB二元表の最適水準と同じになります。
最適水準を決めるのに、交互作用は無視して良いわけです。
(´・д・`)フーン
\[\]
列平方和の表を見てみましょう。

列番1に因子Aを、列番2に因子Bを割り付けました。
列番1と列番2のいずれも「第2水準」が最適水準であることがわかります。
(数値が大きいほどよいとしています)
最適水準における母平均の推定値は「\(A_2B_2\)」となります。
\[\]
ちなみに、AB二元表を確認してみると…

やはり「\(A_2B_2\)」が最適水準となりますね。
「交互作用がない」とは「最適水準と二元表の値」が同じ状態を意味します。
\[\]
母平均の信頼区間は、次式より求められます。
\[\hat{\mu}(A_2B_2)\pm t(\phi_E,\alpha)\sqrt{\frac{V_E}{n_e}}\]
信頼区間の考え方は、実験計画法と同じです。
φ(❐_❐✧メモメモ
\[\]
はじめに母平均を計算すると、
\[ \hat{\mu}(A_2B_2)= \widehat{\mu+a} +\widehat{\mu+b} -\hat{\mu} \]
\[=\frac{A_2の合計値}{A_2の実験回数}+\frac{B_2の合計値}{B_2の実験回数}-\frac{全体の合計}{全体の実験回数}\]
\[=\frac{56}{4}+\frac{52}{4}-\frac{88}{8}\]
\[=14+13-11 \qquad =16\]
となります。
\[\]
有効反復係数\(n_e\) は、
\[n_e=\frac{総データ数}{1+自由度の和}\]
です。
総データ数は、今回8回の実験を行っているので、 8 となります。
自由度の和は、因子Aと因子Bの二つを考えればよく、2水準ですので、「1+1=2」となります。
よって、有効反復係数\(n_e\) は、
\[n_e=\frac{総データ数}{1+自由度の和} \qquad=\frac{8}{1+1+1} \qquad = \frac{8}{3}\]
です。
信頼率95%での区間推定を計算すると、
\[\hat{\mu}(A_2B_2)\pm t(\phi_E,\alpha)\sqrt{\frac{V_E}{n_e}}\]
\[=16\pm t(5,0.05)\sqrt{\frac{3}{8} \times 3.3}\]
\[=16 \pm 2.570 \times 1.112\]
\[=16 \pm 2.86\]
\[=13.14 , 18.86 \]
\[\]
ポイントは、最適水準における検証を実施することです。
要因配置実験では16回の実験が必要なところを、部分配置実験では8回しか行っていません。
最適な組み合わせを理論上見つけることができても、実際に最適な組み合わせで実験を行っていない可能性があります。
部分配置実験で求めた最適な組み合わせが最適なのか否か検証してみましょう!
\[\]
⑨母平均の差の推定
ここからはテキストにはない内容ですが、実践面で使えるので紹介します。
先ほどの例で引き続き考えてみましょう。
\[\]
最適水準の組み合わせは「\(A_2B_2\)」で、母平均の推定値は「16」です。
ところが、今現在の組み合わせが「\(A_1B_1\)」であったとします。
今の組み合わせ 「\(A_1B_1\)」 から最適水準 「\(A_2B_2\)」 に変更すると、どの程度効果がでるかを「母平均の差の推定」から見積もってみましょう。
これが見積もれると、水準変更の有効性を評価できます!
(σ・ω・)σソレナ
\[\]
①点推定値の差分を求める
点推定値を求めると、最適水準の組み合わせでは「 \(A_2B_2\) 」=16 となります。
組み合わせが 「\(A_1B_1\) 」の時の点推定値は「6」となります。
\[\frac{32}{4}+\frac{36}{4}-\frac{88}{8}\]
\[=8+9-11 \qquad = 6\]

※列番1が因子A、列番2が因子Bと割り付けました。
\[\]
②有効反復係数を求める
有効反復係数\(n_e\) を求めます。
先ほどは「田口の式」で計算しました。
伊奈の式から計算すると、
\[\frac{1}{n_e}=\frac{1}{4}+ \frac{1}{4}- \frac{1}{8} =\frac{3}{8}\]
とやはり同じ結果になります。
伊奈の式から計算した理由は、気分です。
ヾ(-д-;)ぉぃぉぃ
\[\]
③信頼率をする95%で区間推定をする
それでは最適水準の組み合わせと任意の組み合わせの母平均の差を推定します。
計算式は
\[\hat{\mu}(A_2B_2)-\hat{\mu}(A_1B_1) \]
です。
\[ \hat{\mu}(A_2B_2)-\hat{\mu}(A_1B_1) =16-6 =10 \]
\[\]
次に、信頼率95%で区間推定を行うと、計算式は以下のようになります。
\[ (\hat{\mu}(A_2B_2)-\hat{\mu}(A_1B_1)) \pm t(\phi_E,\alpha)\sqrt{\frac{2}{n_e} V_E } \]
\[=10 \pm t(5,0.05)\sqrt{2\times \frac{3}{8} \times 3.3 } \]
\[=10 \pm 2.570 \times 1.573\]
\[=10 \pm 4.04 \qquad \]
\[= 5.96,14.04\]
となります。
\[\]
⑩最適水準におけるデータの予測
最後に最適水準におけるデータの予測を行います。
(。´・ω・)?
今までの計算は、最適水準における母平均の点推定値、または信頼区間の幅を求めました。
そうです、あくまでも母平均です。
\[\]
実際に観測される値は、分布に幅があることから母平均からずれて観測されます。

\[\]
観測される値がどのくらいの区間に存在するかというと、母平均の信頼区間の \(\frac{V_E}{n_e}\) に \(V_E\) を加えた値となります。
式で表すと次のとおりです。
\[\hat{\mu}(ABCD)\pm t(\phi_E,\alpha)\sqrt{\left( 1+\frac{1}{n_e}\right)V_E}\]
\[\]
予測値は母平均の点推定値と同じになりますが、幅が異なります。
実際に最適水準「\(A_2B_2\)」で計算してみると…
\[\hat{\mu}(A_2B_2)\pm t(\phi_E,\alpha)\sqrt{\left( 1+\frac{1}{n_e}\right)V_E}\]
\[=\hat{\mu}(A_2B_2)\pm t(5,0.05)\sqrt{\left( 1+\frac{3}{8}\right)\times 3.3}\]
\[=16 \pm 2.570 \times 2.130\]
\[=16 \pm 5.47\]
\[=10.53, 21.47\]
\[\]
最適水準「\(A_2B_2\)」における信頼率95%での母平均の推定値が「13.14, 18.86」 でした。
観測される予測値は、母平均の推定値よりも広い領域にあることを意味します。
\[\]
考え方は、「母平均が信頼区間の端に近づくと、分布の幅分はみ出てしまう」です。
予測区間は母平均の位置が信頼区間の端に来た時に、測定点が観測される領域を意味します。


\[\]
まとめ
①2水準の直交配列実験では、3因子以上の交互作用を考えない
②割り付け方法は、 前回 の記事を参考にする。
③各実験の水準は、直交配列表を横に読んで決める
④計算補助表は、実験データを列番毎にまとめる(または二元表)
⑤列ごとに列平方和を計算する
⑥誤差に入れれそうな因子や交互作用は、誤差にプーリング
⑦データの構造式から推定値の計算式を導く
⑧母平均の推定は \(\hat{\mu}(ABCD)\pm t(\phi_E,\alpha)\sqrt{\frac{V_E}{n_e}}\)
⑨母平均の差 を推定すれば、水準を変えるべきか判断できる
⑩予測値 ≠ 推定値
\[\]
今回はかなり長めの記事でした。
直交配列表を使った実験は、因子の数が増えるほど有効です。
実践で使ってみましょう!
\[\]
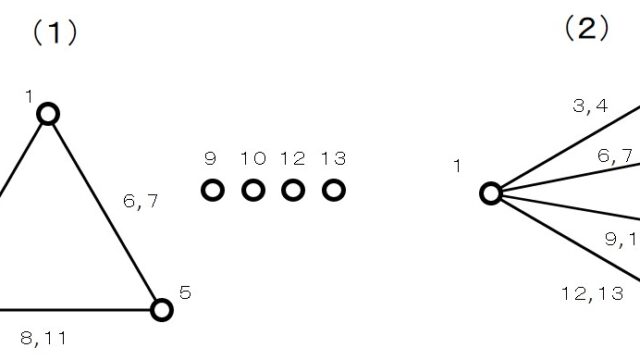


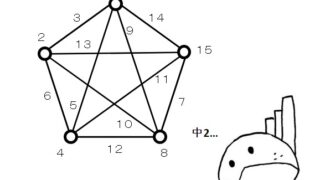










[…] 前回と異なり、自由度が1ではありません。 […]
[…] 前回(直交配列実験とは 2 2水準)、前々回(直交配列実験とは 3 3水準)の記事で学んだ、2水準法と3水準法についてまずは復習です。 […]