検出力、p値　とは

公開日2021年10月31日 　最終更新日 2021年11月28日

みなさんこんにちは、michiです。

今回は検出力とp値について勉強します。

検出力とp値について学ぶ前に、第一種の誤りと第二種の誤りの復習をします。

記事「検定とは」の復習も兼ねて、学んでいきましょう！

キーワード：「検出力」「p値」

①第一種の誤り　とは

第一種の誤りとは、本当は帰無仮説\(H_0\) が成り立っているにもかかわらず、これを棄却する誤りのことです。

専門用語のおさらいです。

• 帰無仮説\(H_0\)：成り立っていないと思われる仮説（無に帰すことが目的の仮説）
• 対立仮説\(H_1\)：成り立っていると思われる仮説（主張したい仮説）

\[\]

正規分布に従う集団の平均値に対し、有意水準5%の片側検定を考えてみます。

サンプリングを行い検定統計量を求めた結果、下図のようになったとします。

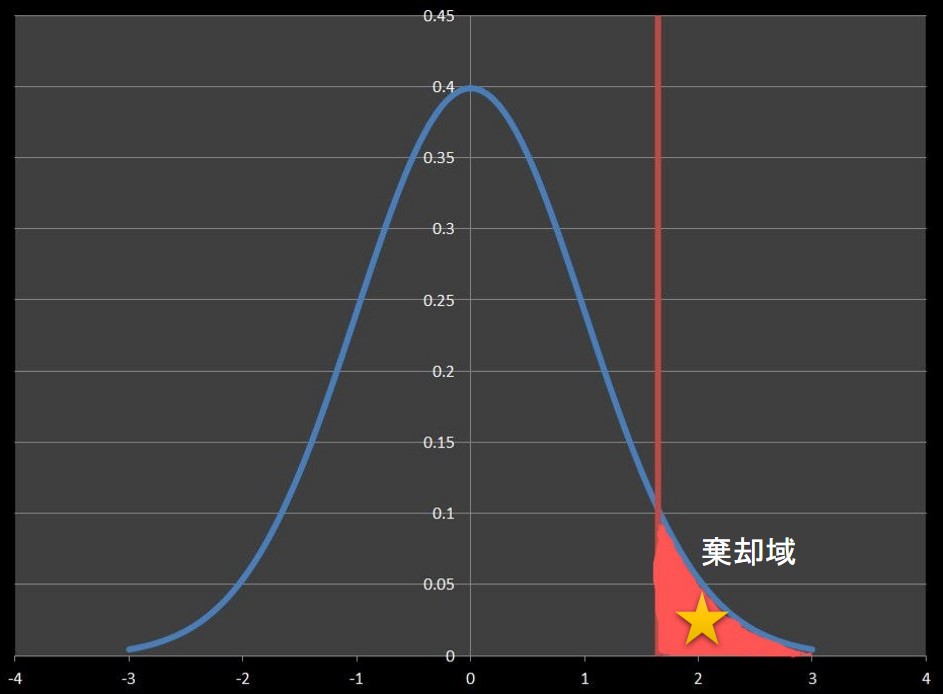
検定統計量★は棄却域にあるため帰無仮説を棄却し、「平均値は変化した」と判断します。

φ(･ω･ )ﾌﾑﾌﾑ…

\[\]

ここで考えてほしいことは、有意水準の意味です。

有意水準を5%に設定したということは、めったに起きないこと（5%）が起きた時に、「珍しいことが起きた！」と考えるのではなく、違う分布に属すると考ます。

違う分布に属するとは、帰無仮説を棄却することを意味します。

しかし、めったに起きないこと（5%）は絶対に起きないことではありません。

有意水準5%の確率で起きてしまいます。

\[\]

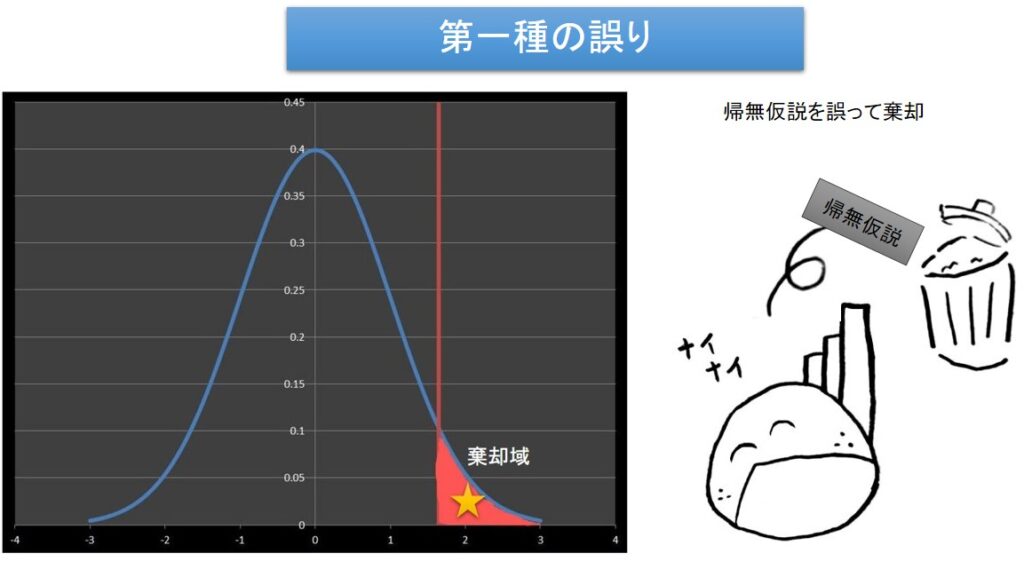
このように、めったに起きないことが起きた時に、帰無仮説が成り立っているにもかかわらず、帰無仮説を誤って棄却してしまうことを第一種の誤りと言います。

\[\]

\[\]

②第二種の誤りとは

第二種の誤りとは、本当は帰無仮説\(H_0\)が成り立っていないにもかかわらず、これを棄却しない誤りのことです。

第一種の誤りと同様に、正規分布に従う集団の平均値に対し、有意水準5%の片側検定を考えてみます。

サンプリングを行い検定統計量を求めた結果、下図のようになったとします。

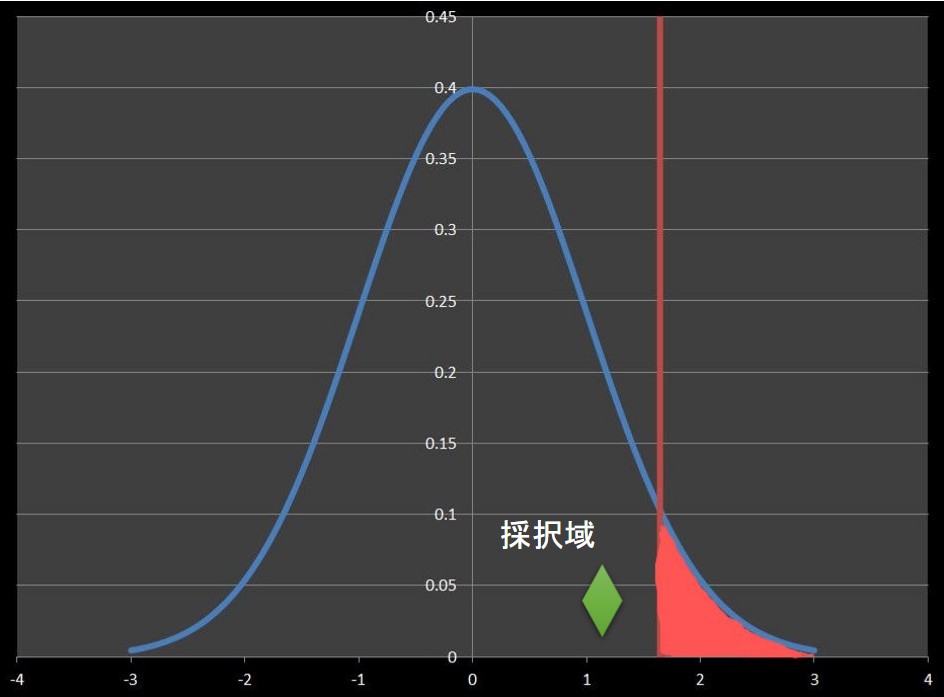
検定統計量♦は採択域にあるため、帰無仮説を採択しました。

\[\]

ところで、この図で表されている分布は何を表すのでしょうか？

(。´･ω･)?

\[\]

・・・これは帰無仮説\(H_0\) が成り立つという仮定の下での検定統計量の確率分布を表します。

そのため、任意の有意水準を設定し、検定統計量が棄却域にあれば、帰無仮説\(H_0\) の分布に属さないと判定できたわけです。

では検定統計量♦の図に、帰無仮説\(H_0\) だけではなく、対立仮説\(H_1\) の分布も描いてみます。

\[\]

帰無仮説\(H_0\) の採択域内であっても、対立仮説\(H_1\) の分布と重なっていることがわかります。

検定統計量♦は採択域にあるため、帰無仮説\(H_0\) を採用しましたが、実は対立仮説\(H_1\) の分布に属している可能性があります。

つまり、本当は帰無仮説\(H_0\) を棄却し、対立仮説\(H_1\) を採択するべきなのかもしれません。

(ﾟロﾟ; 三 ;ﾟロﾟ)

\[\]

このように、本当は帰無仮説\(H_0\) を棄却しなければならないのに、検定統計量が採択域にあるために誤って帰無仮説\(H_0\) を採択することを第二種の誤りといいます。

\[\]

第一種の誤りは有意水準を用いてその検定の精度を指定できたのに対し、第二種の誤りについては対立仮説\(H_1\) の分布次第ということがポイントになります。

\[\]

③帰無仮説\(H_0\) が採択された時の表現

第一種の誤りと第二種の誤りについて学びました。

ここでもう少し深堀してみましょう。

「帰無仮説\(H_0\) を棄却し、対立仮説\(H_1\) を採択した場合」は、有意水準を使って、判断の誤り（第一種の誤り）を設定できます。

したがって、有意水準\(\alpha\)% という条件の下で帰無仮説\(H_0\) を棄却し、対立仮説\(H_1\) を採択することができます。

表現としては「 有意水準\(\alpha\)% の下で有意ではない」、つまり「有意水準\(\alpha\)% で異なる」と言えます。

\[\]

一方、「 帰無仮説\(H_0\) を採択し、対立仮説\(H_1\) を棄却した場合 」は、先ほどと異なり判断の誤りの確率（第二種の誤り）を設定できません。

なぜなら、対立仮説\(H_1\) の分布がわからないためです。

有意水準\(\alpha\)を5%とすると、 この時の第二種の誤りをする確率\(\beta\) は0%～95% までの値をとります。

対立仮説\(H_1\) の分布がわからないので、第一種の誤りと違い、〇%の確率で同じである（帰無仮説\(H_0\) が正しい）と積極的に言えません。

したがって、 「 帰無仮説\(H_0\) を採択し、対立仮説\(H_1\) を棄却した場合 」は「差があるとは言えない」という消極的な表現となります。

※「同じである」という表現を使うには対立仮説\(H_1\) に属さないと言い切る必要があります。

第二種の誤りは0%～95%くらいの可能性があるため、言い切ることができません。

(A；´･ω･)ﾌｷﾌｷ

\[\]

④検出力とは

検出力とは「本当は帰無仮説\(H_0\) が成り立っていないときに、帰無仮説\(H_0\) を棄却する確率」のことです。

第二種の誤りを\(\beta\) とすると、検出力は\(1-\beta\) となります。

有意水準\(\alpha\) を\(5\)% とすると、\(\beta\) は\(0\)～\(95\)% までの範囲があるので、検出力は\(5\)%～\(100\)%となります。

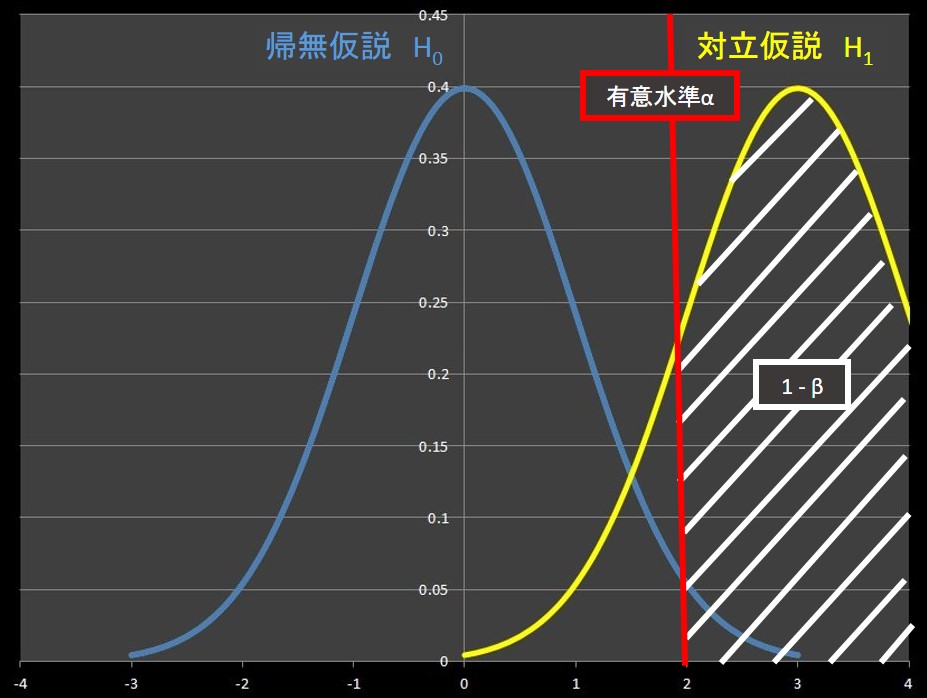
第一種の誤り、第二種の誤りとの関係を図示すると下図のようになります。

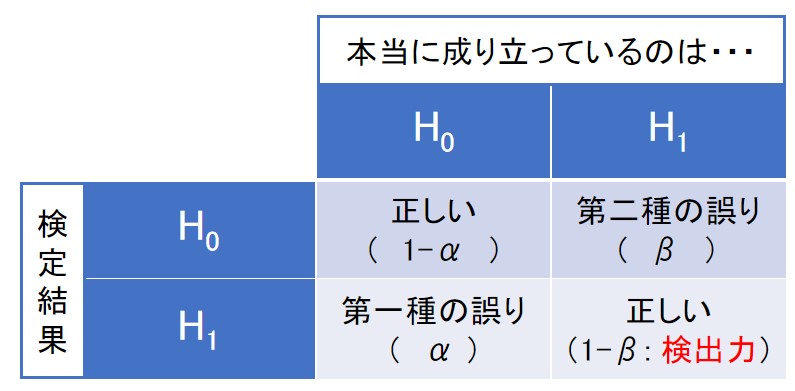
※ 帰無仮説\(H_0\) を棄却するとき、検定結果は\(H_1\) を採用することになります。

\[\]

検出力はデータ数によって変化します。（下図）

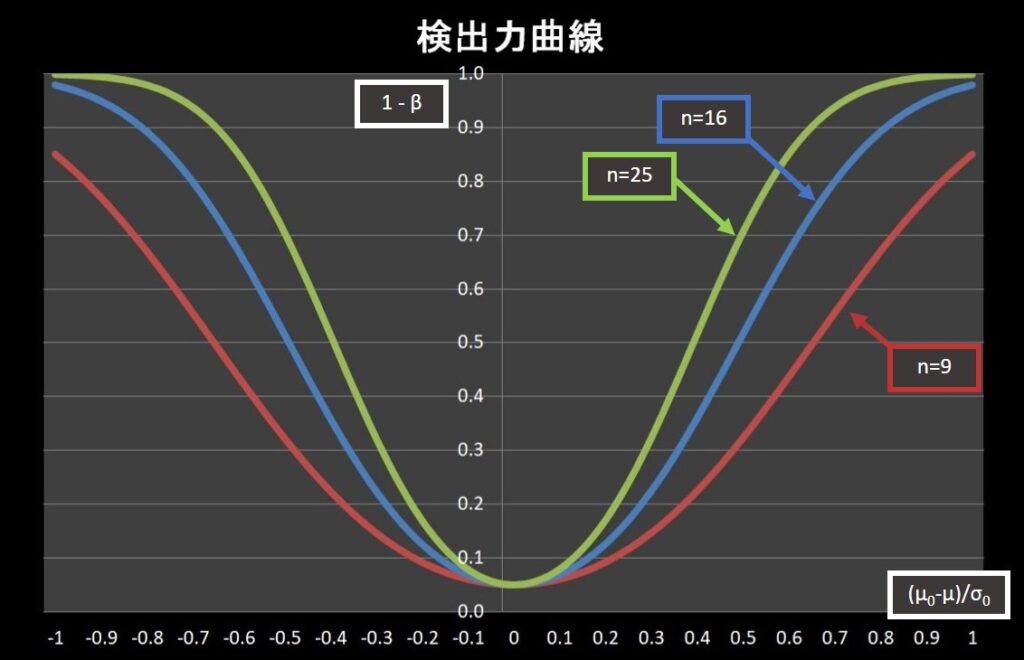
上図で表されている曲線を検出力曲線といいます。

データ数を増やすことで、検出力を上げることが可能になります。

\[\]

検出力曲線は横軸に\(\frac{\mu_0-\mu}{\sigma_0}\) 、縦軸に\(1-\beta\) があります。

\(\frac{\mu_0-\mu}{\sigma_0}\) は基準化で学んだ式です。

\(\frac{\mu_0-\mu}{\sigma_0}=0\) は、二つの分布(\(H_0\)の下での分布と\(H_1\)の下での分布)の平均値が一致する状態です。

この時の検出力は 0.05(=5%) となり、有意水準αと同じになります。

\[\]

次に、 \(\frac{\mu_0-\mu}{\sigma_0}\) を大きくした場合を考えます。

\(\frac{\mu_0-\mu}{\sigma_0}\) を大きく（小さく）すると、データ数にかかわらず検出力が上がります。

二つの分布の平均値の差が広がるので、分布の重なる部分が少なくなるためです。

\[\]

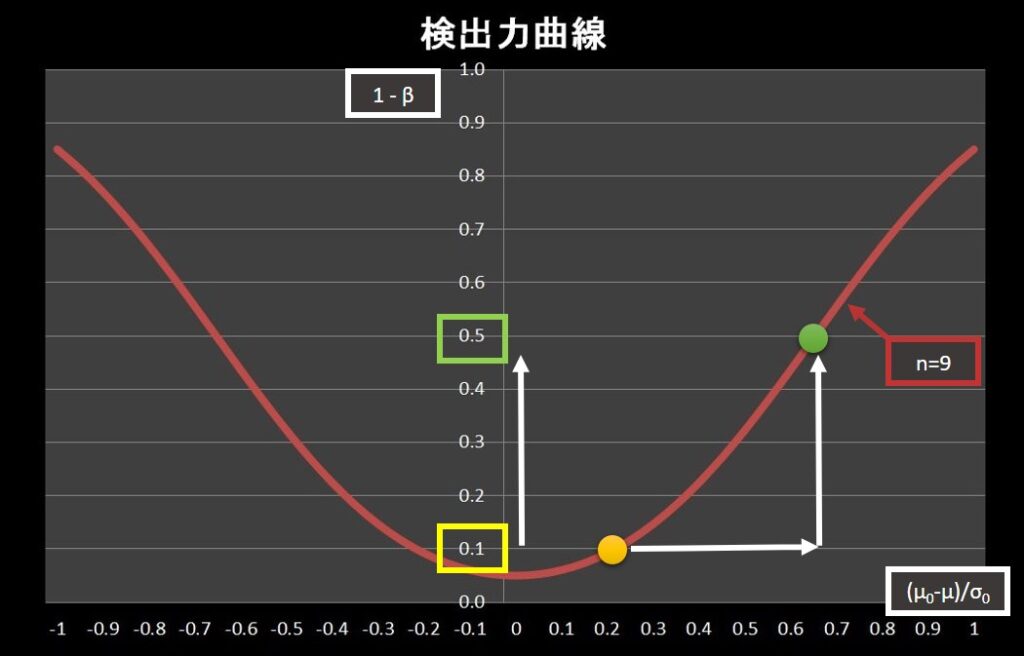
最後に \(\frac{\mu_0-\mu}{\sigma_0}=0.5\) の場合を考えます。

基準化した値が同じであるならば、データ数が多いほうが検出力が上がります。

これは、データ数が多くなることで分布の広がりが小さくなり、平均値の差は同じでも重なる部分が少なくなるためです。

\[\]

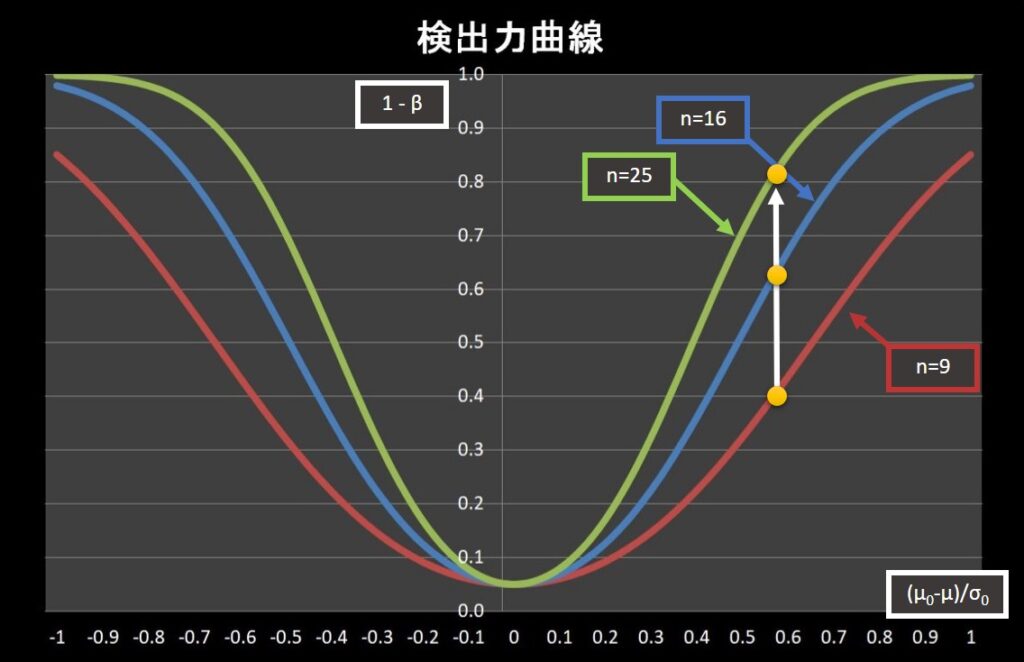
⑤検出力の計算式

平均値の検定に対し、検出力\(1-\beta\) を計算します。

• 帰無仮説\(H_0\) :\(\mu=\mu_0\)
• 対立仮説 \(H_1\) :\(\mu \neq \mu_0\)
• 帰無仮説\(H_0\) の下での\(\bar{x}\) の分布の平均値: \(\mu_0\)
• 対立仮説\(H_1\) の下での\(\bar{x}\) の分布の平均値: \(\mu\)

\[\]

検出力の計算式は次のようになります。

\[1-\beta=Pr \left\{ \bar{x}\leq \mu_{0}-1.960 \sqrt{\frac{\sigma_{0}^2}{n}} \right\}+ Pr \left\{ \bar{x}\geq \mu_{0}+1.960 \sqrt{\frac{\sigma_{0}^2}{n}} \right\} \]

\[\]

Pr はある事象Aが起こる確からしさを表したものです。

Pr{A} と書くと、Aが起きる確率を表します。

絶対に事象Aが確実に起きる場合は Pr{A}=1 となり、50%の確率なら Pr{A}=0.5 となります。

\[\]

さて、\(\pm 1.960 \sqrt{\frac{\sigma_{0}^2}{n}} \)が何かというと、これは棄却位置と採択域の境界線になります。

※数字の詳細は、記事「正規分布表のミカタ」をご参照願います。

検出力\(1-\beta\) は帰無仮説\(H_0\) の下で\(\bar{x}\) が棄却域にある確率を表します。

※上図では、わかりやすくするために\(\mu > \mu_o\) のみを図示しています。

\[\]

検出力の式では棄却域が二つあることがわかります。

pr｛〇 〇 ｝が二つありますよね。

(。´･ω･)?

これは対立仮説\(H_1\) が「\(\mu \neq \mu_0\)」と両側検定のため、棄却域が採択域をまたがって両サイドにあるためです。

\[\]

検出力の式を変形していきます。

\[1-\beta=Pr \left\{ \bar{x}\leq \mu_{0}-1.960 \sqrt{\frac{\sigma_{0}^2}{n}} \right\}+ Pr \left\{ \bar{x}\geq \mu_{0}+1.960 \sqrt{\frac{\sigma_{0}^2}{n}} \right\} \]

\[1-\beta=Pr \left\{ \frac{\bar{x}-\mu}{ \sqrt{\frac{\sigma_{0}^2}{n}} }\leq \frac{\mu_{0}-\mu}{ \sqrt{\frac{\sigma_{0}^2}{n}} }-1.960 \right\} + Pr \left\{ \frac{\bar{x}-\mu}{ \sqrt{\frac{\sigma_{0}^2}{n}} }\geq \frac{\mu_{0}-\mu}{ \sqrt{\frac{\sigma_{0}^2}{n}} }+1.960 \right\} \]

\[=Pr\left\{ u \leq \sqrt{n} \times \frac{\mu_{0}-\mu}{\sqrt{ \sigma_{0}^2 }} -1.960 \right\}+ Pr\left\{ u \geq \sqrt{n} \times \frac{\mu_{0}-\mu}{\sqrt{ \sigma_{0}^2 }} +1.960 \right\} \]

ここで、

\[u= \frac{\bar{x}-\mu}{ \sqrt{\frac{\sigma_{0}^2}{n}}} \]

としました。

\(\mu\) は対立仮説\(H_1\) の下での\(\bar{x}\) の分布の平均値を表すので、\(u\) はその基準化した値になります。

\(\frac{\mu_0-\mu}{\sqrt{\sigma_{0}^2}} =0.5\) とすると、検出力は

\[=Pr\left\{ u \leq \sqrt{n} \times \frac{\mu_{0}-\mu}{\sqrt{ \sigma_{0}^2 }} -1.960 \right\}+ Pr\left\{ u \geq \sqrt{n} \times \frac{\mu_{0}-\mu}{\sqrt{ \sigma_{0}^2 }} +1.960 \right\} \]

\[=Pr\left\{ u \leq 0.5 \sqrt{n} -1.960 \right\}+ Pr\left\{ u \geq 0.5\sqrt{n} +1.960 \right\} \]

となります。

データ数\(n=9\) の場合を考えます。

第一項は、\(\sqrt{9}=3\) なので、

\[ Pr\left\{ u \leq 0.5 \sqrt{n} -1.960 \right\} \]

\[ Pr\left\{ u \leq 1.5 -1.960 \right\} \]

\[ Pr\left\{ u \leq -0.46 \right\} \qquad ⇒0.3228 \]

同様に、第二項は

\[ Pr\left\{ u \geq 0.5 \sqrt{n} +1.960 \right\} \]

\[ Pr\left\{ u \geq 1.5 +1.960 \right\} \]

\[ Pr\left\{ u \geq 3.46 \right\} \qquad ⇒0.00027 \]

となります。

確率変数（Pr{}の中身）を求め、正規分布表から確率を計算しました。

パーセント表示をすると、第一項は32.28%　第二項は0.027% になります。

\[\]

第一項と比べると第二項は無視して良いレベルと判断できます。

よって、今回は検出力の計算で第一項だけを考えていきます。

(*´･ω･)´-ω-) ぅぃ

\[\]

検出力が0.9(90%) の場合を考えると、正規分布表より確率変数\(K_p=1.282\) が求められます。

検出力は、

\[1-\beta=0.9= Pr\left\{ u \leq 0.5 \sqrt{n} -1.960 \right\} \]

確率変数に着目して、

\[0.5 \sqrt{n} -1.960 = 1.282\]

\[ 0.5 \sqrt{n} = 3.242 \]

\[\sqrt{n} =6.484\]

\[n=42.04…\]

検出力を90%にするためには、データ数\(n\) が43個以上であれば良いことになります。

(*´･ω･)´-ω-) ぅぃ

\[\]

必要なデータ数を求めるには、二つ準備が必要です。

• 検出力の設定
• 基準化した\(\frac{\mu_0-\mu}{\sqrt{\sigma_{0}^2}}\) の確率変数

検出力は分析者が設定できますが、\(\frac{\mu_0-\mu}{\sqrt{\sigma_{0}^2}}\) は「○○の場合」という条件を仮定していることに気をつけてください。

\[\]

⑥P値とは

P値とは、計算された検定統計量よりも極端な値が得られる確率のことです。

片側検定でp値が10%、有意水準が5%の状態を図示すると下図のようになります。

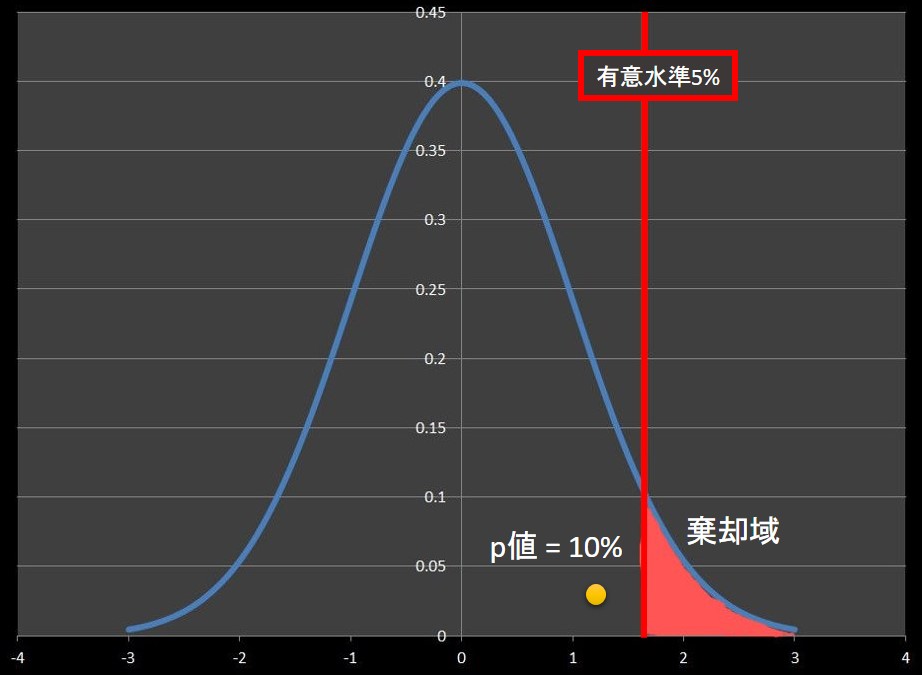
検定統計量は採択域にあるので、この検定結果は「有意ではない」となります。

この時、「P値 ＞ 有意水準」となります。

\[\]

片側検定でp値が3%、有意水準が5%の状態を図示すると下図のようになります。

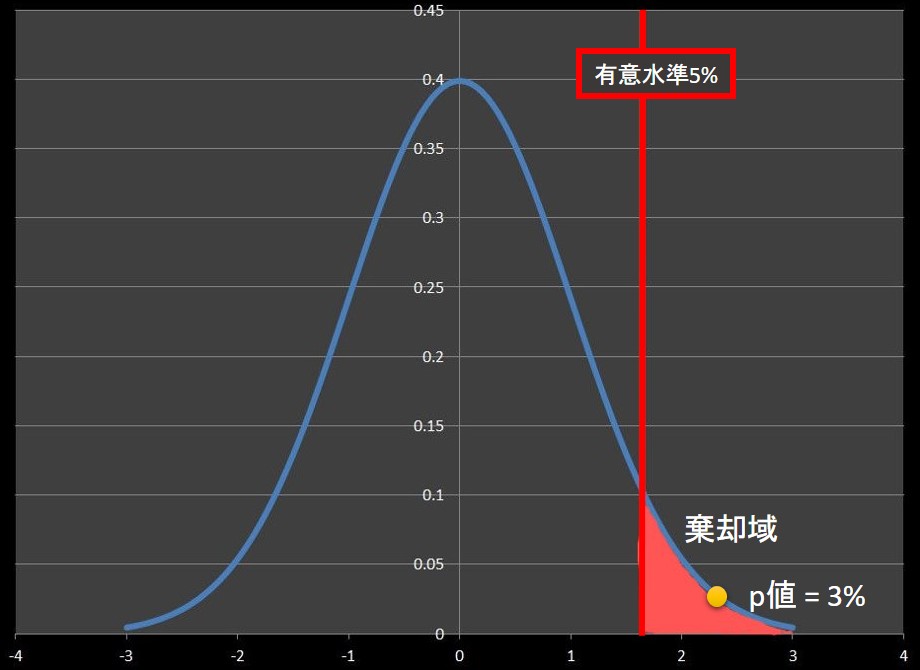
検定統計量は棄却域にあるため、検定結果は「有意」となります（帰無仮説は棄却）。

この時、「P値 ＜ 有意水準」となります。

\[\]

では、両側検定の場合はどうなるのでしょうか？

両側検定の場合は棄却域が両側に出てきます。

\[\]

検定結果に対するP値と有意水準の関係に変化はありません。

ただし、P値は2倍になります。

(。´･ω･)?

P値は 「計算された検定統計量よりも極端な値が得られる確率」 です。

両側検定の場合は、考えなくてはならない極端な値が大きすぎる場合と小さすぎる場合の2パターンがあるので、2倍になります。

\[\]

最後にP値の注意点です。

「P値を求めてから有意水準を決めない！」　です。

((´-ω-｀;)ゞﾎﾟﾘﾎﾟﾘ

検定は有意水準という判断基準を求めてから、検定統計量を求めます。

P値は検定統計量から得られる結果です。

\[\]

結果によって検定方法を変えると、因果関係が逆転してしまいます。

例えるなら、テストで誤解答した時に、答えに合わせて問題文を変えることと同じです。

答えに合わせて問題を変えては、本末転倒ですよね。

\[\]

まとめ

①第一種の誤りとは、「 本当は帰無仮説\(H_0\) が成り立っているにもかかわらず、これを棄却する誤り 」

②第二種の誤りとは、「 本当は帰無仮説\(H_0\)が成り立っていないにもかかわらず、これを棄却しない誤り 」

③ 「 帰無仮説\(H_0\) を採択し、対立仮説\(H_1\) を棄却した場合 」は「差があるとは言えない」 となる

④ 検出力とは「本当は帰無仮説\(H_0\) が成り立っていないときに、帰無仮説\(H_0\) を棄却する確率」のこと

⑤ P値を求めてから有意水準を決めない！

\[\]

今回は検出力とp値について学びました。

p値については勘違いされることも多いため、気をつけましょう。

\[\]

⇒オススメ書籍はこちら

⇒サイトマップ