信頼性工学 2

公開日2020年10月24日 最終更新日 2021年9月19日
みなさんこんにちは、michiです。
今回は前回の記事で紹介しきれなかった、信頼性工学について勉強していきます。
キーワード:「FMEA」「FTA」
目次
①設計信頼性
設計信頼性とは、設計段階で信頼性を織り込むことです。
主に次の二つの手法があります。
- フェールセーフ
- フールプルーフ
\[\]
フェールセーフ
フェールセーフとは、機械が故障した時に常に安全側に作動する仕組みのことです。
例えば、金属加工装置で異常が発生した場合は、装置そのものが動かなくなる設定などが該当します。
\[\]
フールプルーフ
フールプルーフとは、誤作業を防止する仕組みのことです。
ポカヨケと言われることもあります。
例えば製品の組立ラインで、必要な数量の部品しか供給されないなどの仕組みがあてはまります。
\[\]
フェールセーフとフールプルーフは間違いやすいので注意が必要です。
そもそも間違った作業ができない仕組みがフールプルーフ(ポカヨケ)で、装置や設備が故障しても事故が発生しない仕組みがフェールセーフになります。

\[\]
②FMEA
FMEAとは、Failure Mode Effects Analysis の略称で、故障モード影響解析と呼ばれます。
FMEAは起こりうる可能性のあるトラブルをボトムアップ式で考え評価する方法です。
主に設計FMEAと工程FMEAの2種類があります。
FMEAは下の表をベースに作成します。

ちょっとわかりにくいので、左右に分けて拡大してみます。

「左側」は主に現状の分析が項目として挙げられます。
この表の中で「重要度、発生頻度、検出度」の結果を掛け算し、RPN(リスク)を定量的に評価します。
- 重要度: 数字が大きいほど重大な事故やトラブルになるように設定
- 発生頻度: 数字が大きいほど発生頻度が多くなるように設定
- 検出度:数字が大きいほど発見しづらくなるように設定
いずれも基本的には10段階評価で数値付けをしますが、その点数付けの内容は、作成チーム内で決めていきます。
\[\]
内容を作成チーム内で決める理由は、一般的にはその内容が決まっていないからです。
なぜなら、対象とする設備や工程は様々あり、包括的なルールを一般的に決めるのは難しいからです。
例えば、人の命にかかわるような自動車と、100円均一に売られている便利グッズでは、「重要度、発生頻度、検出度」の基準は同じ内容にはなりません。
\[\]
次にFMEAの「右側」を見てみます。

こちらは、「左側」で分析した定量的なデータや管理方法から、どのように対策していけばよいか、対策の結果はどうなったかをまとめます。
\[\]
それでは実際に、次の例でFMEAを考えてみましょう。

見ての通り、ただのボールペンですが、胸ポケットに引っ掛ける部分についてFMEAを作成してみます。


\[\]
\[\]
さて、よく見ると、対策前の重要度は2で、対策後の重要度も2のままです。
(。´・ω・)?
そうなんです、FMEAでは故障の影響となる「重要度」は対策で変化しないと考えます。
その代わり、発生頻度や検出度を対策で小さくすると考えます。
※今回は検出度は同じという設定です。
\[\]
対策で製品の強度を増やし、故障する頻度を下げることはできました。
しかし、胸ポケットに引っ掛ける部分が壊れた状態は、引っ掛ける部分の強度が増していようがいまいが、壊れてしまったら同じです。
壊れたことによる影響(重要度)は、「失くしやすくなる」は対策では変えられません。
\[\]
FMEAでは、最終的に評価されたRPN(リスク)の数字から、数字の高いものから優先的に改善していくことが多いです。
QC検定では、「FMEAは故障モード毎に、システム全体への影響をボトムアップ式で評価する」と覚えておけば大丈夫です。
詳細はまたの機会に実践編でまとめていこうと思います。
\[\]
③FTA
FTAとは Fault Tree Analysis の略称で、故障の木解析とも呼ばれます。
FTAで使用されるFT図が木の枝だか根に見えることから、故障の木解析と呼ばれます。
FTAは、起こりうる可能性のあるトラブルをトップダウン式で考え評価する方法です。
使用するFT図では、事象と基本事象の間をORゲートやANDゲートでつなげていきます。
FT図のイメージを下に載せます。
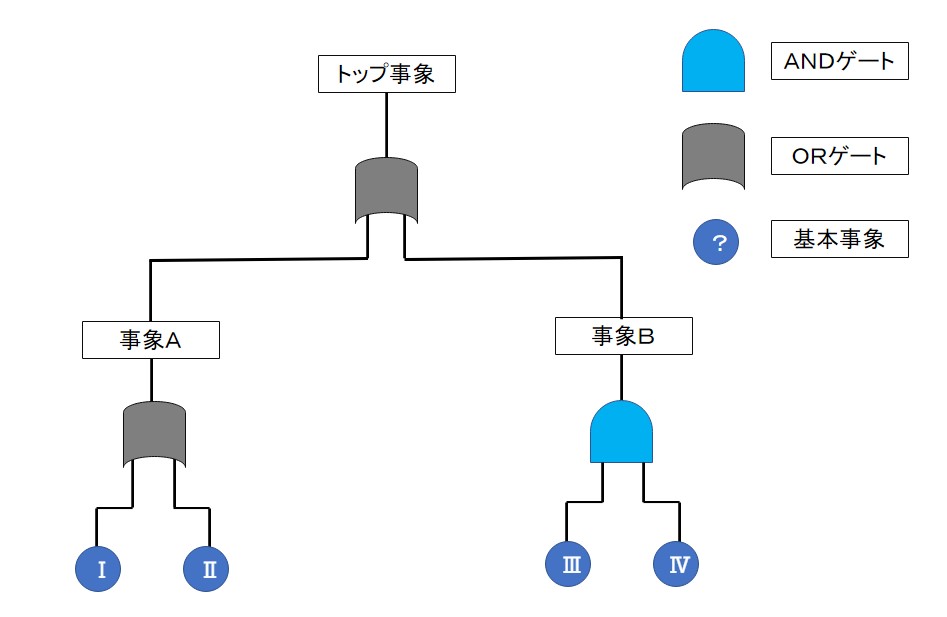
※今回は一段階しか掘り下げていませんが、実際には基本事象がでるまで事象を何度も分解します。
各パーツの意味は次のようになります。
- 事象:基本事象などの組合せで生じた結果
- 基本事象:これ以上細かくできない事象
- ORゲート:入力事象のうち、いずれか一つが存在するときに出力事象が発生
- ANDゲート:入力事象のうち、すべてが存在するときに出力事象が発生
FT図ではトップ事象に対して、各事象の発生確率を計算していきます。
\[\]
ORゲートの場合
ORゲートは、下位の事象のいずれかが発生した場合に上位の事象が発生する状態を表します。
下位の事象が全く発生していない場合は、上位の事象は発生しません。
この時の信頼度は、前回の記事「信頼性工学 1」で学んだ、信頼性ブロック図の直列系を使って計算することができます。
例えば、下図の場合、この系の信頼度は(\(0.98×0.95=0.931\))となります。
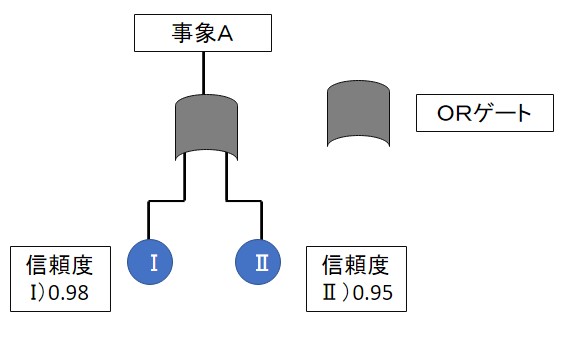
「不信頼度(故障率)=1-信頼度」なので、不信頼度は(\(1-0.931=0.069\))となります。
ORゲートの場合、上位の信頼度が下位の信頼度の積で表される理由は、下位の事象のいずれも発生しない確率が上位の信頼度になるからです。
上の例では事象Ⅰの発生確率は0.98、事象Ⅱの発生確率は0.95ですので、その積である0.931が上位の信頼度になります。
\[\]
ANDゲートの場合
ANDゲートの場合、下位の事象すべてが発生した場合のみ上位の事象が発生する状態を表します。
つまり、いずれかの事象が発生しただけでは上位の事象は発生しません。
この時の信頼度は信頼性ブロック図の並列系で評価することができます。
例えば下図の場合この系の信頼度は(\(1-(1-0.97)×(1-0.93)=0.9979\))となります。
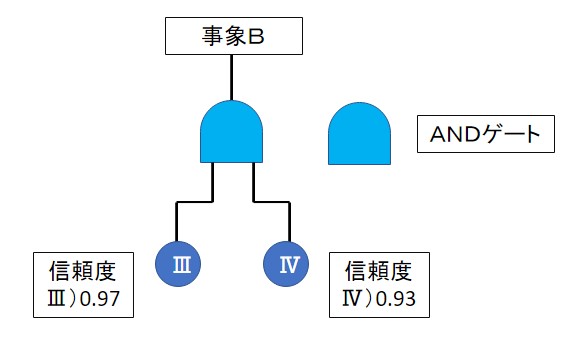
「不信頼度=1-信頼度」なので、不信頼度は(\(1-0.9979=0.0021\))となります。
ANDゲートの場合、上位の不信頼度(故障率)が下位の不信頼度(故障率)の積で表される理由は、下位の事象のどちらも発生する確率が上位の不信頼度(故障率)になるからです。
上の例では事象Ⅲの故障確率は\((1-0.97=0.03)\)、事象Ⅱの故障確率は\((1-0.93=0.07)\)ですので、その積である0.0021が上位の不信頼度(故障率)になります。
\[\]
以上を踏まえ、例で挙げたFT図をもう一度見てみましょう。
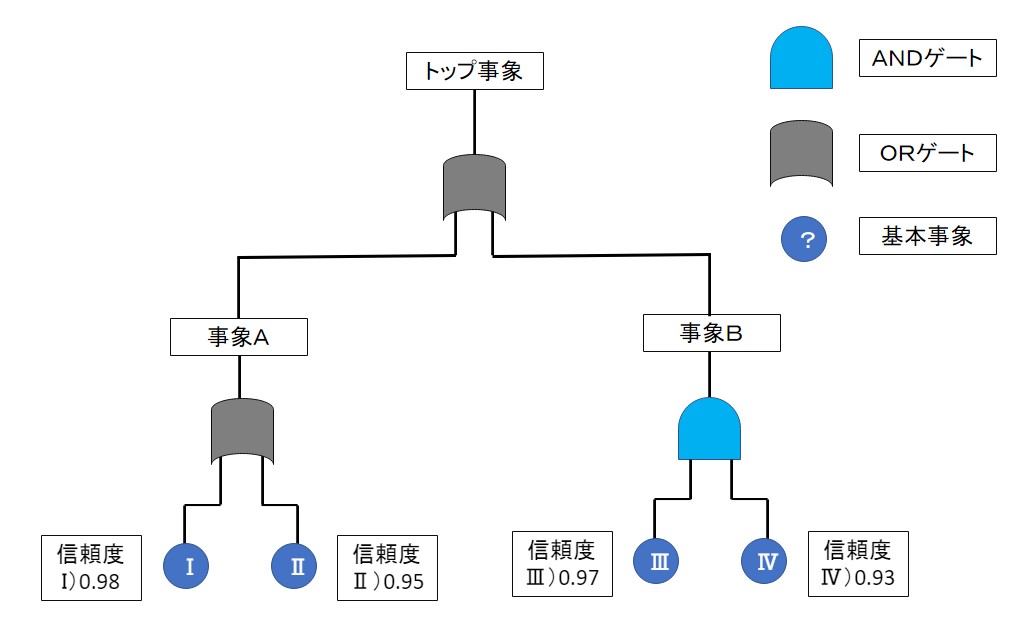
\[\]
FTAは事象をORゲートとANDゲートでそれ以上分解できない基本事象まで分解します。
最終的にどの基本事象が、トップ事象を引き起こした可能性が高いかを定量的に評価します。
トップ事象はORゲートで繋がっていることから、事象Aまたは事象Bによっ引き起こされています。
事象Aと事象Bの信頼度を比較すると、事象Aの方が信頼度が低い(故障率が高い)ことが分かります。
トップ事象の発生を抑えるには、事象Aの対策を優先すべきと判断できます。
\[\]
④FMEAとFTAのポイント
FMEAとFTAの違いは、ボトムアップ式で考えるか、トップダウン式で考えるかの違いです。
本質的には同じで、要因と現象を定量的に評価しようとする試みです。
ポイントは、KKD(経験、勘、度胸)ではなく客観的な事実から分析することです。
そのため、FMEAとFTAでは「人のせいにしない」ことが重要になります。
\[\]
具体例を考えてみます。
例えば、製品Aの組み立て作業で不具合が発生したとします。
この時、要因分析の結果「組立作業者Bさんのミス」で結論づけてはいけません。
この場合は「組立作業者Bさんのミス」をさらに分解し、真の基本事象にまで分解する必要があります。
その結果、例えばマニュアルの不備が発見され、本質的な解決策である「マニュアルの見直し・整備」が実施されます。
確かに不具合の原因は「組立作業者Bさんのミス」であっても、さらにそれを誘発させた原因まで突き詰めて考えることが重要になります。
\[\]
不具合の原因を人のせいにしている状態は、品質が個人の技量に頼ってしまっている状態です。
個人の技量に頼った状態では、客観的な分析や本質的な解決は難しいままです。
FMEA,FTAに限らず、分析は客観的な事実に基づく分析を心掛けましょう。

\[\]
⑤なぜなぜ分析
なぜなぜ分析はみなさん一度は聞いたことがあると思います。
これはトヨタ社で提唱され、広まった考え方です。
\[\]
なぜなぜ分析はFTAと同様にトップダウンで事象の発生要因を考える手法です。
なぜなぜ分析は最低限5回は「なぜ」を繰り返して分析することが推奨されています。
「なぜ(Why)」を5回繰り返せば、本質的な原因にたどり着けるという考えです。
FTAのように定量的な数値の評価はしませんが、最終的に「なぜ」を繰り返して得られた分析結果を評価します。
\[\]
なぜなぜ分析はQC検定にこそほとんど出題されませんが、実際の業務では使われているところも多いのではないでしょうか。
さらに業務上のトラブルだけではなく、日常の生活でも活かせる手法だと私は考えます。
例えば、子供の落ち着きがない⇒なぜ?⇒なぜ?・・・⇒!!Σd(・∀・)ナルホド!!
最近体重が増えてきた⇒なぜ?⇒なぜ?・・・⇒!!Σd(・∀・)ナルホド!!
といった感じです。

\[\]
まとめ
①設計信頼性には、フェールセーフとフールプルーフの考え方がある
②FMEAは故障モードの影響をボトムアップ式で考える
③FTAは故障の原因をトップダウン式で考える
④FMEAとFTAのポイントは、「人のせいにしない!」
⑤なぜなぜ分析は、日常生活でも使える手法!
\[\]
今回は信頼性工学2 ということで、前回の記事「信頼性工学 1」で紹介しきれなかった内容を学びました。
次回はQC7つ道具について勉強していきましょう!
\[\]














[…] また、前回の記事「信頼性工学 2」で紹介したなぜなぜ分析を思い出してみても良いです。 […]