公開日2020年5月8日 最終更新日 2021年9月20日
みなさんこんにちは、michiです。
前回はF検定について学びました。そこで以下の式変形をしましたね。
\[棄却限界値 F(Φ_2,Φ_1:0.975)=\frac{1}{棄却限界値 F(Φ_1,Φ_2:0.025)}\]
もう少し一般的な形にすると
\[棄却限界値 F(Φ_2,Φ_1:1-α)=\frac{1}{棄却限界値 F(Φ_1,Φ_2:α)}\]
今回は、F検定の棄却域を求めるときに、上記の式変形が成り立つ理由を勉強します。
キーワード:「逆数」「1-\(α\)」「統計量\(F\)」
\[\]
目次
①下側の棄却域は\(1-α\)%
前回の両側検定を思い出してみます。
この時は第一種の誤り\(α\)を5% として、上側の棄却域の面積が2.5%になるように設定しました。
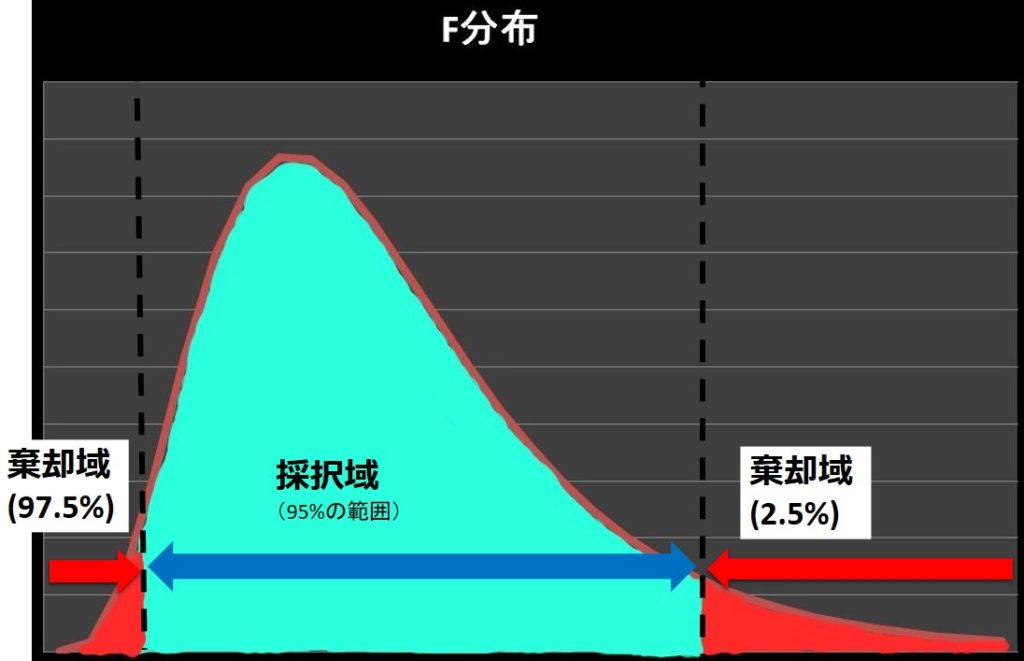
上の図を簡単に説明すると、右側からグラフの面積を足していき、面積が全体の2.5%になったときの横軸の値が、右側の棄却限界値となります。
※棄却限界値より右側の累積した面積が確率になります。
次に、右側の棄却域の面積 = 2.5% = 左側の棄却域の面積となるように、下側の棄却域を求めます。
(。´・ω・)? どうすれば?
\[\]
グラフの面積は右側から足していくので、グラフの面積が全体の 97.5% となるときの横軸の値を求めます。
この時、以下の特徴を考えると、下のグラフのようになります。
- グラフの全面積の合計は 1 (=100%)
- 左右の棄却域の面積(確率)は同じ
- グラフの面積は右側から足していく

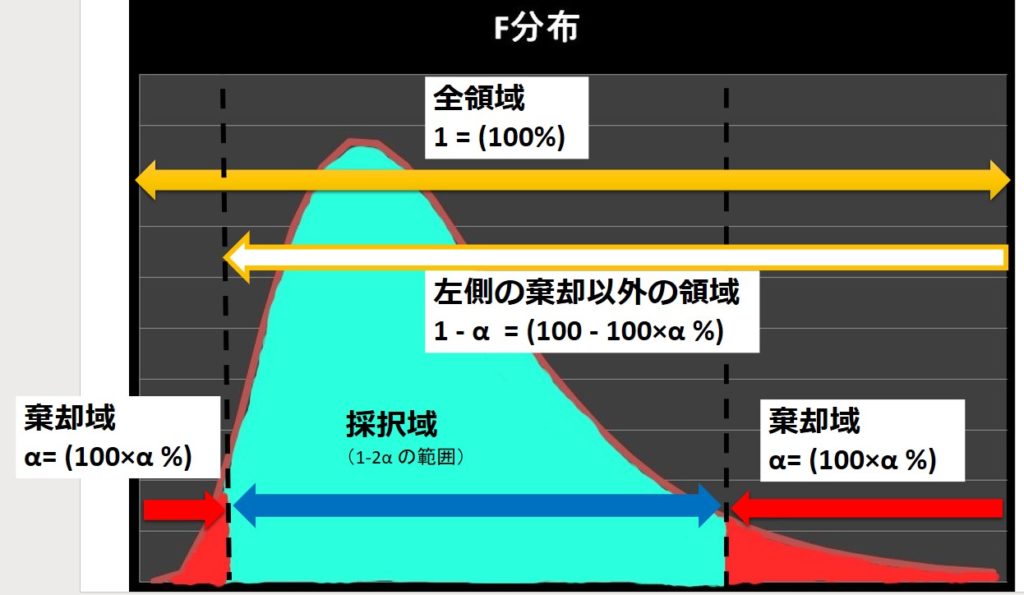
上の図のように、右からの面積を足していき、面積が全体の97.5%となるときの横軸の値が左側の棄却限界値となります。
\[\]
もう少し一般的な形にするために、右側の棄却限界値を求めるときの確率を\(α\)とします。
すると、左側の棄却限界値を求めるときの確率は\(1-α\) になります。
\[\]
②統計量\(F\)は比率のこと
統計量\(F\)は、二つの集団の不偏分散を\(F\)>1になるように割り算し、二つの集団のばらつきを評価する統計量でした。
\[F\qquad =\frac{V_B}{V_A} \qquad >1\]
分かりやすくするために、具体的な数値を入れます。
\(V_B\)の自由度が 8 、\(V_A\)の自由度が 9 で、両側検定を実施。第一種の誤りを 5%とします。
この時の棄却限界値は、確率P= 0.025 の\(F\)表より、\(F(8,9:0.025)\)=4.10 となります。
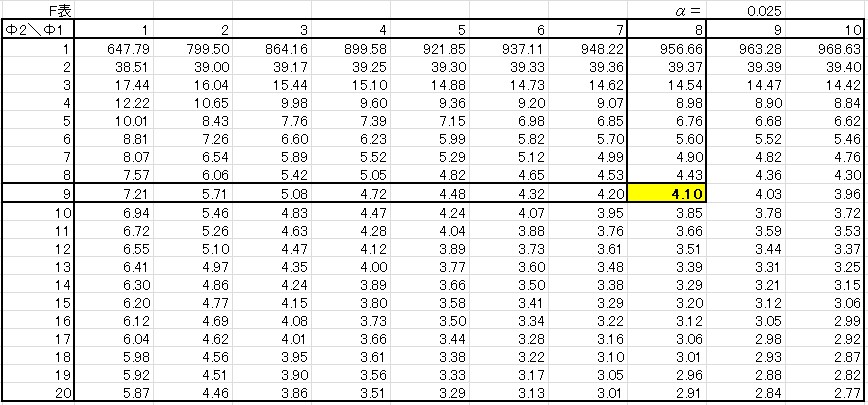
よって、
\[F(8,9:0.025)\qquad =\frac{V_B}{V_A}\qquad=4.10\]
ですが、以下のように考えてみましょう。
\[\frac{V_B}{V_A}\qquad=4.10 \qquad =\frac{4.10}{1}\]
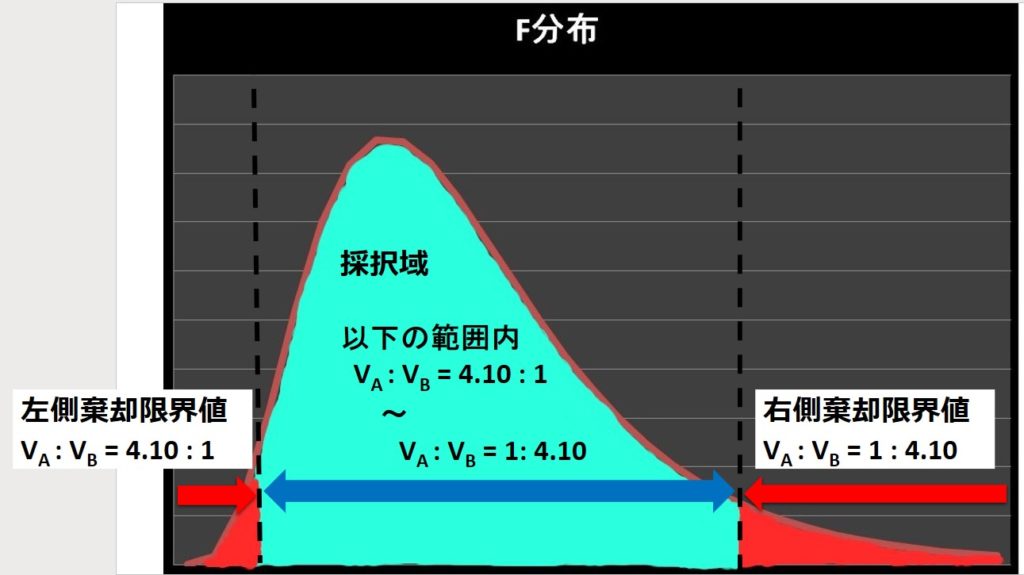
\[V_A:V_B=1:4.10\]
統計量\(F\)>1 というのは、 \(V_A:V_B=1:4.10\) より、分子の\(V_B\)の不偏分散が分母の\(V_A\)の不偏分散よりも 4.10 倍以上大きくなる条件と言い換えられます。
\[\]
ここで、統計量\(F\)は棄却限界値をあらわしているので、もう少し一般的に言い換えれば
「自由度8の集団Bと自由度9の集団Aの不偏分散を比べた時に、4.10倍以上差がつくと、二つの集団のばらつきは同じといえない」 となります。
先ほどは、「\(V_B\)の不偏分散が\(V_A\)の不偏分散よりも 4.10 倍以上大きくなる」ときを考えましたが、その逆も成り立ちます。
\[\]
左側の棄却限界値の条件 「\(V_A\)の不偏分散が\(V_B\)の不偏分散よりも 4.10 倍以上大きくなる」 を数式で表すと、
\[V_A:V_B=4.10:1\]
\[\frac{V_B}{V_A}\qquad= \frac{1}{4.10}\]
この時の統計量を\(F’\)とすると、
\[F’\qquad=\frac{V_B}{V_A}\qquad=\frac{1}{4.10}\]
\[\]
え・・・検定統計量\(F\)>1 なんじゃ・・・
(。´・ω・)?
\[\]
はいそうです。
ただしそれは「右側(上側)の棄却限界値を求める条件」です。
左側(下側)の棄却限界値を求めるには、検定統計量\(F’\)<1 が条件になります。
以上より、
\[左側(下側)の棄却限界値 \qquad = \qquad \frac{1}{右側(上側)の棄却限界値}\]
となります。
\[\]
③自由度が逆になる理由
もう一度冒頭の式をみてみると、
\[棄却限界値 F(Φ_2,Φ_1:1-α)=\frac{1}{棄却限界値 F(Φ_1,Φ_2:α)}\]
以下の内容について確認しました。
- 右側の棄却域\(α\)に対し、左側の棄却域が\(1-α\)になる理由
- 右側の棄却限界値の逆数が左側の棄却限界値になる理由
最後に自由度\(Φ_1\)と自由度\(Φ_2\)が入れ替わる理由を考えます。
\[\]
\(F=\frac{V_B}{V_A}\) と書けるときの棄却限界値は、
棄却限界値\(F\)(自由度\(Φ_1\),自由度\(Φ_2\):第一種の誤り\(α\))でした。
この時の自由度\(Φ_1\)は、分子(\(V_B\))の不偏分散の自由度でした。
左側(下側)の棄却限界値は、
\[F’ \qquad = \frac{V_A}{V_B}\]
なので、棄却限界値\(F’\)の最初にくる自由度(横軸の自由度)は、分子の不偏分散\(V_A\)の自由度になります。
左側の棄却限界値は右側の棄却限界値の逆数になるため、分母と分子が入れ替わり、最初の自由度(横軸の自由度)も入れ替わります。
\[\]
よって、
\[棄却限界値 F(Φ_2,Φ_1:1-α)=\frac{1}{棄却限界値 F(Φ_1,Φ_2:α)}\]
\[\]
まとめ
①左側の棄却限界値は右側から面積を求めるため、\(1-α\)%で考える
②左側の棄却限界値は右側の棄却限界値の逆数になる
③左側の棄却限界値は右側の棄却限界値の逆数なので、自由度も逆になる。
\[\]
次回は平均に関する推定について勉強していきましょう!
















[…] 次回はなぜこの式(F分布の下側棄却域)が成立するのかと、その意味を勉強しましょう。 […]