定量的なサンプリング とは

公開日2021年8月31日 最終更新日 2021年9月26日
みなさんこんにちは、michiです。
前回は超幾何分布について勉強しました。
今回はその応用として、有限母集団からのサンプリングについて学んでいきます。
サンプリングの種類については、記事「サンプリングの種類」にまとめていますが、そこで学んだ知識を具体的に数値で考えていきます。
ただし、系統サンプリングと有意サンプリングは今回の対象ではありません。
キーワード:「有限修正」「ばらつきは加算」
目次
①ランダムサンプリング
ランダムサンプリングとは、「母集団からランダムにサンプリングすること」になります。
母平均が \(μ\) 、母分散が \(σ^2\) の大きさ \(N\) の有限母集団から、ランダムに \(n\) 個抜き取った場合の、平均値 \(\bar{x}\) の期待値 (\(E(\bar{x})\))と分散 (\(V(\bar{x})\))は次のようになります。
\[E(\bar{x})=μ\]
\[V(\bar{x})=\frac{N-n}{N-1}・\frac{σ^2}{n}\]
- \(N\):有言母集団の大きさ
- \(n\):抽出したサンプルの大きさ
- \(σ^2\):母の分散
\[\]
母平均が \(μ\) の母集団からランダムにサンプリングするので、サンプルの平均値の期待値(\(E(\bar{x})\))が、母平均 \(μ\) と同じになることは想像できます。
注目すべきは分散です。
分散には有限修正 \(\frac{N-n}{N-1}\) があります。
有限修正があるということが、無限母集団の分散 \(V(\bar{x})=\frac{σ^2}{n}\) と異なる点です。
\[\]
また、平均値 \(\bar{x}\)の分散 (\(V(\bar{x})\))とは、サンプリングしたデータの平均値のばらつきを表します。
紛らわしいですが、間違えないようにしましょう。
\[\]
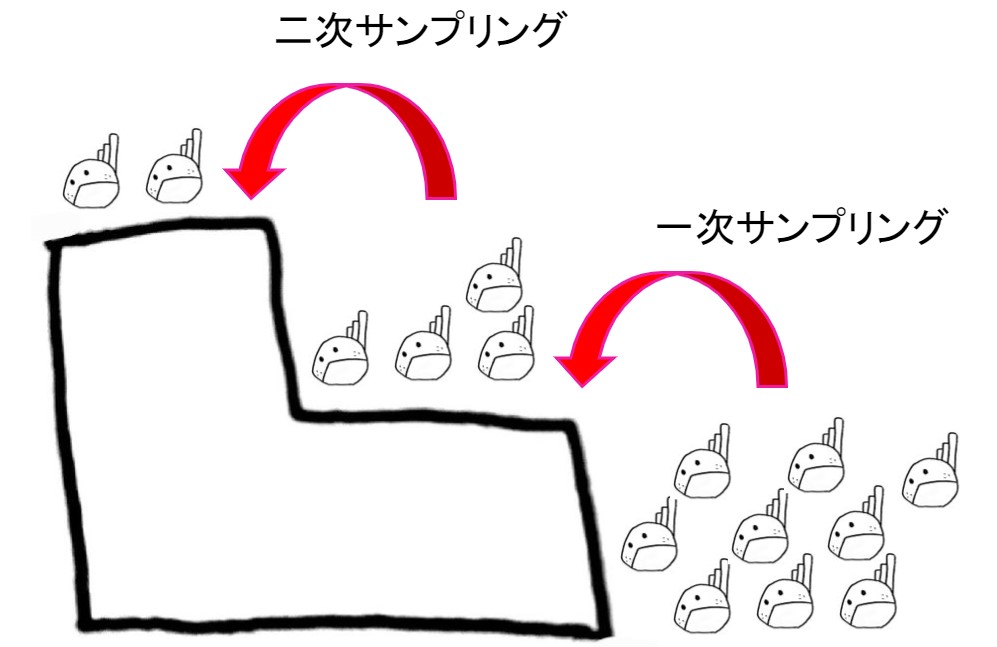
②二段サンプリング
2段サンプリングとは、「母集団からいくつかのサンプルを採り、さらに各サンプル内でいくつかのサンプルを採ること」です。
ランダムサンプリングと同様に考えていきます。
母平均が \(μ\) の有限母集団の二段サンプリングの平均値 \(\bar{x}\)の期待値(\(E(\bar{x}\))) と分散(\(V(\bar{x}\)))は次のようになります。
\[\]
\[E(\bar{x})=μ\]
\[V(\bar{x})=\frac{M-m}{M-1}・\frac{σ_b^2}{m}+\frac{N-n}{N-1}・\frac{σ_ω^2}{mn}\]
- \(M\):一次単位の総数
- \(N\):一次単位の大きさ
- \(m\):一次サンプルの大きさ
- \(n\):二次サンプルの大きさ
- \(σ_b^2\):一次単位間の特性 \(x\) の分散
- \(σ_ω^2\):一次単位内の特性 \(x\) の分散
\[\]
_(:3 」∠ )_
かなり複雑ですね。
しかし、二次サンプリングをしっかり理解することで、層別サンプリングと集落サンプリングが分かるようになります。
頑張りましょう!
╭( ・ㅂ・)و̑ グッ
\[\]
さて、比較のために無限母集団の場合の平均値 \(\bar{x}\)の期待値(\(E(\bar{x}\))) と分散(\(V(\bar{x}\)))を見てみましょう。
\[E(\bar{x})=μ\]
\[V(\bar{x})=\frac{σ_b^2}{m}+\frac{σ_ω^2}{mn}\]
- \(M\):一次単位の総数
- \(N\):一次単位の大きさ
- \(m\):一次サンプルの大きさ
- \(n\):二次サンプルの大きさ
- \(σ_b^2\):一次単位間の特性 \(x\) の分散
- \(σ_ω^2\):一次単位内の特性 \(x\) の分散
\[\]
有限母集団の場合と比べると、少しだけ簡単になっていますね。
具体的には、「\(\frac{M-m}{M-1}\)」と「\(\frac{N-n}{N-1}\)」がありません。
①ランダムサンプリングと同様に、有限母集団の2段サンプリングもまた、無限母集団の2段サンプリングに係数「\(\frac{M-m}{M-1}\)」と「\(\frac{N-n}{N-1}\)」がかけられているだけです。
「\(\frac{M-m}{M-1}\)」と「\(\frac{N-n}{N-1}\)」は、どちらも有限修正です。
\[\]
さて、有限修正がかけられていることはわかったので、「+」の前の項「\(\frac{M-m}{M-1}・\frac{σ_b^2}{m}\)」にまずは着目します。
説明を見ると、 \(σ_b^2\) は「一次単位間の特性 \(x\) の分散」と書かれています。
2段サンプリングは、ランダムサンプリングを2回繰り返すイメージでした。
その1回目にあたるのが、「\(\frac{M-m}{M-1}・\frac{σ_b^2}{m}\)」 になります。
(。 ・ω・))フムフム
\[\]
\(M → N\) 、 \(m → n\) としてみましょう。
\(\frac{M-m}{M-1}・\frac{σ_b^2}{m}\) ⇒ \(\frac{N-n}{N-1}・\frac{σ_b^2}{n}\)
①ランダムサンプリングで学んだ式と同じになりましたね。
1回目の抽出するいくつかのグループ間に対してそのばらつきを見ているので、「一次単位間の特性 \(x\) の分散」となるわけです。
\[\]
次に「+」の後ろの項「\(\frac{σ_ω^2}{mn}\)」について考えます。
説明を見ると、 \(σ_ω^2\) は「一次単位内の特性 \(x\) の分散」と書かれています。
1次サンプリングで総数 \(M\) 個の中から \(m\) 個サンプリングしました。
\(m\) 個の中には、それぞれ \(N\) 個のサンプルが入っています。
2次サンプリングでは、その \(N\) 個の中から \(n\)個サンプリングします。
\[\]
2次サンプリングだけを考えると、有限修正「\(\frac{N-n}{N-1}\)」がかけられていることも納得できます。
ただし、\(σ_ω^2\) を考える時に気をつけることがあります。
それは、「\(\frac{σ_ω^2}{mn}\)」 と分母が \(mn\) となっていることです。
この理由は単純で、\(N\) 個の中から\(n\) 個をサンプリングしましたが、そもそも \(N\) 個は \(m\) 個あるため、掛け算をしているわけです。
\[\]
したがって、「\(\frac{N-n}{N-1}・\frac{σ_ω^2}{mn}\)」は、一次サンプリングで得たサンプル内のばらつきを表すことになります。
ややこしいですが、しっかり理解しましょう!
\[\]
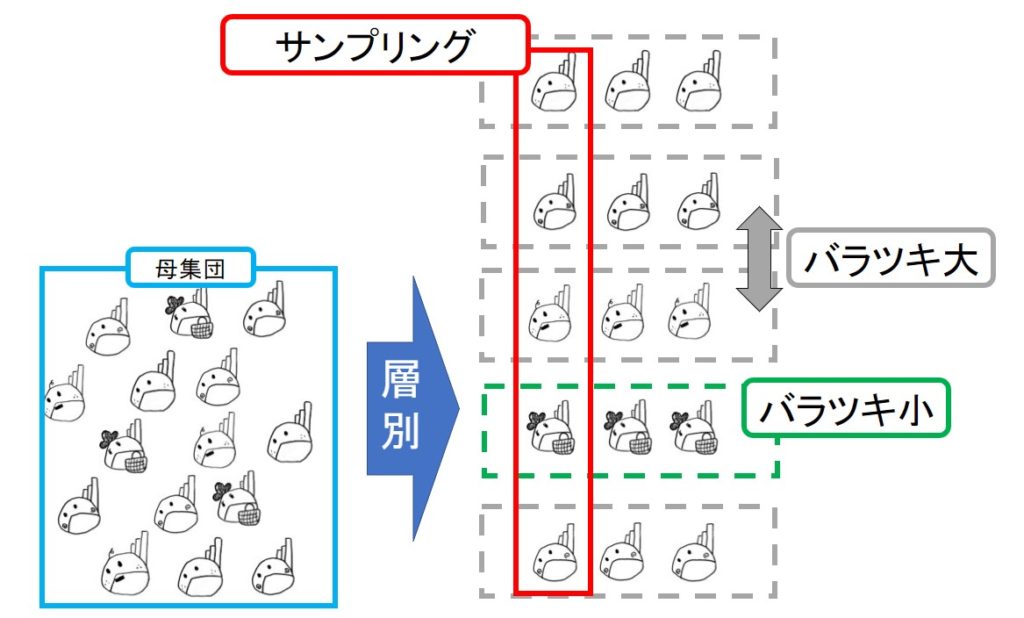
③層別サンプリング
層別サンプリングとは、「いくつかの層に分け、その分けた層からサンプリングすること」です。
母平均が \(μ\)の有言母集団における層別サンプリングの期待値と分散は次のようになります。
\[E(\bar{x})=μ\]
\[V(\bar{x})=\frac{N-n}{N-1}・\frac{σ_ω^2}{Mn}\]
- \(M\):一次単位の総数
- \(N\):一次単位の大きさ
- \(n\):二次サンプルの大きさ
- \(σ_ω^2\):一次単位内の特性 \(x\) の分散
\[\]
\(σ_ω^2\) は一次単位内の特性 \(x\) の分散です、
2段サンプリングと比較すると、\(σ_b^2\):一次単位間の特性 \(x\) の分散 がありません。
一次単位間の分散がない理由は、層別サンプリングにおいては一次単位間で同じような性質のデータを抽出するためです。
一次単位間で同じようなデータを抽出するため、一次単位間のばらつき \(σ_b^2\) はゼロと考えるわけです。
考えるべきは一次単位内の分散のみで、\(M=m\) となります。
\[\]
④集落サンプリング
集落サンプリングとは、「母集団をいくつかの集落(クラスター)に分けてサンプリングし、その集落の全数をサンプリングすること」となります。
母平均が \(μ\)の有言母集団における集落サンプリングの期待値と分散は次のようになります。
\[E(\bar{x})=μ\]
\[V(\bar{x})=\frac{M-m}{M-1}・\frac{σ_b^2}{m}\]
- \(M\):一次単位の総数
- \(m\):一次サンプルの大きさ
- \(σ_b^2\):一次単位間の特性 \(x\) の分散
\[\]
\(σ_b^2\)は、一次単位間の特性 \(x\) の分散です。
二段サンプリングと比較すると、\(σ_ω^2\) 一次単位内の特性 \(x\) の分散 がありません。
これは集落サンプリングにおいては、一次単位内のデータすべてを抽出するためです。
一次単位内のすべてのデータを抽出するため、一次単位内のばらつき \(σ_ω^2\) はゼロと考えるわけです。
考えるべきは、一次単位間の分散 \(σ_b^2\)のみ になります。
\[\]
⑤2段サンプリングから考える
さて、これまでを4つのサンプリング方法を解説してきました。
- ①ランダムサンプリング
- ②2段サンプリング
- ③層別サンプリング
- ④集落サンプリング
\[\]
ポイントは2段サンプリングから考えることです。
なぜなら、2段サンプリングでは一次単位間の分散 \(σ_b^2\) と、一次単位内の分散 \(σ_ω^2\) の両方を考えているためです。
層別サンプリングであれば、一次単位間の分散 \(σ_b^2\) はゼロとなり、集落サンプリングであれば、一次単位内の分散 \(σ_ω^2\) はゼロと考えます。
\[\]
単純ランダムサンプリングを考える場合は、集落サンプリングにおいて \(M⇒N\)、 \(m⇒n\) とすれば求められます。
\[\]
このように考えると、2段サンプリングの公式さえ覚えてしまえば、単純ランダムサンプリング、層別サンプリング、集落サンプリングを網羅できることが分かります。
日科技連のテキストにはわかりやすい例題があるので、ぜひ読んでみてください。
\[\]
⑥分散(ばらつき)は加算される
最後に考え方を少し拡張させて、ばらつきが加算されることについて考えます。
「ばらつきは加算される」そんなことは知っているという人も多いでしょう。
実際QC検定2級レベルの受験者であっても、この言葉は知っておくべきです。
\[\]
さて、今回は様々なサンプリングを考えましたが、2段サンプリングを基本に考えると理解しやすい内容でしあた。
復習ですが、母平均が \(μ\) の有限母集団の二段サンプリングの期待値と分散は次のようになります。
\[\]
\[E(\bar{x})=μ\]
\[V(\bar{x})=\frac{M-m}{M-1}・\frac{σ_b^2}{m}+\frac{N-n}{N-1}・\frac{σ_ω^2}{mn}\]
- \(M\):一次単位の総数
- \(N\):一次単位の大きさ
- \(m\):一次サンプルの大きさ
- \(n\):二次サンプルの大きさ
- \(σ_b^2\):一次単位間の特性 \(x\) の分散
- \(σ_ω^2\):一次単位内の特性 \(x\) の分散
\[\]
有限修正を無視して、無限母集団として考えると、2段サンプリングの分散は次のようになります。
\[V(\bar{x})=\frac{σ_b^2}{m}+\frac{σ_ω^2}{mn}\]
分母の 「\(m\)」「\(mn\)」は、抽出したサンプル数になります。
無限母集団における分散「\(\frac{σ_b^2}{m}+\frac{σ_ω^2}{mn}\)」は、
1サンプルあたりの「一次単位間サンプルのばらつき + 一時単位内サンプルのばらつき」を表します。
\[\]
たしかに、一次単位間のばらつき \(σ_b^2\) と、一次単位内のばらつき \(σ_ω^2\) が加算されています。
今回はサンプリングを例として考えたため、分母に \(m\) や \(mn\) といった数値があります。
これらを一般化すると、ばらつきは次のようになります。
\[σ_全^2=σ_A^2+σ_B^2+σ_C^2+・・・\]
- \(σ_全^2\):全体に分散
- \(σ_A^2\):要因Aによる分散
- \(σ_B^2\):要因Bによる分散
- \(σ_C^2\):要因Cによる分散
\[\]
このように全体の分散 \(σ_全^2\) は、各要因の分散の和で表されます。
ポイントは、「加算されるのは分散であって、標準偏差ではない」ということです。
\[\]
例えば、ばらつきの要因として、装置間のばらつき、日間のばらつき、サンプル間のばらつきがあるとします。
この場合、全体のばらつきは全体の分散として表すことができ、その全体の分散は「装置間の分散」「日間の分散」「サンプル間の分散」の和で表されます。
\[\]
まとめ
①ランダムサンプリングの期待値と分散
\[E(\bar{x})=μ\]
\[V(\bar{x})=\frac{N-n}{N-1}・\frac{σ^2}{n}\]
- \(N\):有言母集団の大きさ
- \(n\):抽出したサンプルの大きさ
- \(σ^2\):母の分散
②2段サンプリングの期待値と分散
\[E(\bar{x})=μ\]
\[V(\bar{x})=\frac{M-m}{M-1}・\frac{σ_b^2}{m}+\frac{N-n}{N-1}・\frac{σ_ω^2}{mn}\]
- \(M\):一次単位の総数
- \(N\):一次単位の大きさ
- \(m\):一次サンプルの大きさ
- \(n\):二次サンプルの大きさ
- \(σ_b^2\):一次単位間の特性 \(x\) の分散
- \(σ_ω^2\):一次単位内の特性 \(x\) の分散
③層別サンプリングの期待値と分散
\[E(\bar{x})=μ\]
\[V(\bar{x})=\frac{N-n}{N-1}・\frac{σ_ω^2}{Mn}\]
- \(M\):一次単位の総数
- \(N\):一次単位の大きさ
- \(n\):二次サンプルの大きさ
- \(σ_ω^2\):一次単位内の特性 \(x\) の分散
④集落サンプリングの期待値と分散
\[E(\bar{x})=μ\]
\[V(\bar{x})=\frac{M-m}{M-1}・\frac{σ_b^2}{m}\]
- \(M\):一次単位の総数
- \(m\):一次サンプルの大きさ
- \(σ_b^2\):一次単位間の特性 \(x\) の分散
⑤2段サンプリングからランダムサンプリング、層別サンプリング、集落サンプリングを考える
⑥ばらつきは加算される
\[\]