直交配列実験とは 3 3水準
公開日2022年3月5日 最終更新日 2022年4月24日
みなさんこんにちは、michiです。
前回までは基本となる直交配列表を使った2水準系実験を学びました。
今回は3水準の直交配列実験について学んでいきます。
キーワード:「直交配列表」

目次
実施手順
3水準の直交配列実験は、2水準の直交配列実験と同じ手順で行います。
- ①取り上げる交互作用の決定
- ②割り付け
- ③実験の実施
- ④計算補助表の作成
- ⑤列平方和の計算
- ⑥分散分析の実施
- ⑦データの構造式の確認
- ⑧最適条件における母平均の推定
- ⑨母平均の差の推定
- ⑩最適水準におけるデータの予測
\[\]
相変わらずやることが多いです。
(´・ω・`;)
前回と同様に、①~⑧までは理解しておきましょう。
それでは、ひとつずつ解説していきます。
\[\]
①取り上げる交互作用の決定
取り上げる交互作用を決めます。
ただし、3水準系の直行配列表は一番実験回数の少ないもので \(L_9(3^4)\) となります。
\(L_9(3^4)\) 直交配列表では、4つの因子まで取り上げることができます。
実験回数は9回です。
(´・∀・`)ヘー
\[\]
しかし、交互作用を考えるのであれば、 \(L_{27}(3^{13})\) 直交配列表を使う必要があります。
\(L_{27}(3^{13})\) 直交配列表では、13個の因子まで取り上げることができます。
実験回数は27回です。
( ¯•ω•¯ )メンドー
\[\]
\(L_{27}(3^{13})\) 直交配列表 は次の通りです。
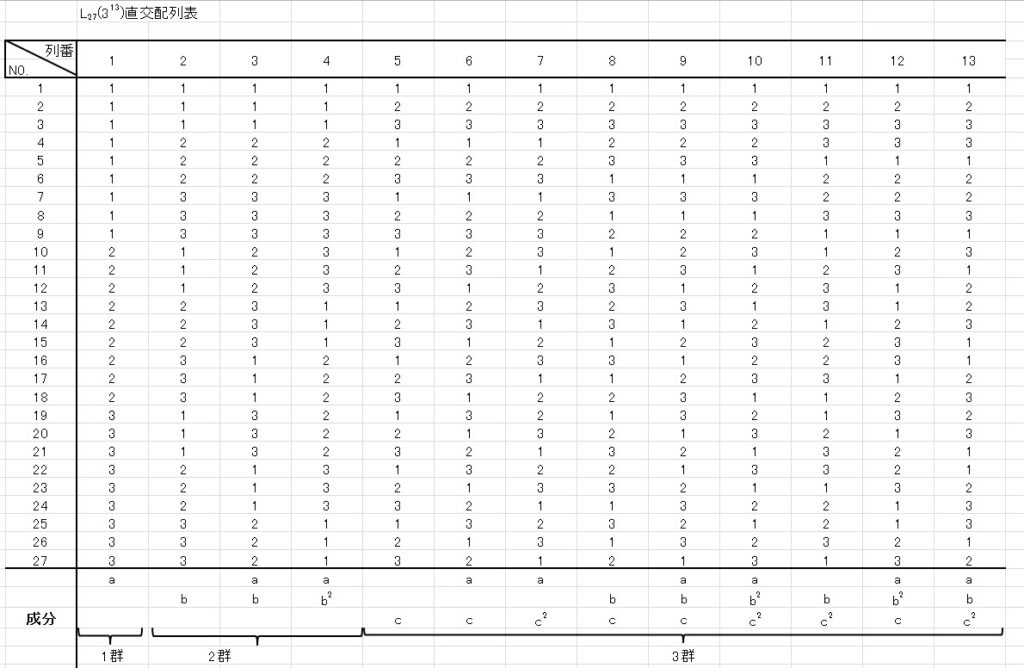
( ºωº )
2水準とは比べ物にならないほど複雑ですね。
\[\]
②割り付け
割り付けも2水準の直交配列実験と同じように行います。
2水準では主効果の自由度は「1」なので、交互作用の自由度は「1×1=1」でした。
しかし、3水準では主効果の自由度は「2」なので、交互作用の自由度は 「2×2=4」 となります。
\[\]
2水準の直交配列表では各列の自由度が 1 でした。
3水準の直交配列表では各列の自由度は 2 になります。
つまり、一つの主効果に対しては一つの列を割り付けることができますが、交互作用は自由度が 4 なので二つの列に表れることになります。
\[\]
①成分による割り付け
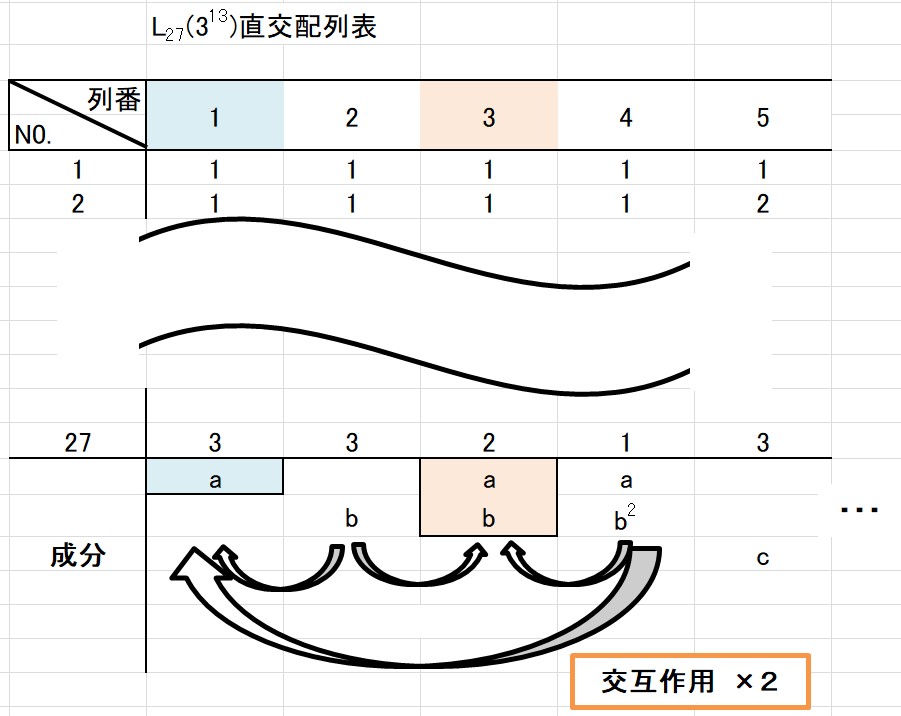
\(L_{27}(3^{13})\) 直交配列表の成分を見てください。
第3列に \(ab\) 、第4列に \(ab^2\) と書かれています。
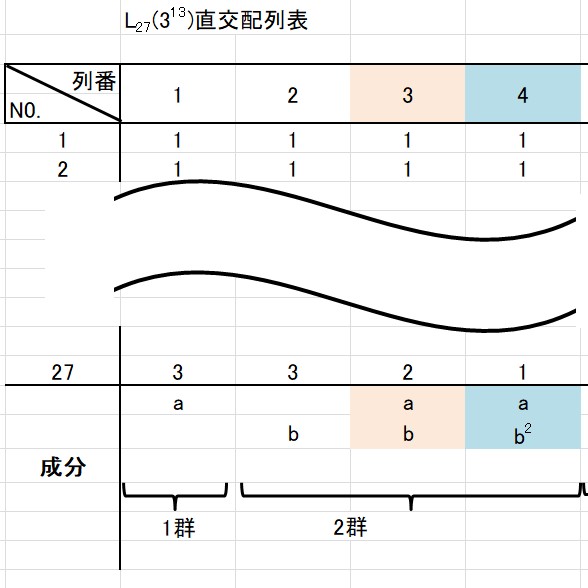
\[\]
第1列の成分が \(a\) で、第2列の成分が \(b\) なので、その成分同士をかけた結果が \(ab\) というのは、2水準の直交配列実験と同じです。
(。 ・ω・))フムフム
実は、第4列の成分 \(ab^2\) もまた第1列と第2列の交互作用を表す列となります。
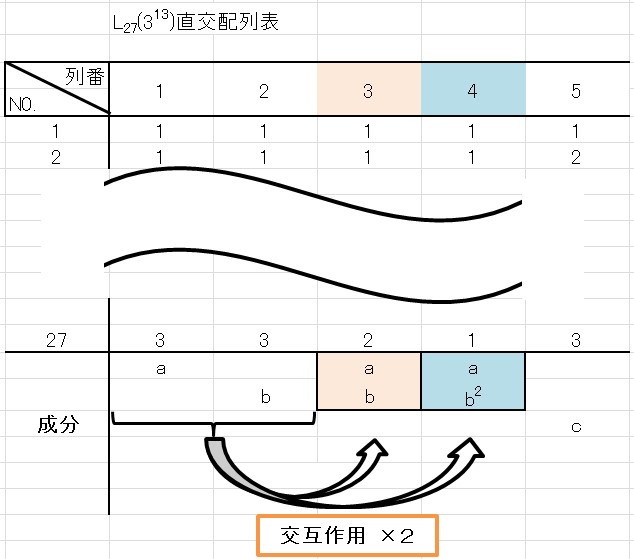
\[\]
成分の考え方で、2水準の直交配列実験では、「二乗すると1」になりました。
3水準の直交配列実験では、「三乗すると1」になります。
\[\]
例えば第2列の成分\(b\) と第4列の成分\(ab^2\) に主効果を割り付けたとします。
この時の交互作用がどの列に表れるかというと…
\[b \times ab^2 = ab^3 =a \times 1 = a \]
成分\(a\) の第1列に表れます。
\[\]
(。´・ω・)ん?
3水準の直交配列実験では、交互作用が2列に表れると説明しました。
しかし、今のところ1列しか見つけられていません。
交互作用が表れるもう1列は、どうやって見つければよいのでしょうか?
\[\]
?(・ω・*≡*・ω・)?
答えは「どちらかの成分を二乗」します。
先ほどの例で考えてみましょう。
第4列の成分\(ab^2\) を二乗してみます。
\[b \times (ab^2)^2 = a^2b^4 =a^2b \]
\[\]

( ゚д゚) ・・・
(つд⊂)ゴシゴシ
直交配列表の成分を見ると、「\(a^2b\)」の成分はどこにもありません!
二乗する成分を間違えたようです。
そこで、 第2列の成分\(b\) を二乗して計算してみます。
\[b^2 \times ab^2 = ab^4 =ab \]
\[\]
成分「\(ab\)」であれば、第3列にあります。
以上のことから、第2列と第4列に主効果を割り付けた場合、その交互作用は第1列と第3列に表れます。
※第1列と第2列に主効果を割り付けた場合の、交互作用が表れる列も考えてみましょう。
答えは、ここまでの記事を読み返すとわかります!
\[\]
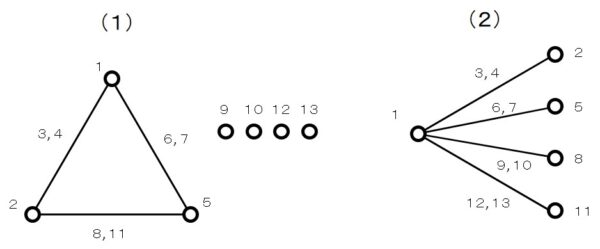
②線点図を使った割り付け
線点図を使った割り付けも、考え方は2水準と同じになります。
\(L_9(3^4)\) 直交配列表の線点図は次のとおりです。
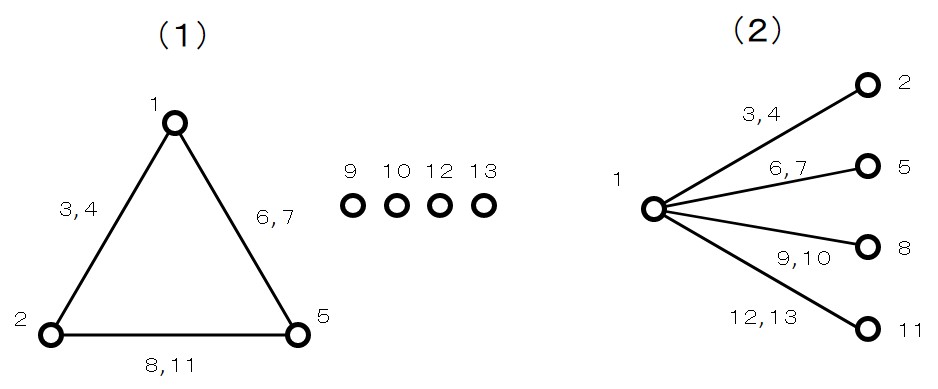
\[\]
なんだか、2水準の線点図 \(L_8(2^7)\) に似ていますよね。
(´-ω-)ウム

\[\]
しかし、よく見ると \(L_9(3^4)\) 直交配列表の線点図では、線に二つの数字が割り当てられています。
これは、二つの点(主効果)の間に二つの線(交互作用)があることを示しています。
\[\]
3水準の割り付けポイントは、2水準と同じで「主効果と交互作用、または交互作用同士が交絡しないように割り付ける」ことです。
\[\]
③実験の実施
実験しましょう
(。`・ω・)はぃ
\[\]
実験のポイントはフィッシャーの3原則です。
- 反復
- 無作為
- 局所管理
\[\]
反復については、直交配列表では組み合わせ変えて反復実験を行います。
無作為化については、直交配列表の番号順に実験を行うと結果が偏る可能性があるため、ランダムに実験を行います。
(。´・ω・)?
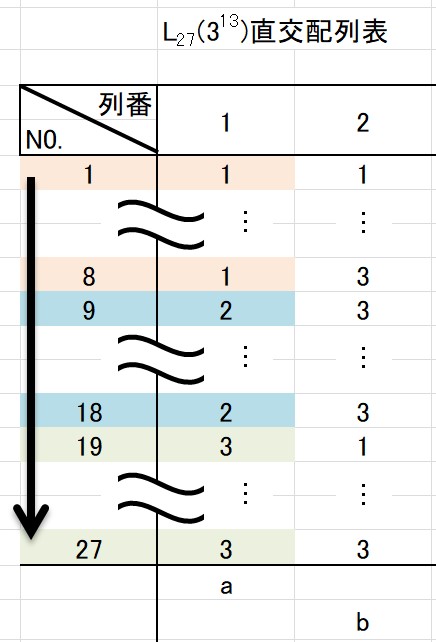
例えば番号順に実験を行った場合を考えてみましょう。
もし第1列に主効果を割り付けていたのなら、水準1の実験を全て終えてから水準2の実験を行い、水準2の実験を全て終えてから水準3の実験を規則的に実験してしまいます。
\[\]
これでは、「無作為な実験」とは言えないですよね。
くじ引きやエクセルのランダム関数などで、\(\dot{し} \dot{っ} \dot{か} \dot{り} \) ランダムに実験を行いましょう!
\[\]
最後の局所管理についてです。
実験をランダムに行いたくても、手間やコストの兼ね合いから、ある程度のグループで実験する場合があります。
そんな時の実験方法・解析方法については、局所管理の考え方で分析を行います。
別記事で解説していきます。
\[\]
④計算補助表の作成
計算補助表の作り方は2水準の時と同じになります。
水準が三つになっていることに気をつけましょう。
今回は、次の表のように結果を得られたと仮定して、計算方法を説明していきます。


ちょっと見づらいのは勘弁で!
(∵・ω・)サーセン。
\[\]
⑤列平方和の計算
3水準の直交配列実験では、第k列の列平方和\(S_{[k]}\) を次の式で求めることができます。
\[S_{[k]}=\frac{{T_{[k]1}}^2}{N/3}+ \frac{ {T_{[k]2}}^2 }{N/3} + \frac{{T_{[k]3}}^2}{N/3} -CT\]
\[\]
三つの水準に対して計算するので、分母は\(N/3\) となっていることがわかります。
交互作用を計算する場合は、二つの列平方和を足すことを忘れないようにしましょう!
\[\]
修正項(\(CT=\frac{T^2}{N}\))は、
\[ CT=\frac{T^2}{N} =\frac{238^2}{27}\]
で求められます。
分母の27 は実験回数(\(=N\))、分子の238は実験データの合計になります。
実験データの合計は、各列のデータ合計と等しくなります。
\[\]
例えば、因子Aを割り付けている第1列のデータの合計は、

\[94+87+57 \qquad = 238\]
この結果は、ほかの列でも同じ値になります。
\[\]
それでは、各列平方和を計算してみましょう。
例えば、第1列の列平方和 (\(k=1\)) は、
\[S_{[k=1]}=\frac{{T_{[k=1]1}}^2}{N/3}+ \frac{ {T_{[k=1]2}}^2 }{N/3} + \frac{{T_{[k=1]3}}^2}{N/3} -CT\]
\[= \frac{94^2}{27/3}+ \frac{87^2 }{27/3} + \frac{57^2}{27/3} – \frac{238^2}{27} \]
\[= \frac{8836}{9}+ \frac{7569}{9} + \frac{3249}{9} – \frac{56644}{27} \]
\[=981.78+841+361-2097.93\]
\[=85.85\]
\[\]
この計算を第13列まで行い、分散分析表を作成します。
ポイントは「実験データの和」と「列平方和」を混同しないことです!
実験データの和から列平方和を計算します。
(´・ω・`)ゞウーン
\[\]
⑥分散分析の実施
「⑤列平方和の計算」で各列平方和を計算できたら、分散分析を実施します。
各列平方和の自由度が2、交互作用の自由度は4であることに気をつけましょう。
\[\]
「④計算補助表の作成」の補助表に列平方和を計算した結果を加えます。

\[\]
この結果を分散分析表でまとめると…
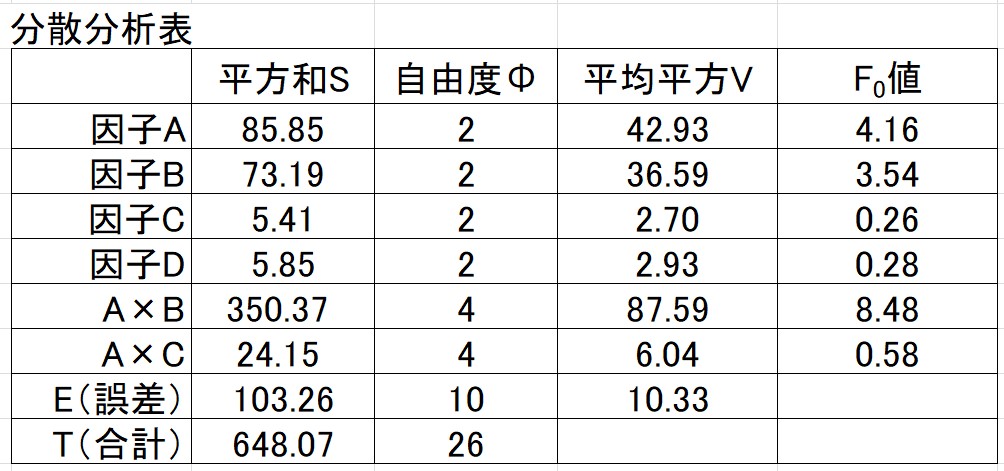
E(誤差)の平方和は、因子を割り付けていない第9列から第13列の列平方和の合計になります。
\[\]
前回と異なり、自由度が1ではありません。
そのため平方和Sを自由度Φで割って求める平均平方Vは、平方和Sとは異なります。
※前回と同様、因子毎の\(F_0\)値は、因子毎の平均平方を誤差の平均平方で割ることで求めます。
\[\]
前回 と同様に、\(F_0\)値が2以下のものはプールします。(プーリング)
すると、分散分析表は以下のようになります。
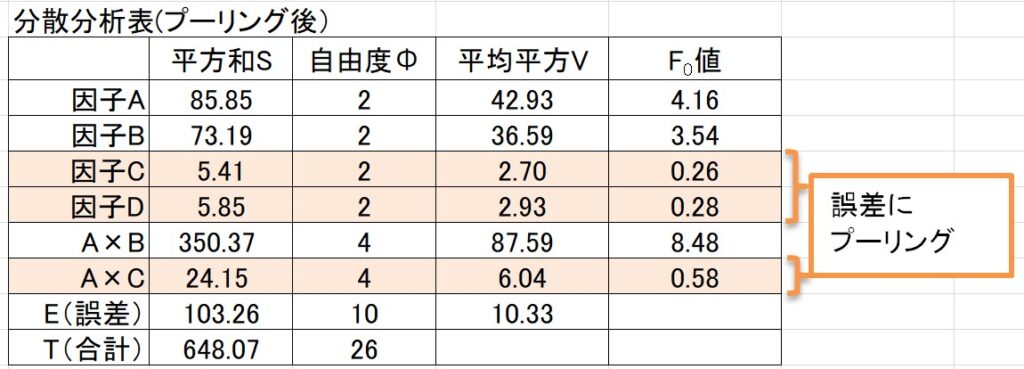
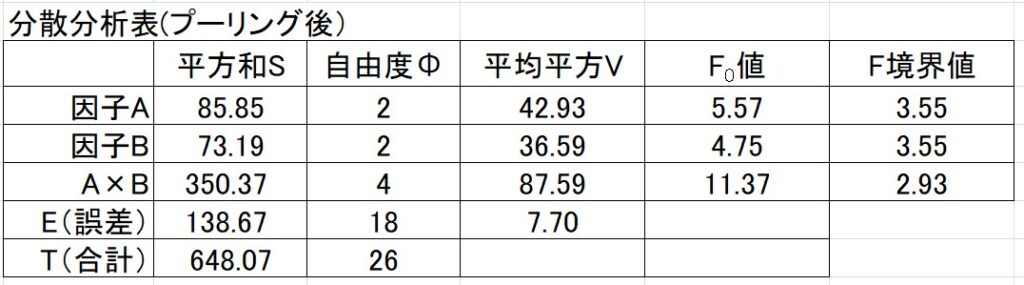
※F境界値は有意水準5%で計算しました。
因子A、因子B、交互作用A×B のいずれも、\(F_0\)値はF境界値よりも大きいです。(有意である)
分散分析表を使うところは、要因配置実験と同じですね。
分散分析表の結果から
\[\]
⑦データの構造式の確認
データの構造式や母平均の推定方法は2水準と同じです。
ただし、3水準なので分母の数字には気をつけましょう!
\(L_{27}(3^{13})\) 直交配列表 の場合、例えば次のようになります。
\[\]
①主効果A、B、C、交互作用A×B がある場合
構造式は次のようになります。
\[\hat{\mu}(ABC)=\widehat{\mu+a+b+c+(ab)}\]
\[=\widehat{\mu+a+b+(ab) } \qquad +\widehat{ \mu+c }-\hat{\mu}\]
\[=(ABの平均)+(Cの平均)-(全体平均) \]
\[=\frac{ABの水準の合計}{3}\qquad+\frac{Cの水準の合計}{9}\qquad-\frac{総計}{27}\]
\[\]
さて、分母の数字が 3, 9, 27 と3種類あります。
分母の数字が違う理由は、「対応するデータの平均値を求めているから」です。
(。´・ω・)?
もう少し詳しく考えてみましょう。
\[\]
始めに、\( \frac{ABの水準の合計}{3} \qquad \) ですが、Aの水準は3種類、Bの水準も3種類です。
AとBは交互作用があるとして考えているため、セットで考えます。
A、Bの水準で被りのない組み合わせを考えると…
\[ 3 \times 3 = 9 \]
となります。
全データ数が 27 なので、 「同じ水準の組み合わせ」は 3回出てくることになります。
※第1列に因子Aを、第2列に因子Bを割り付けました。
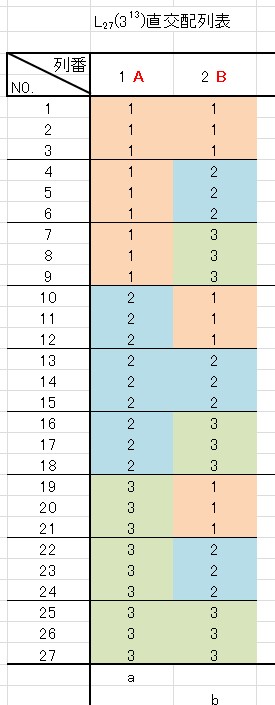
確かに、同じ水準の組み合わせは3回ずつ出ていますね。
\[\]
次に、\( \frac{Cの水準の合計}{9}\qquad \) を考えてみます。
因子Cは他の因子との交互作用がないとしています。
なので、因子Cの中で同じ水準が何回繰り返されているかに注目します。
すると、 9回 であることがすんなりわかると思います。
※第5列に因子Cを割り付けました。
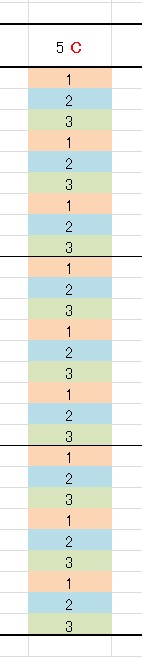
\[\]
最後に\( \frac{総計}{27} \) ですが、これはもう大丈夫ですよね。
全データ数(=実験回数) が27なので、分母が27になります。
\[\]
まとめると、分母の数字の違いは、「対応するデータの平均値を求めている」です。
\[=\frac{ABの水準の合計}{3}\qquad+\frac{Cの水準の合計}{9}\qquad-\frac{総計}{27}\]
\[\]
②主効果A、B、C、交互作用A×B、A×C がある場合
構造式は次のようになります。
\[\hat{\mu}(ABC)=\widehat{\mu+a+b+c+(ab)+(ac)}\]
\[=\widehat{\mu+a+b+(ab)} \qquad +\widehat{ \mu+a+c+(ac) }-\widehat{\mu+a}\]
\[=(ABの平均)+(ACの平均)-(Aの平均) \]
\[=\frac{ABの水準の合計}{3}\qquad +\frac{ACの水準の合計}{3}\qquad -\frac{水準Aの合計}{9}\]
\[\]
因子Aが重複しているので、最後の項でマイナスするのは\(\frac{水準Aの合計}{9}\) であることに気をつけましょう。
分母の数字が 3 と 9 があります。
もう大丈夫ですよね。
( ゚ 3゚)~♪
\[\]
最初の2項は、因子Aと因子B、因子Aと因子Cで交互作用を考えているため、3 となります。
最後の項は、因子Aが3水準であり、全データ数が27であることから、
\[\frac{27}{3} = 9\]
となります。
\[\]
⑧最適条件における母平均の推定
母平均の推定方法も2水準の推定と基本は同じになります。


「⑦ データの構造式の確認 」で分解した構造に、最適水準の結果を当てはめれば完成です。
\[\]
例えば、因子A、B、Cと交互作用A×Bがある場合の3水準直交配列実験で考えてみます。
最適水準は、二元表(交互作用A×B)より \(A_2B_1\)、計算補助表より \(C_3\) となります。
\[\]
因子Aと因子Bの最適水準は、計算補助表をみるとともに水準1の合計が一番高いです。
しかし、交互作用があるため、二元表より最適水準を選んでいます。
\[\]
\[\hat{\mu}(A_2B_1C_3)=\widehat{\mu+a_2+b_1+c_3+(ab)_{21}}\]
\[=\widehat{\mu+a_2+b_1+(ab)_{21} } \qquad +\widehat{ \mu+c_3 }-\hat{\mu}\]
\[=\frac{A_2B_1の水準の合計}{3}+\frac{C_3の水準の合計}{9}-\frac{総計}{27}\]
※先の例では、因子Cは誤差としていますが、解説のため入れています。
\[\]
\[=\frac{A_2B_1の水準の合計}{3}+\frac{C_3の水準の合計}{9}-\frac{総計}{27}\]
\[=\frac{51}{3}+\frac{85}{9}-\frac{238}{27}\]
\[=17+9.44-8.81 \qquad = 17.63\]
\[\]
次に有効反復係数\(n_e\) を計算すると、
\[n_e=\frac{総データ数}{1+自由度の和}\]
\[=\frac{27}{1+2+2+4+2}\]
\[=\frac{27}{11}\]
自由度の和は「因子Aの自由度(2)+因子Bの自由度(2)+交互作用A×Bの自由度(4)+因子Cの自由度(2)」からなります。
\[\]
信頼率95%で区間推定を計算すると、
\[ \hat{\mu}(A_2B_1C_3) \pm t(18,0.05)\sqrt{\frac{V_E}{n_e}}\]
\[17.63 \pm t(18,0.05)\sqrt{\frac{11}{27}\times 7.70} \]
\[=17.63 \pm 2.101 \times 1.771\]
\[=17.63 \pm 3.721\]
\[=13.91,21.35\]
※\(V_E\) は分散分析表より、 7.70 です。
\[\]
2水準の直交配列実験と同様に、最適水準は実験していない可能性があります。
最適水準を求めたら、最適水準で検証しましょう!
\[\]
⑨母平均の差の推定
母平均の差の推定については、2水準の場合と同じになります。
\[\]
各水準について信頼率95%で区間推定を行うと、信頼区間は2水準と同じく次の式で求まります。
\[\hat{\mu}(A_1B_1C_1)\pm t(\phi_E,0.05)\sqrt{\frac{V_E}{n_e}}\]
※上式では因子A、因子B、因子Cの水準が1の場合の計算になります。
計算方法の詳細は、記事「直交配列実験とは 2 2水準」をご参照ください。
\[\]
2水準と同様に、水準間の差の信頼区間を計算してみましょう。
例えば、すべての水準が1の時とすべての水準が2の時の差の信頼区間は次のようになります。
\[\{\hat{\mu}(A_1B_1C_1)- \hat{\mu}(A_2B_2C_2) \}\pm t(\phi_E,0.05)\sqrt{\frac{2}{n_e}V_E}\]
やはり、2水準間の計算と同じになります。
|・ω・)フムフム
\[\]
⑩最適水準におけるデータの予測
2水準と同じ計算式で求められます。
すべての因子の最適水準が、水準1の「信頼率95%の区間予測の式」は次のようになります。
\[\hat{\mu}(A_1B_1C_1)\pm t(\phi_E,\alpha)\sqrt{\left( 1+\frac{1}{n_e}\right)V_E}\]
\[\]
予測区間は信頼区間とは異なるので、気をつけましょう
詳細は記事「 直交配列実験とは 2 2水準 」をご参考ください。
\[\]
まとめ
①3水準の直交配列実験では、2水準の直交配列実験よりかなり増える
②3水準の直交配列実験では、交互作用は2列に表れる
③実験はランダムに行う
④計算補助表は、実験データを列番毎にまとめる(または二元表)
⑤列ごとに列平方和を計算する(実験データの和と列平方和を混同しない!)
⑥誤差に入れれそうな因子や交互作用は、誤差にプーリング
⑦データの構造式から推定値の計算式を導く
⑧母平均の推定は \(\hat{\mu}(ABCD)\pm t(\phi_E,\alpha)\sqrt{\frac{V_E}{n_e}}\)
⑨母平均の差 を推定すれば、水準を変えるべきか判断できる
⑩予測値 ≠ 推定値
\[\]
前回の記事「 直交配列実験とは 2 2水準 」と内容が重なっているところは、説明を割愛しました。
3水準間の直交配列実験ならではの特徴を理解しましょう!
\[\]















[…] 前回(直交配列実験とは 2 2水準)、前々回(直交配列実験とは 3 3水準)の記事で学んだ、2水準法と3水準法についてまずは復習です。 […]