直交配列実験とは 1 基本編
公開日2021年12月15日 最終更新日 2022年3月5日
みなさんこんにちは、michiです。
今回から数回に分けて、直交表について学んでいきます。
QC検定1級での出題頻度が高く、実践的な内容なのでしっかりと理解しましょう!
キーワード:「直交配列表」

目次
①直交表(直交配列表) とは
直行表とは部分配置実験において、因子を割り付けるために使う表のことです。
(。´・ω・)?
直行表は水準の数と要因の数、交互作用の数で使う表が変わります。
例えば、2水準系直行配列表\(L_8(2^7)\) は次の表を使います。
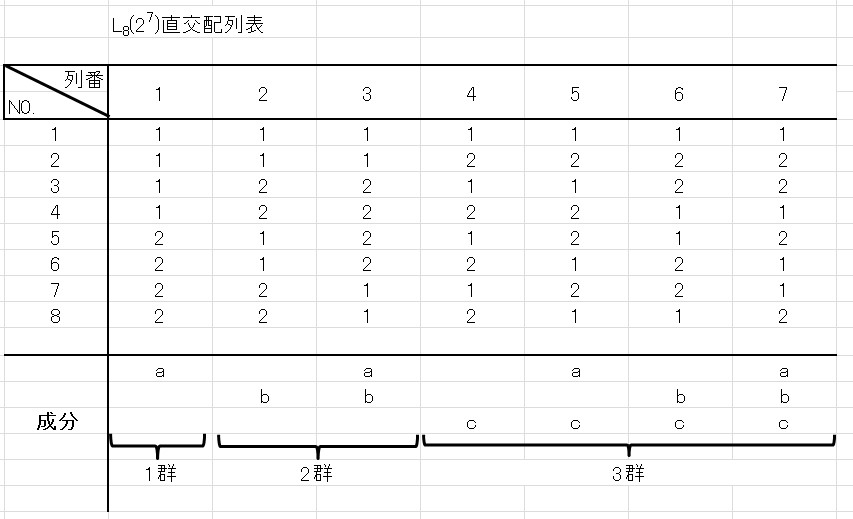
この直行表には「成分」と書かれている項目があります。
この成分を見ながら、交互作用のあるものは交互作用にあたる列を割り付けます。
\[\]
②要因配置実験との違い
記事「実験計画法1 一元配置実験」と「 実験計画法1 二元配置実験 」では、一元配置実験と二元配置実験を学びました。
一元配置実験と二元配置実験は「要因配置実験」と言い、すべての組み合わせの実験を行う必要があります。
例えば、3つの因子がそれぞれ3水準ある場合は、\(3^3=27\) 通りの実験をする必要があります。
交互作用を考慮する場合は、2回以上繰り返さなくてはいけないので、\(27 \times 2 =54\)回実験が必要です。
\[\]
一方、すべての水準組み合わせを実験せずに、一部の水準組み合わせのみを実験する方法を「部分配置実験」と言います。
すべての組み合わせを行わなくても、最も効果の高い水準を選択することができるんです!
Σ(・ω・ノ)ノ!
\[\]
部分配置実験では、要因配置実験よりも少ない実験回数で済むので、効率的で実践的な手法になります。
\[\]
③直交表のミカタ
先ほどの 2水準系直交配列表\(L_8(2^7)\) を使って部分配置実験を考えてみます。
まず「 \(L_8(2^7)\) 」 の意味ですが、2水準の因子に対し8回実験を行い、最大7つの要因まで分析できるということを表します。
(。´・ω・)?
\[\]
例えば、2水準の因子\(A\),\(B\),\(C\)があり、交互作用\(A\times B\), \(A\times C\) があるとします。
各列番に各要因を割り付けるとします。
割り付け方法はいくつか考えられますが、「列番1にA、列番2にB、列番4にC」を割り付けたとします。
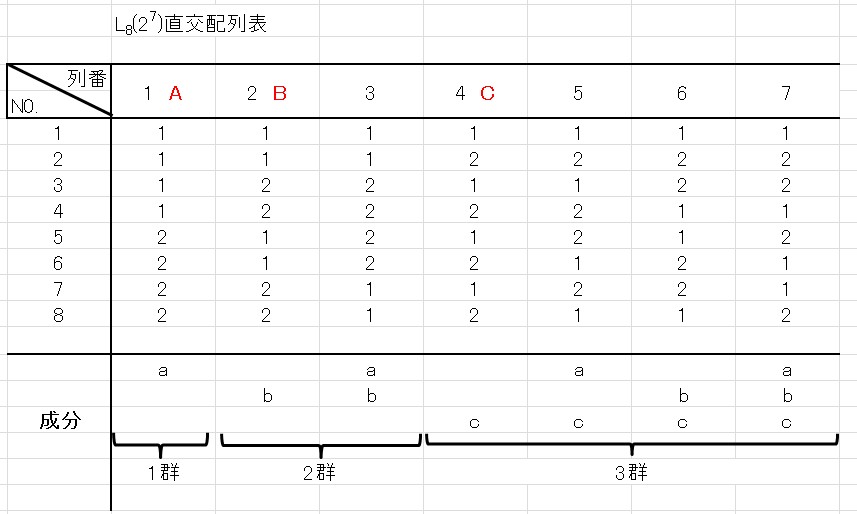
直行表の列番とNo.以外には、「 \(1\) 」か「 \(2\) 」の数字が書かれています。
これは、2水準の直交表なので 「 \(1\) 」か「 \(2\) 」 が書かれているわけです。
割り付けられた直交表に従うと、因子Aは実験No.1~4は水準1で、実験No.5~8は水準2で行うことになります。
因子Aが水準1で実験されるとき、列番2に割り付けられた因子Bと列番4に割り付けられた因子Cを見てみましょう。
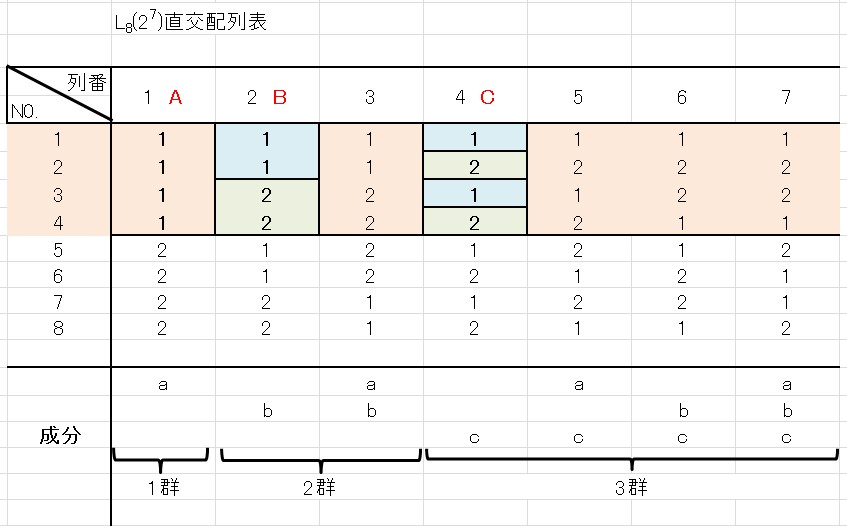
因子Aにおける4回の水準1の実験で、因子B・因子Cそれぞれ水準1と水準2が2回ずつあることがわかります。
この状況は因子Aの水準2の4回の実験でも同じです。
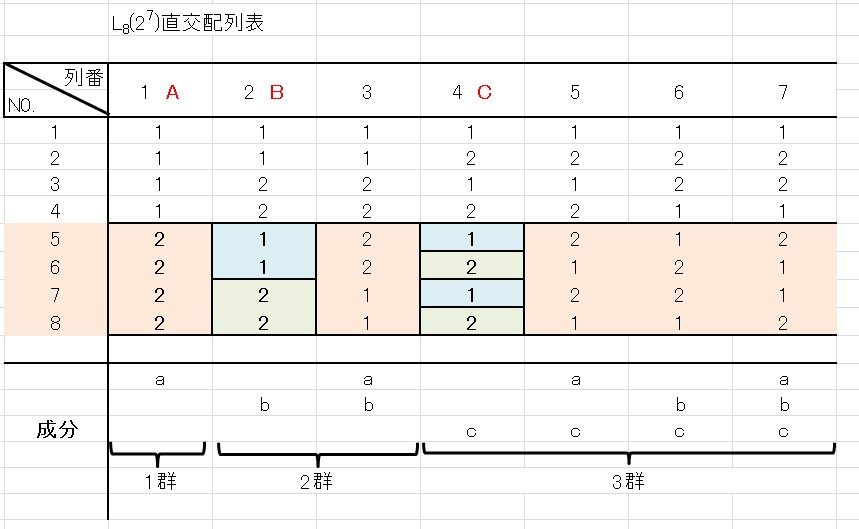
\[\]
直交表ではある因子の特定の水準に対し、ほかの因子の水準は同じ回数だけでるように調整されています。
ほかの因子の水準が同じ回数でるということは、ほかの因子の影響を平等に受けることになります。
そのため、因子Aの水準1と水準2の比較を行う場合は、実験No.1~4の結果と実験No.5~8の結果を比較すればよいことになります。
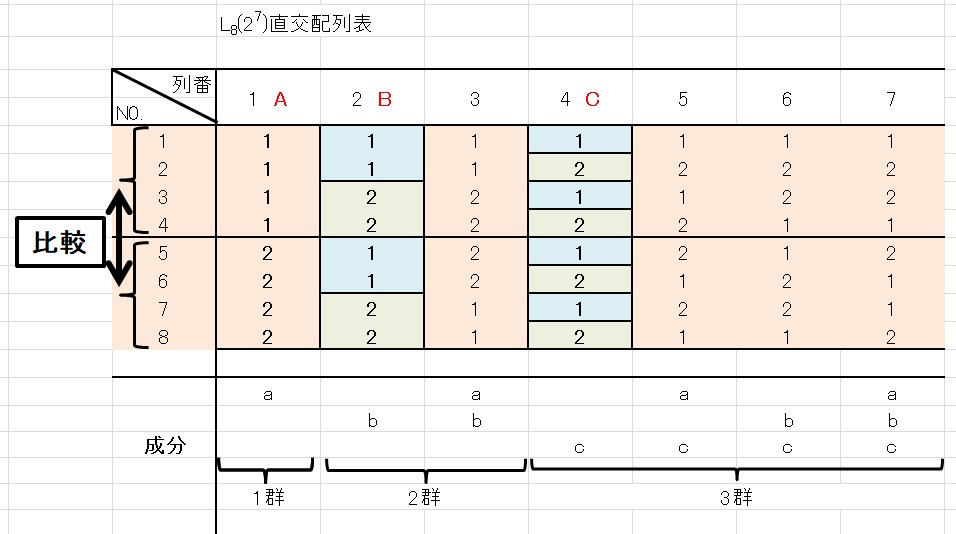
\[\]
④直交表への割り付け
直交表の列番に各因子を割り付ける方法は主に2つあります。
- 成分を利用
- 線点図を利用
適切な割り付けができないと、交絡してしまいます。
交絡すると、分析した結果が割り付けた要因によるものなのか、交互作用によるものなのか判断ができなくなってしまいます。
(´・ω・`;)
\[\]
①成分を利用
\(L_8(2^7)\) 直交表を見てみましょう。

直交表の下の方に成分の欄があり、アルファベット(a,b,c)が書かれています。
このアルファベットを頼りに、交絡しないように割り付けを行います。
\[\]
今回の例では、列番1に「a」、列番2に「b」と書いてあり、因子Aを列番1に、因子Bを列番2に割り付けています。
因子Aと因子Bに交互作用がある場合は、列番3に交互作用が現れます。
列番3の成分を見ると、「ab」と書かれています。
( ゚д゚)ハッ!
そうです。
列番1の成分「a」と列番2の成分「b」をかけ合わせた「ab」が列番3の成分です。
もし、因子Aと因子Bに交互作用がないことが明確であるならば、列番3に他の因子を割り付けることができます。

ポイントは交互作用のでる列番に他の因子を割り付けないことです。
繰り返しになりますが、交互作用があるのに他の因子を割り付けると、交絡が発生するためです。
\[\]
因子Cを列番6に割り付けた場合を考えてみましょう。
因子Aと因子Cに交互作用がある場合は、先ほどと同様に考えます。
因子Aの列番1の成分「a」と因子Cの列番6の成分「bc」をかけ合わせると、成分「abc」となります。
成分「abc」は列番7が当てはまります。
よって、交互作用A×Cは、列番7に現れます。
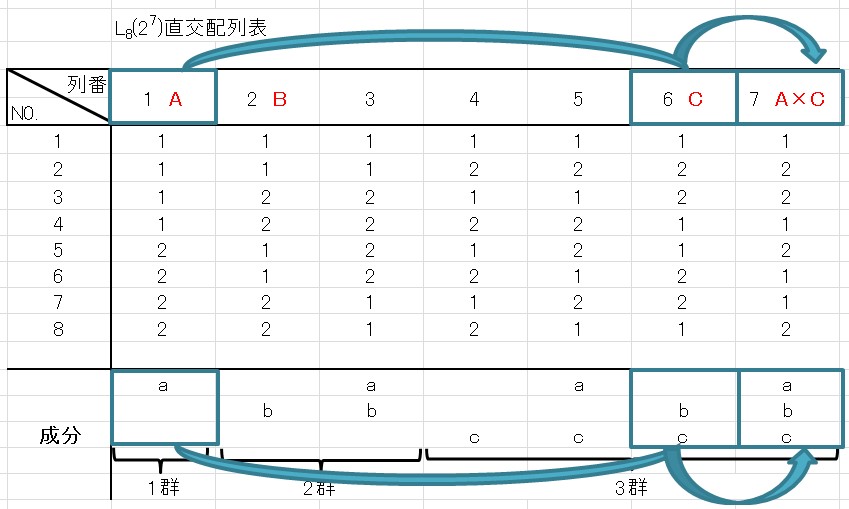
\[\]
では、因子Bと因子Cの交互作用はどこに現れるのでしょうか?
(。´・ω・)?
成分で考えてみましょう。
因子Bは列番2で成分は「b」、因子Cは列番6で成分は「bc」なので、かけ合わせると、「b\(^2\)c」となります。
しかし、成分「 b\(^2\)c 」なんてものはありません!
(;’ω’∩)
\[\]
2水準の直行表では、”二乗した成分は「 1 」にする”というルールがあります。
つまり、成分 「b\(^2\)c」⇒「1×c」⇒「c」 となるわけです。
成分「c」は列番4が当てはまるので、因子Bと因子Cの交互作用B×Cは列番4に現れます。
\[\]
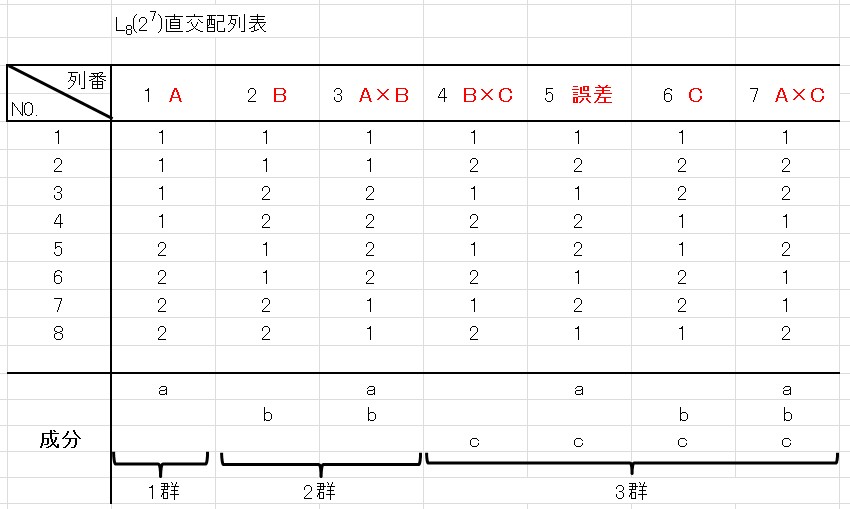
これまでの割り付けた情報を直交表に当てはめると、下図のようになります。
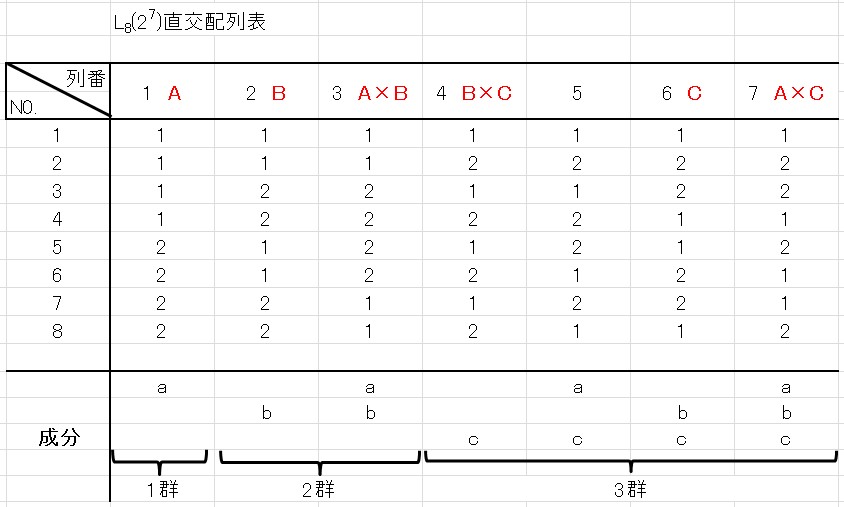
\[\]
列番5の成分「ac」が余っています。
この列番5が誤差を表す列になります。
要因配置実験でも誤差を考えましたよね。
\[\]
今回は \(L_8(2^7)\) 直交表 を例として説明しました。
因子の数が増える場合は、 \(L_{16}(2^{15})\) 直行表など、より多くの因子を割り付けできる直交表を選びましょう。
\[\]
②線点図を使用
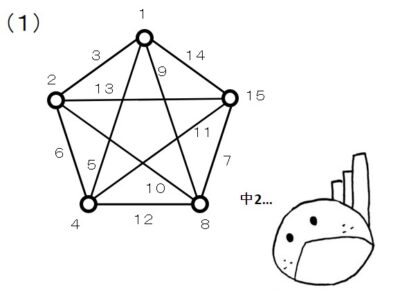
線点図とは、次の図で表されるものです。
※\(L_8(2^7)\) の場合は二つあります。
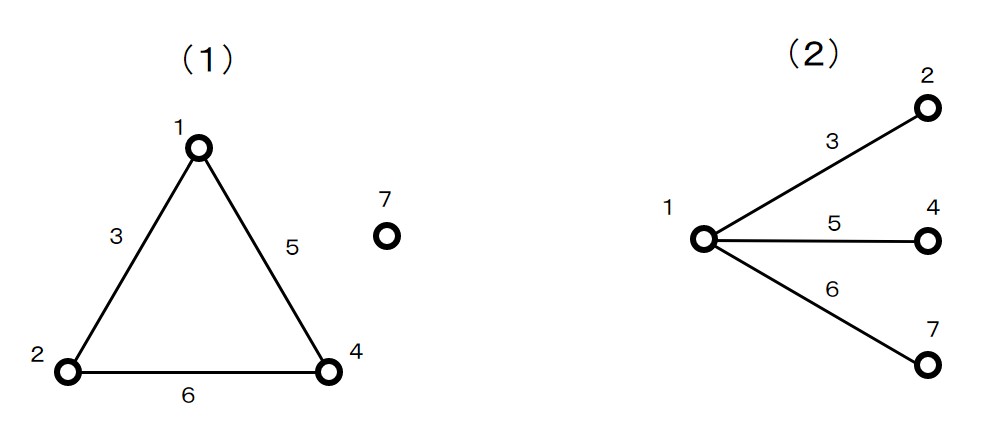
線と点に数字が書かれています。
この数字が直交表の列番にあたります。
点を結ぶ線の数字が、交互作用が表れる列番号になります。
\[\]
例えば、因子A、B、Cを考えてみましょう。
線点図(1)に、因子Aを点1、因子Bを点2、因子Cを点4に割り付けます。
線点図から、交互作用A×B、交互作用A×C、交互作用B×C、 はそれぞれ、線3、線5、線6に表れます。
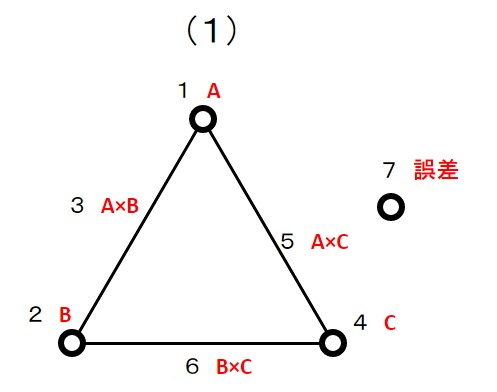
このとき、使用していない点7が誤差を表します。
この結果を直交表の成分で確認してみましょう。
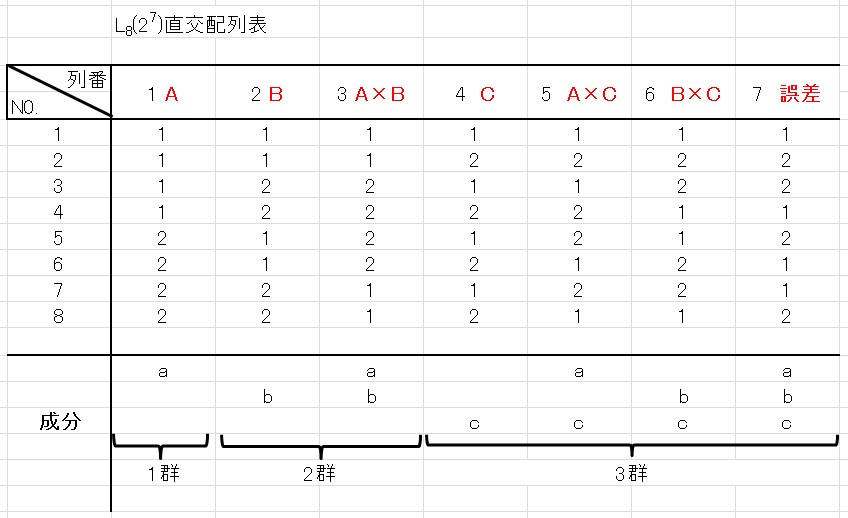
成分を見ても矛盾がなく、いい感じですね。
(・ω・)bグッ!
\[\]
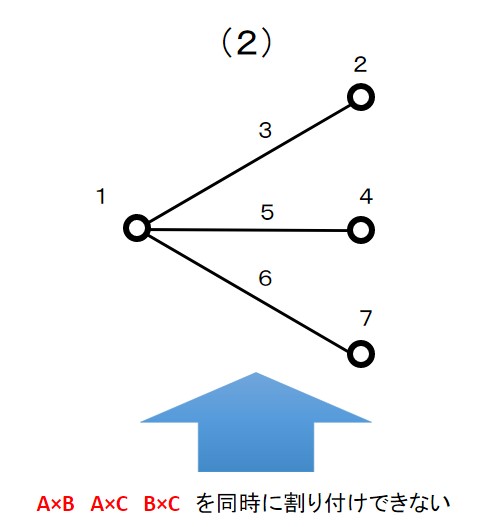
なお線点図(2)は、交互作用A×B、交互作用A×C、交互作用B×C を全て考える場合は、使用できません。
三つの交互作用を同時に割り付けられる線がないためです。
\[\]
さて、因子の数を増やして、 \(L_16(2^15)\) の線点図を見てみましょう。
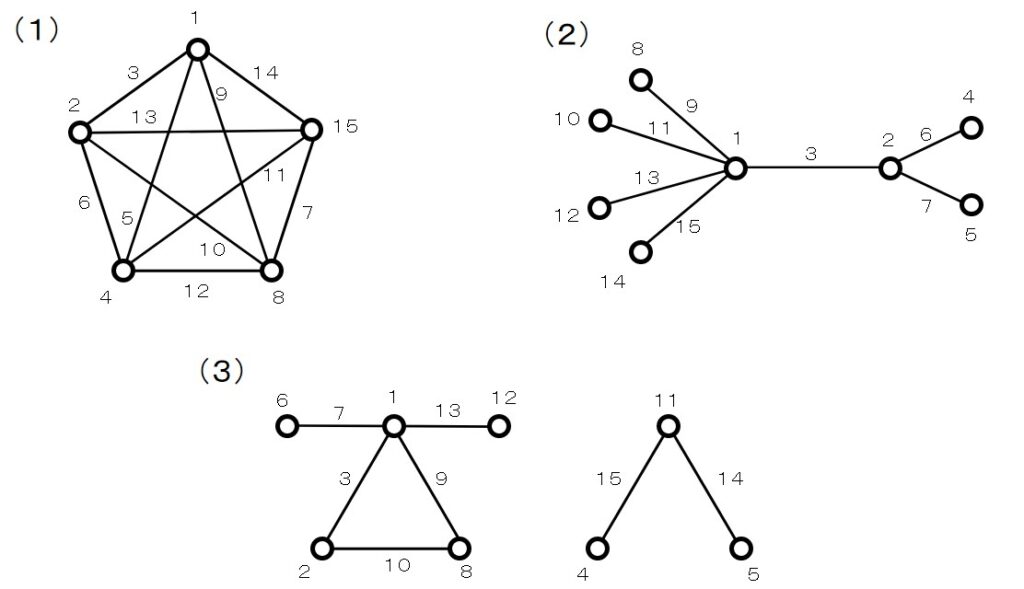
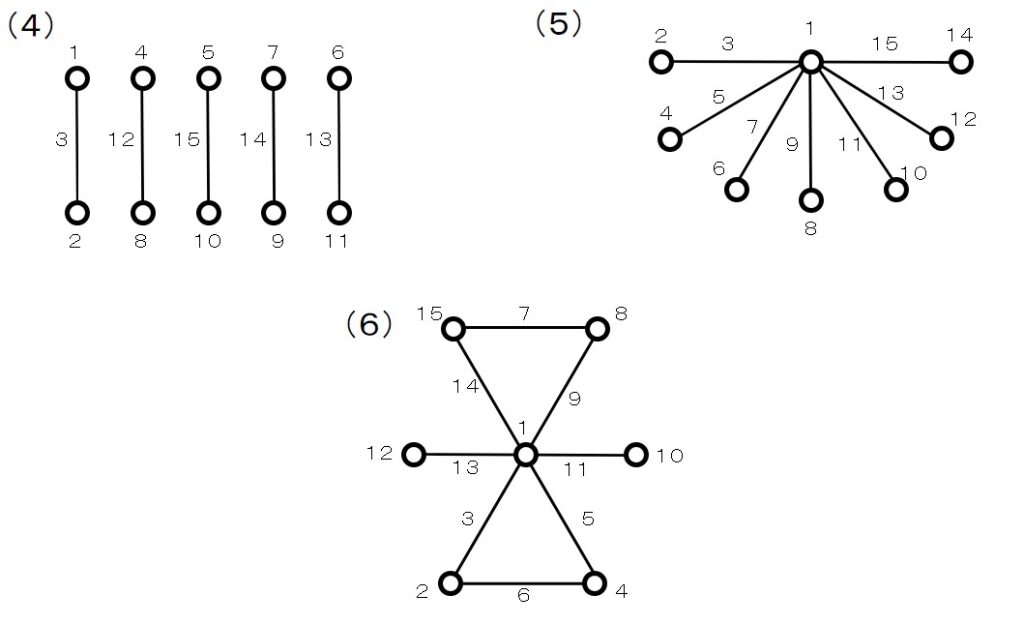
\(L_{16}(2^{15})\) の線点図はいろいろな種類がありますね。
この中でも一番 中二病心 を刺激するこいつで行きましょう。
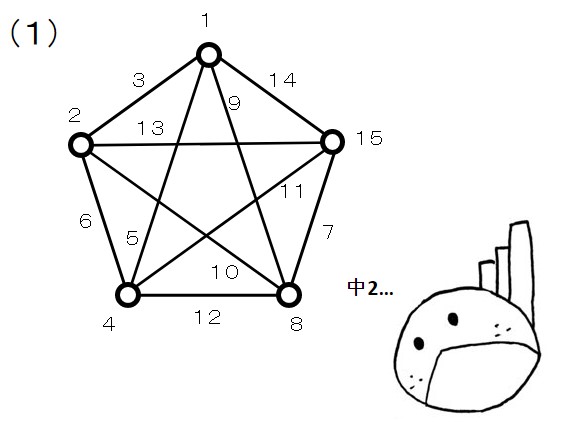
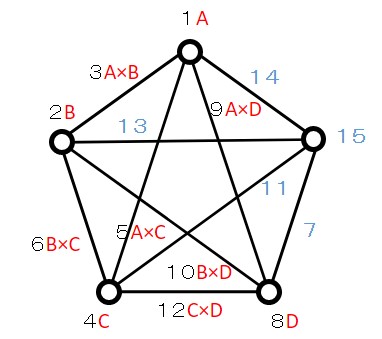
因子A、B、C、Dがあり、すべての因子間で交互作用があるとします。
点1、2、4、8に因子A 、B、C、D を割り付けると、各交互作用が表れる列番は下表のようになります。

このとき、使っていない線や点(7,11,13,14,15)は、誤差を表す列番になります。
\[\]
他の線点図でも考えてみましょう。
砂時計型のこいつを使います。
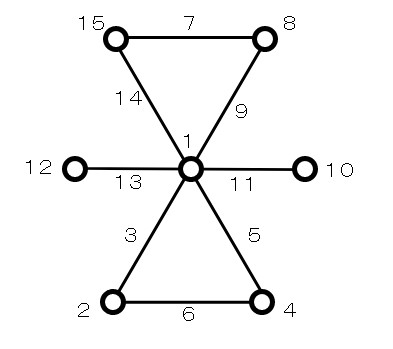
点1、2、4、8に因子A 、B、C、D を割り付けます。
各線が交互作用を表すので、交互作用が表れる列番は次の表のようになります。

このときの線点図は次のようになります。
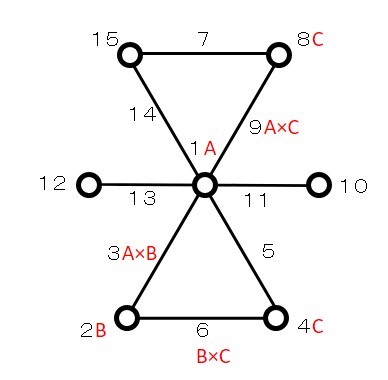
ポイントは、因子Bと因子D、因子Cと因子Dの交互作用が表す線がないことです。
これでは、交互作用B×Dと交互作用C×Dの表れる列番がわかりません!
どうすればよいのでしょうか?
(。´・ω・)?
答えは、「砂時計型の線点図を使用しない」です。
考えるべき交互作用を表すことができる線点図を使いましょう!
\[\]
まとめ
①直交表は部分配置実験で因子を割り付けるのに使う
② 全てのパターンの実験をするのが要因配置実験、できるだけ少ない実験数が部分配置実験
③割り付けは成分を使うか、適切な線点図を使う
\[\]
割り付けの方法がわかったので、次回からは直行配列表実験について計算方法を学んでいきましょう!
\[\]














[…] 前回に引き続き、今回も直交表について学んでいきます。 […]