公開日2020年2月9日 最終更新日 2022年4月2日
みなさんこんにちは、michiです。
前回の記事で不偏分散の計算方法とその意味をまなびました。
不偏分散をまなぶことで、サンプル数が異なっていても「ばらつき」を評価できるようになったのに、なぜ標準偏差を考える必要があるのでしょうか?
それは、測定値と次元が違うからです。
(。´・ω・)?
どういうことか、学んでいきましょう!
キーワード: 「標準偏差」
\[\]
目次
①標準偏差とはなにか
標準偏差は、次の式で表されます。
\[ 標準偏差 = \sqrt {不偏分散} \]
簡単ですね。
標準偏差は、不偏分散の平方根(√ ルート)になります。
\[\]
こんな簡単な計算なら、不偏分散のままでよい気もしますが、平方根をとる理由があります。
それは、冒頭にも書きましたが、「次元が違うから」です。
(。´・ω・)?
\[\]
どういうことでしょうか?
不偏分散は平方和を自由度で割って求めました。
その平方和は、測定値と平均からのずれを二乗した合計でした。
そうです、二乗してしまったため、不偏分散と平方和は、本来のデータの次元より一つあがってしまうのです!
\[\]
次の例を考えてみましょう。
ある生産ラインで作られている製品の「長さ」の「ばらつき」を評価します。
ばらつきを評価するために、平方和を計算し、不偏分散を求めました。
\[\]
しかし、得られた不偏分散は、「長さ」を二乗して計算した値ですので、「面積」の単位になります。
これでは、「長さ」のばらつきを評価していることにはなりません・・・
(;´・ω・)
\[\]
②標準偏差を考える理由
平方和や不偏分散では、ばらつきの単位が異なることがわかりました。
そこで、標準偏差(=不偏分散の平方根)を考えるのですが、その前に問題です。
問)「ばらつき」の単位はなんでしょうか?
(。´・ω・)?
\[\]
答えは、 何の「ばらつき」を見ているかにより変わる です。
テストの点数では「点」ですし、長さなら「メートル」や「ヤード」かもしれません。
「ばらつき」は評価しようとするデータの単位に依存します。
\[\]
つまり「ばらつき」の値を単位を考慮して評価するのであれば、測定値や見たいデータの単位に合わせる必要があります。
先ほどの例では、「長さ」の不偏分散が「面積」の単位になっているため、不偏分散のみでは、「長さ」の「ばらつき」の値を求めることができません。
このような背景から、測定値の「ばらつき」の値を求めるために、標準偏差を考え、単位の次元をそろえるのです。

③標準偏差が小さくなればOK?
標準偏差の意味や考え方がわかってきましたね。
では、次のグラフ1とグラフ2を見比べてください
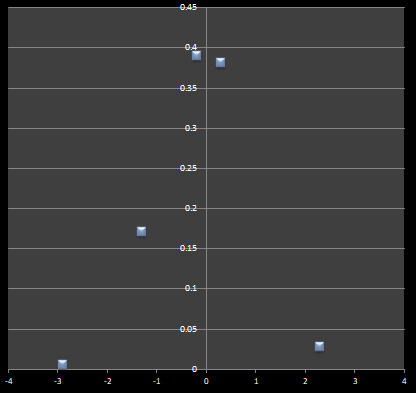
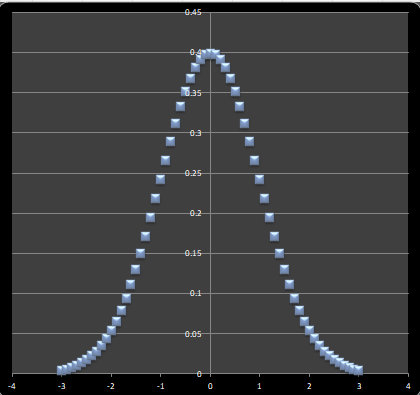
二つのグラフを見比べると、グラフ1よりもグラフ2の標準偏差が小さくなっています。
つまり、グラフ2のほうが「ばらつき」は小さくなった! と考えられそうです。
ところが、実はどちらも元データは同じなのです。
Σ(・ω・ノ)ノ!
\[\]
グラフ1のデータはグラフ2のデータから5点を抽出しただけです。
つまり、数字上は確かに「ばらつき」は小さくなっていますが、実はただデータ点数が違うだけで、同じものを表しているわけです。
このように、測定データの評価を単純に標準偏差のみで考えると、誤った答えをだす可能性があるので気を付けましょう!
では、どう評価すればよいのか?については、別の記事「検定とは」や各推定の記事で解説します。
\[\]
④標準偏差のもうひとつの意味
標準偏差の意味と注意点を学びました。
ここでもう一つ、重要な性質があります。
それは、「平均値から標準偏差だけ離れた値は変曲点になる」ということです。
┐(´∀`)┌
\[\]
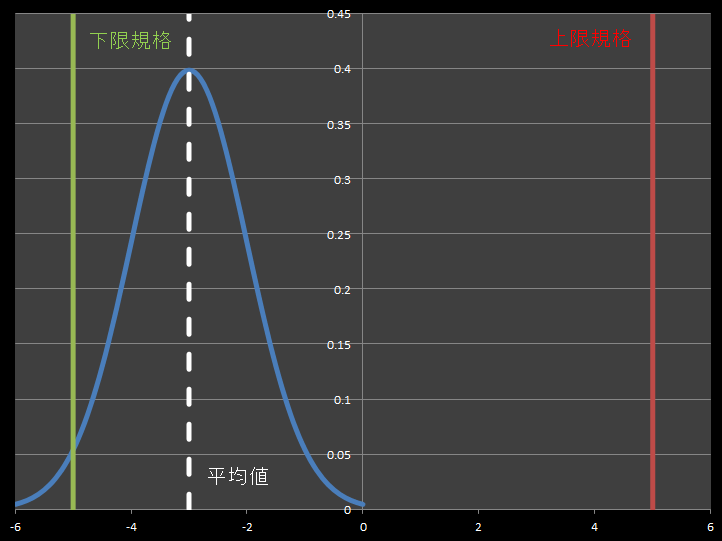
一般的に製品の分布特性は正規分布することが多いです。
イメージとしては、目標値を中心値として裾が広がったような形になります。(下図)

\[\]
この正規分布をよく見ると、中心付近は「上に凸の曲線」で、中心から外れると「下に凸の曲線」となっていることが分かります。
では、正規分布に中心値(平均値)から標準偏差だけ離れた点にマークをしてみます。

グラフが「上に凸の曲線」から「下に凸の曲線」に変わる変化点を変曲点と言います。(下に凸⇒上に凸 も変曲点)
すると、なんとこの変曲点はグラフの中心値から標準偏差(\(σ\))離れた点になるのです!
この性質は、「工程能力指数」の理解を深めていくうえで重要になってきます。
\[\]
まとめ
①\( 標準偏差 = \sqrt {不偏分散} \)
②ばらつきの値を求めるために、不偏分散ではなく標準偏差を考える
③標準偏差が小さくなったからといって「ばらつき」が小さくなったとは言えない
④平均値から標準偏差だけ離れた値は変曲点になる
\[\]
次回の記事では標準偏差を利用する統計量、変動係数について勉強していきましょう!












[…] 次回の記事では、不偏分散から標準偏差について勉強していきましょう! […]
[…] 前回の記事では、標準偏差とその意味をまなびました。 […]
[…] この答えのヒントは、記事「不偏分散ではだめ?なぜ標準偏差」に書かれています。 […]
[…] ここで分母の「(σ)」 ですが、記事「不偏分散ではだめ?なぜ標準偏差?」を参考にすると下図を見つけられます。 […]
[…] 標準偏差は、不偏分散の平方根でした。※詳細はこちら […]
[…] ここで分母の「(σ)」 ですが、記事「不偏分散ではだめ?なぜ標準偏差?」を参考にすると下図を見つけられます。 […]
[…] 「不偏分散ではだめ?なぜ標準偏差?」 […]