直交配列実験とは 4 多水準法

公開日2022年3月17日 最終更新日 2022年4月29日
みなさんこんにちは、michiです。
前回までは2水準系、3水準系の直交配列実験について学びました。
今回は多水準法について学んでいきます。
キーワード:「多水準法」

目次
①多水準法とは
前回(直交配列実験とは 2 2水準)、前々回(直交配列実験とは 3 3水準)の記事で学んだ、2水準法と3水準法についてまずは復習です。
2水準法ではすべての因子が2水準でした。
(2水準とは、比較したい条件が2つある状態です。)
3水準法ではすべての因子が3水準法でした。
φ(・ω・ )フムフム…
\[\]
実践的には、4水準の因子を考えたり、2水準の因子と3水準の因子が組み合わせで実験する場合が考えられます。
今回から、2水準法や3水準法では取り扱わない水準数に対して、考えていきます。
- 多水準法:4水準の因子を2水準の直交配列表に割り付ける
- 凝水準法:2水準の因子を3水準の直交配列表に割り付ける
今回の記事では「多水準法」について学んでいきます。
\[\]
②多水準法の手順
多水準法における分析の手順は2水準直交配列実験や3水準直交配列実験と同じになります。
ただし、割り付け方法に注意が必要になります。
Σ(・ω・ノ)ノ!
そこのところを解説していきます。
\[\]
③多水準法の割り付け
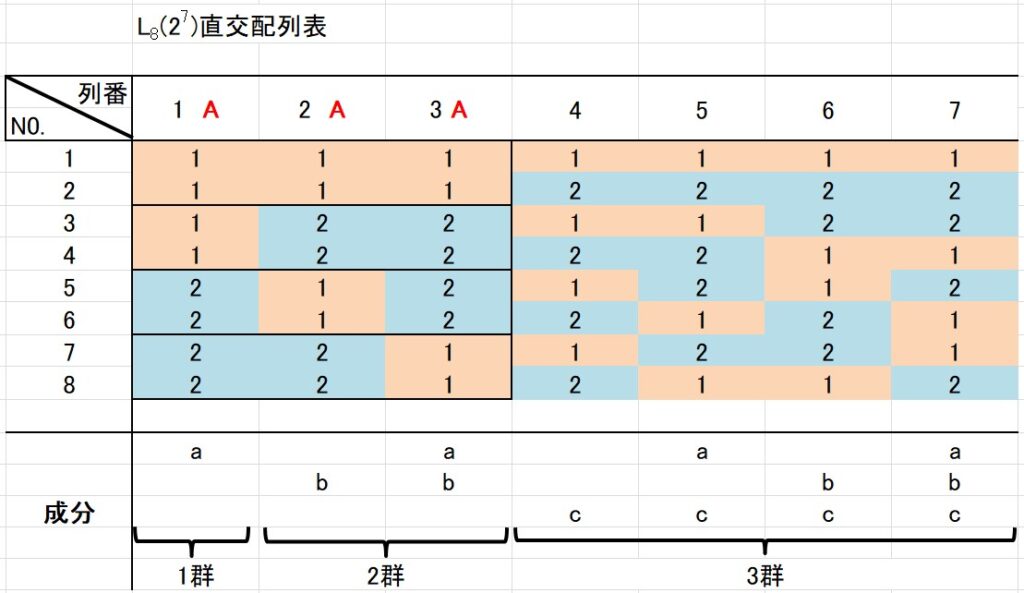
2水準の直交配列表に4水準因子を割り付ける場合は、2つの水準を組み合わせて4水準とします。
\(L_8(2^7)\) 直交配列表の1つの列を見ると、水準1と水準2が同数あります。
ほかの列を見ても、やはり水準1と水準2が同数あります。
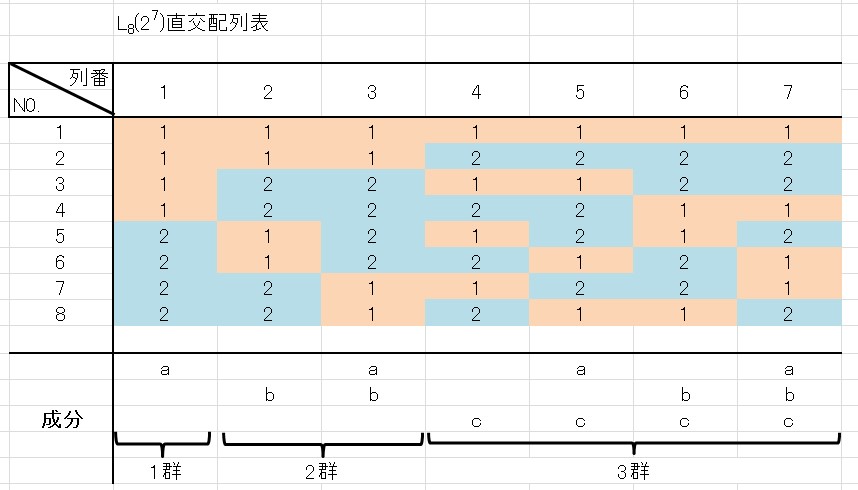
2水準の直交配列表なので当たり前ですよね。
((。 ・ω・)(。 -ω-)ぅんぅん
\[\]
2水準の直交配列表に4水準を割り付けるためには、2つの列の水準同士を組み合わせて新しい水準を作ります。
例えば、下のような組み合わせが考えられます。
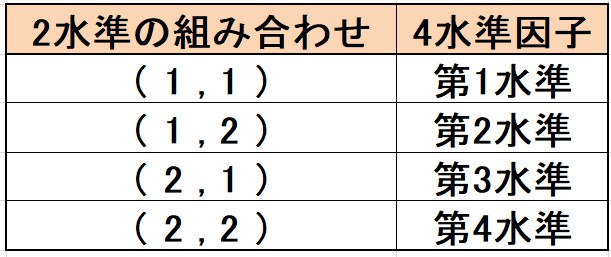
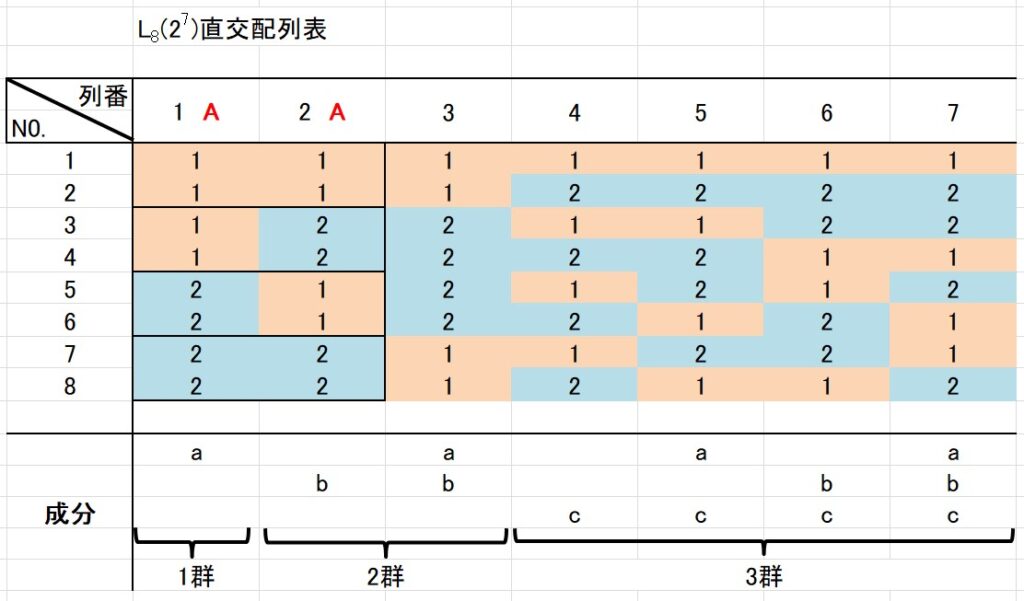
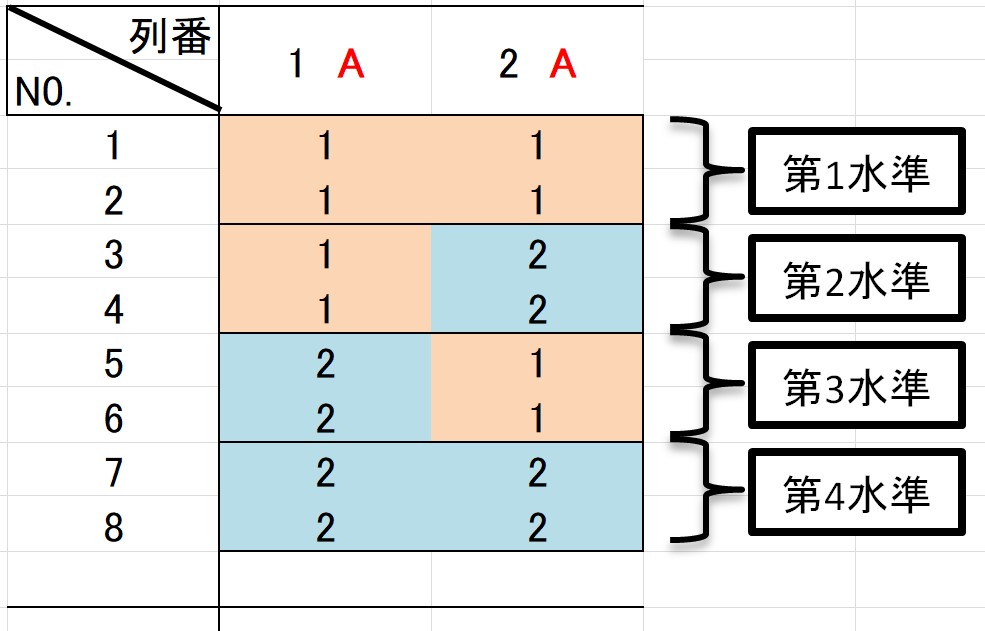
例えば、第1列と第2列を使った場合を考えてみましょう。
第1列の水準が1、第2列の水準が2の場合は、4水準因子の第2水準を表します。
\[\]
④多水準法で使用する列
多水準法で使用する列は、交互作用に該当する列も使います。
(。´・ω・)?
2水準の直交配列表では1つの列の自由度は 1 です。
因子は2水準なので列の自由度は 1 になります。
\[\]
4水準の因子の場合は自由度は 3 (=4-1) となります。
2つの列を割り付けても自由度は 2 なので、自由度が1つ足りません!
(;´・ω・)
そこでどうするかと言うと、交互作用に該当する列も使います。
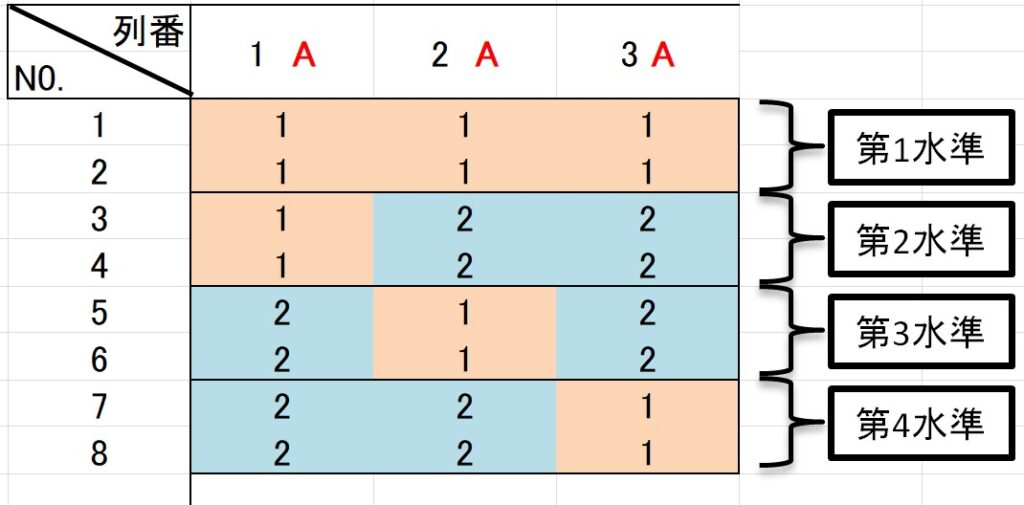
先ほどの割り付けを例にすると、以下のようになります。
第1列(成分a)と第2列(成分b)を4水準の因子の割り付けた場合、列3(成分ab)も使います。
これで列平方和の自由度 3 を確保できました!
この時、割り付けに3列使っていますが、水準の組み合わせは 4種類 しかできません。
\[\]
もし4水準因子と2水準因子で交互作用がある場合は、交互作用の自由度は 3×1 =3 なので、4水準因子と同様に3列使うことになります。
多水準法では、割り付ける列は増えますが、列平方和の計算方法は2水準直交配列実験と同じになります。
それでは、例題を参考に解いてみましょう。
(*`・ω・)ゞ了解
\[\]
⑤ 多水準法での平方和
今回は交互作用がある例で考えてみます。
因子Aを4水準、因子Bを2水準、因子Cを2水準とし、交互作用A×B、交互作用A×Cがあるとします。
交互作用の表れる列は、使用している列のかけ算分必要になります。
因子Aで3列、因子Bで1列使っているため、交互作用A×Bは3列必要です。
先ほど使用した、 \(L_8(2^7)\) 直交配列表 では数が足りません!
(・ω・`;)ノぁゎゎ
\[\]
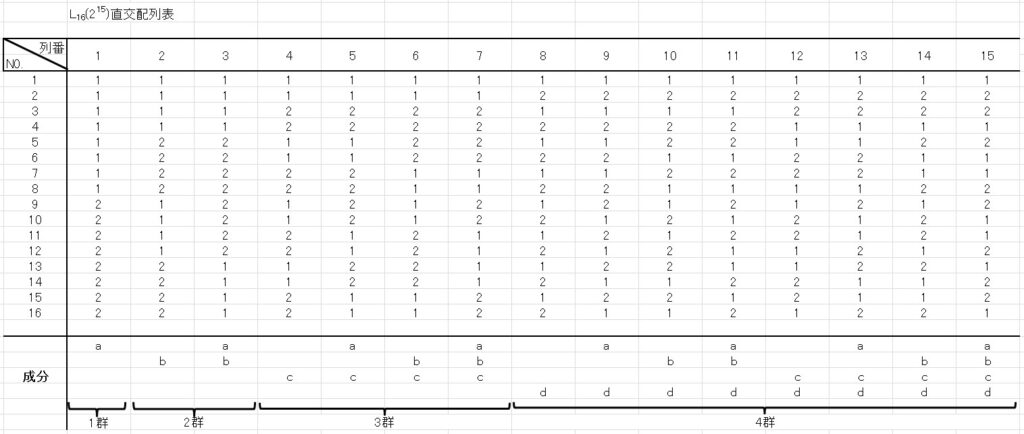
そこで、 \(L_{16}(2^{15})\) 直交配列表を使います。
\(L_{16}(2^{15})\) 直交配列表 は下表のとおりです。
\[\]
(´ºωº`)
下表のように各列に因子を割り付け、実験データ(右端)を得たとします。
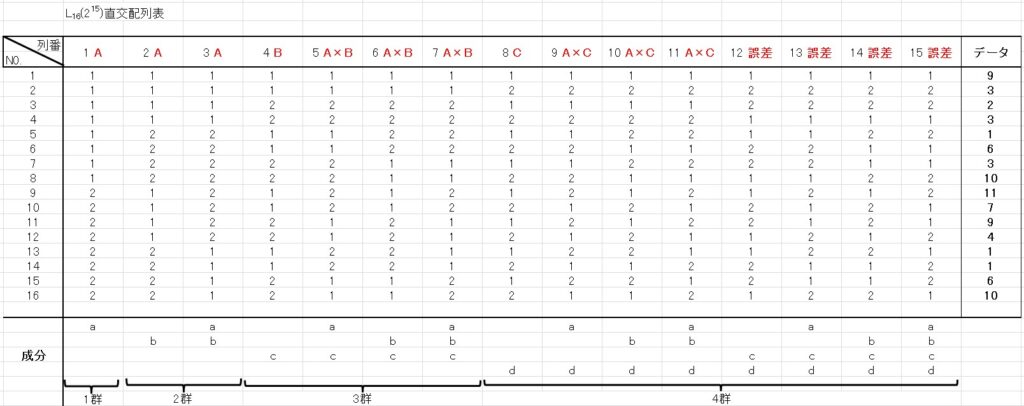
- 因子A :第1列、第2列、第3列
- 因子B :第4列
- 交互作用A×B:第5列、第6列、第7列
- 因子C :第8列
- 交互作用A×C:第9列、第10列、第11列
- 誤差 :第12列、第13列、第14列、第15列
\[\]
このままでは計算しづらいので、計算補助表を作ります。
計算補助表では、列ごとに第1水準の合計\(T_{[k]1}\) と第2水準の合計 \(T_{[k]2}\) を計算し、列平方和\(S_{[k]}\) を計算します。
列平方和の計算方法は、記事「 直交配列実験とは 2 2水準 」記載の下式で計算します。
\[S_{[k]}=\frac{{T_{[k]1}}^2}{N/2}+ \frac{{T_{[k]2}}^2}{N/2}-CT \qquad ⇒ \qquad \frac{(T_{[k]1}- T_{[k]2} )^2}{N} \]
※\(N\) はデータ数、つまり実験回数を表します。
今回は16回実験をおこなっているので、\(N=16\) となります。
\[\]
計算補助表は下表の通りです。

各列の列平方和 \(S_{[k]}\) が求められたので、各因子の平方和を計算すると、
- \(S_A=S_{[k=1]} +S_{[k=2]} +S_{[k=3]} =9+6.25+16=31.25\)
- \(S_B=S_{[k=4]} = 4\)
- \(S_{A \times B}=S_{[k=5]} +S_{[k=6]} +S_{[k=7]} =6.25+64+2.25=72.5\)
- \(S_C=S_{[k=8]} = 0.25\)
- \(S_{A \times C}=S_{[k=9]} +S_{[k=10]} +S_{[k=11]} =9+56.25+1=66.25\)
- \(S_{誤差}=S_{[k=12]} +S_{[k=13]} +S_{[k=14]}+S_{[k=15]} =9+2.25+0+6.25=17.5\)
\[\]
各因子毎の平方和を計算できたので、分散分析表を作って計算していきましょう。
\[\]
⑥多水準法での分散分析
「⑤多水準法での平方和」で計算した各因子の列平方和を分散分析表にまとめます。
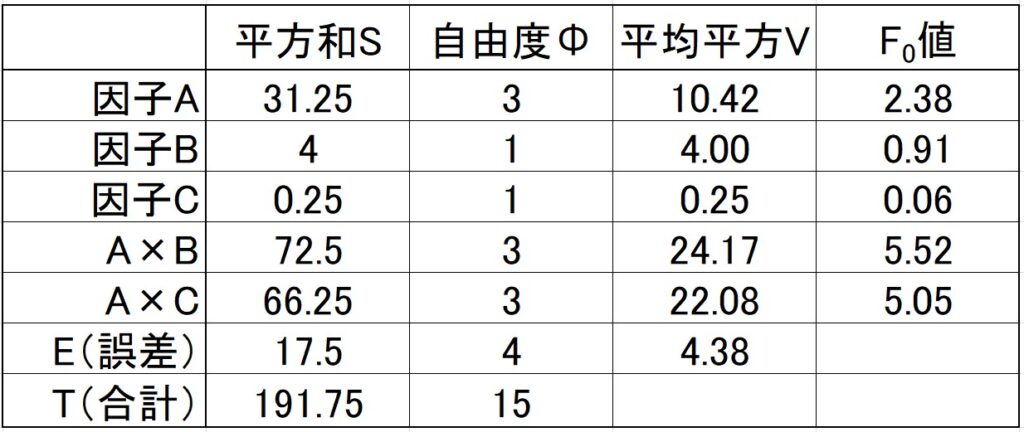
\[\]
前回の記事「直交配列実験とは 3 3水準」に記載したように、\(F_0\) 値が2以下の因子または交互作用をプーリングします。
要因配置実験と異なり、部分配置実験では因子もプーリングの対象になります。
すると、因子Bと因子Cがプーリングの対象になるのですが・・・
デスガ・・・(´・ω・`)?
\[\]
交互作用A×B、交互作用A×Cともに\(F_0\) 値が2よりも大きく、プーリングの対象ではありません。
しかし、交互作用がプーリングの対象にならない時は、その因子もプーリングの対象にしません!
つまり、因子Bと因子Cは残します。
φ(´・ω・`)メモメモ
\[\]
というわけで、分散分析表そのままに最適水準の決定や、最適水準における母平均の推定を行いましょう。
\[\]
⑦最適水準の決定
まずは、データの構造式を考えます。
分散分析の結果より、構造式は次のようになります。
\[\hat{\mu}(ABC)=\widehat{\mu + a+b+c+(ab)+(ac)}\]
\[=\widehat{\mu+a+b+(ab)}\qquad+\widehat{\mu+a+c+(ac)}\qquad-\widehat{\mu+a}\]
\[=\bar{x_{AB}}+\bar{x_{AC}}-\bar{x_{A}}\]
\[\]
今回は交互作用A×Bと交互作用A×Cがともに残っています。
最適水準を決める時は二元表を使いましょう。
今回の二元表は次のようになります。

二元表に書かれている数字は、同じ水準の実験のデータの和から求めます。
例えば、AB二元表のデータは、直交配列表のデータから下表のように求められます。

\[\]
(◉ω◉`) ジーーーッ
それでは二元表から最適水準を求めてみましょう。

\[\]
今回のデータでは因子A、因子B、因子Cと交互作用A×B、交互作用A×Cがあります。
交互作用のない因子では、その因子単独で最適水準を選べばよいのですが、今回はそのような因子はありません。
各因子の水準を選ぶときは、「全体としての最適水準」を選んでいきます。
(。´・ω・)?
\[\]
実験の結果より、交互作用はいずれも有意となり、交互作用A×Bと交互作用A×Cで共通の因子Aがあります。
AB二元表から因子Aの最適水準を選んでも、選んだ因子Aの水準がAC二元表を含めた「全体での最適水準」になるとは限りません。
ではどうすれ良いのか?というと、「共通する因子の水準を固定して」考えます。
\[\]
今回の場合は、データの構造式は以下の式で表されました。
\[\hat{\mu}(ABC)=\bar{x_{AB}}+\bar{x_{AC}}-\bar{x_{A}}\]
交互作用に共通する因子Aの水準を固定し、各条件での平均値を求め、最適水準を計算してみましょう。
\[\]
1)\(A_1\)水準で固定した場合
AB二元表より因子Bの最適水準は \(B_1\)、AC二元表より因子Cの最適水準は \(C_1\) となります。
この水準での平均値は、
\[\hat{\mu}(A_1B_1C_1)=\bar{x_{A_1B_1}}+\bar{x_{A_1C_1}}-\bar{x_{A_1}}\]
\[=\frac{12}{2}+\frac{11}{2}-\frac{17}{4}=7.25\]
※因子Aの水準1を満たすデータは4つあり、データの合計は「9+3+2+3=17」となります。
\[\]
2)\(A_2\)水準で固定した場合
AB二元表より因子Bの最適水準は \(B_2\)、AC二元表より因子Cの最適水準は \(C_2\) となります。
この水準での平均値は、
\[\hat{\mu}(A_2B_2C_2)=\bar{x_{A_2B_2}}+\bar{x_{A_2C_2}}-\bar{x_{A_2}}\]
\[=\frac{13}{2}+\frac{16}{2}-\frac{20}{4}=9.5\]
※因子Aの水準2を満たすデータは4つあり、データの合計は「1+6+3+10=20」となります。
\[\]
3)\(A_3\)水準で固定した場合
AB二元表より因子Bの最適水準は \(B_1\)、AC二元表より因子Cの最適水準は \(C_1\) となります。
この水準での平均値は、
\[\hat{\mu}(A_3B_1C_1)=\bar{x_{A_3B_1}}+\bar{x_{A_3C_1}}-\bar{x_{A_3}}\]
\[=\frac{18}{2}+\frac{20}{2}-\frac{31}{4}=11.25\]
※因子Aの水準2を満たすデータは4つあり、データの合計は「11+7+9+4=31」となります。
\[\]
4)\(A_4\)水準で固定した場合
AB二元表より因子Bの最適水準は \(B_2\)、AC二元表より因子Cの最適水準は \(C_2\) となります。
この水準での平均値は、
\[\hat{\mu}(A_4B_2C_2)=\bar{x_{A_4B_2}}+\bar{x_{A_4C_2}}-\bar{x_{A_4}}\]
\[=\frac{16}{2}+\frac{11}{2}-\frac{18}{4}=9\]
※因子Aの水準2を満たすデータは4つあり、データの合計は「1+1+6+10=18」となります。
\[\]
以上の結果から、全体での最適水準は「\(\hat{\mu}(A_3B_1C_1)\)」 となります。
次に、最適条件における母平均の推定を行ってみます。
\[\]
⑧最適条件における母平均の推定
最適条件における点推定値は「⑦最適水準の決定」で計算しました。
\[\hat{\mu}(A_3B_1C_1)=11.25\]
共通因子である因子Aの水準毎に最適水準を計算することで、結果的に最適水準の点推定値を計算しています。
\[\]
点推定値は計算しているので、信頼区間を計算するために有効反復係数\(n_e\)を計算します。
\[n_e=\frac{総データ数}{1+自由度の和}\]
\[=\frac{16}{1+3+1+1+3+3}\]
\[=\frac{16}{12}=\frac{4}{3}\]
自由度の和は「因子Aの自由度(3)+因子Bの自由度(1)+因子Cの自由度(1)+交互作用A×Bの自由度(3)+交互作用A×Cの自由度(3)」からなります。
\[\]
信頼率95%で区間推定を計算すると、
\[\hat{\mu}(A_3B_1C_1) \pm t(4,0.05)\sqrt{\frac{V_E}{n_e}}\]
\[=11.25 \pm t(4,0.05)\sqrt{\frac{3}{4}\times 4.38}\]
\[=11.25 \pm 2.776 \times 1.812\]
\[=11.25 \pm 5.030 \]
\[=6.22,16.28\]
※\(V_E\) は分散分析表より、 4.38 です。
\[\]
点推定値は11.25で、95%信頼区間は 6.22~16.28 となります。
\[\]
⑨母平均の差の推定
母平均の差は注意が必要です。
最適水準(\(A_3B_1C_1\))におけるデータの構造式を確認してみましょう。
\[\hat{\mu}(A_3B_1C_1)=\bar{x_{A_3B_1}}+\bar{x_{A_3C_1}}-\bar{x_{A_3}}\]
次に、比較として水準(\(A_3B_2C_2\))におけるデータの構造式を確認してみます。
\[\hat{\mu}(A_3B_2C_2)=\bar{x_{A_3B_2}}+\bar{x_{A_3C_2}}-\bar{x_{A_3}}\]
\[\]
この二つの水準「(\(A_3B_1C_1\))」と「(\(A_3B_2C_2\))」の差分を考えます。
すると、\(\bar{x_{A_3}}\) が打ち消し合うことがわかります。
この場合の有効反復係数は、
\[\frac{1}{n_e}=\frac{1}{2}+\frac{1}{2}=1\]
となります。
\[\]
有効反復係数がわかったので、二つの水準間の母平均の差を信頼率95%で区間推定すると、
\[\{\hat{\mu}(A_3B_1C_1)-\hat{\mu}(A_3B_2C_2)\}\pm t(\phi_E,0.05)\sqrt{\frac{2}{n_e}V_E}\]
\[=\{11.25-4.25\}\pm t(4,0.05)\sqrt{\frac{2}{1} \times 4.38}\]
\[=7\pm 2.776\times 2.960\]
\[=7 \pm 8.217\]
\[=-1.217,15.217\]
となります。
\[\]
点推定値は7.0 ですが、信頼区間に マイナス がついています。
どういうことでしょうか?
(。´・ω・)?
\[\]
これは二つの水準「(\(A_3B_1C_1\))」と「(\(A_3B_2C_2\))」の差分の平均が 7.0 で、たまに(\(A_3B_2C_2\))が実験結果で 1.217 ポイント逆転することを意味します。
“たまに”がどのくらいの確率かと言うと、2.5% です。
信頼率95%の区間推定をしているためです。
同じくらい”たまに(2.5%)” 母平均の差が 15.217 になります。
\[\]
最適水準を選んだからと言って、100%最適解になるとは限らないというわけです。
\[\]
⑩最適水準におけるデータの予測
最適水準おけるデータの予測は、今までと同じです。
今回の最適水準(\(A_3B_1C_1\)) の場合の「信頼率95%の区間予測の式」は次のようになります。
\[\hat{\mu}(A_3B_1C_1)\pm t(\phi_E,0.05)\sqrt{\left( 1+\frac{1}{n_e}\right)V_E}\]
\[=11.25\pm t(4,0.05)\sqrt{\left( 1+\frac{3}{4}\right) \times 4.38}\]
\[=11.25 \pm 2.776 \times \sqrt{\frac{7}{4}\times 4.38}\]
\[=11.25 \pm 2.776 \times 2.769\]
\[=11.25 \pm 7.687\]
\[=3.563, 18.937\]
\[\]
点推定値は11.25 で、信頼率95%の予測区間は 3.563~18.937 となります。
信頼区間よりも予測区間が大きくなる理由は、記事「 直交配列実験とは 2 2水準 」にまとめているので、ご参照ください。
\[\]
まとめ
①多水準法とは、4水準の因子を2水準の直交配列表に割り付ける方法のこと
②多水準法の大まかな手順は2水準法や3水準法と一緒
③多水準法の割り付けは、2水準の組み合わせで4水準を作る
④多水準法で使用する列は、交互作用の表れる列も使う
⑤多水準法での列平方和の計算方法は、2水準法と一緒
⑥多水準法での分散分析では、プーリング対象に注意!
⑦同じ因子が複数の交互作用に表れる場合は、水準を固定して考える
⑧最適水準における母平均の推定方法は、2水準法と一緒
⑨母平均差の推定では、データの構造式を考えること!
⑩予測区間は、信頼区間よりも大きくなるヨ
\[\]
今回も何だかんだ長い記事になってしまいました。(;´・ω・)
さすが1級ってことですかね、難しい!
次回は凝水準法について解説していきます。
\[\]













[…] 前回までは多水準法について学びました。 […]