直交配列実験とは　5　凝水準法

公開日2022年4月17日 　最終更新日 2022年12月19日

みなさんこんにちは、michiです。

前回までは多水準法について学びました。

今回は凝水準法について学んでいきます。

キーワード：「多水準法」

①凝水準とは

凝水準法とは、2水準の因子を3水準の直交配列表に割り付ける方法です。

基本的に3水準で、一部の水準が2水準の実験の場合に有効な手法となります。

\[\]

• 多水準法：4水準の因子を2水準の直交配列表に割り付ける
• 凝水準法：2水準の因子を3水準の直交配列表に割り付ける。

\[\]

②凝水準法の手順

凝水準法における分析の手順は、3水準直交配列実験と同じになります。

ただし、2水準の因子は一つ水準を重複させて3水準とします。

(。´･ω･)?

そこのところを解説していきます。

\[\]

ポイントは、「列平方和はそのまま使用しない」です。

\[\]

③凝水準法の割り付け

凝水準法では、（自由度1の）2水準因子を（自由度2の）3水準直交配列に割り付けると言いました。

…自由度が足りないですよね

(ｏ´･ω･)´-ω-)ｳﾝ

そこでどうするかと言うと、同じ水準を繰り返します。

\[\]

具体例として　因子A（2水準）、因子B(3水準)、因子C(3水準)、因子Ｄ(3水準)　を考えてみましょう。

\[\]

ここで同じ水準を繰り返した2水準因子をPとします。

この繰り返した水準を凝水準と言います。

交互作用が表れる列は、今まで学んできたように「成分」または「線点図」より求めることができます。

\[\]

次に平方和を計算していきます。

凝水準法では2水準因子の平方和を計算する際に、列平方和をそのまま使うことはできません。

例えば、\(L_{27}(3^{13})\) 直交配列表を用いて、2水準因子Ａの平方和\(S_A\) を求める計算式は、次のようになります。

\[S_A=\frac{(T_{A1})^2}{18}+ \frac{(T_{A2})^2}{9}-CT \]

\(T_{A1}\) は\(A_1\) 水準の和、\(T_{A2}\) は\(A_2\) 水準の和、CTは修正項を表します。

分母が第1項が 18、 第2項が 9　である理由は、全27回の実験の内、18回が 水準\(A_1\) で、9回が水準 \(A_2\) で実験を行っているためです。（下図）

\[\]

また、2水準因子と3水準因子に交互作用がある場合は

\[S_{AB}= \frac{(T_{A1B1})^2}{6}+ \frac{(T_{A1B2})^2}{6}+ \frac{(T_{A1B3})^2}{6}+ \frac{(T_{A2B1})^2}{3} + \frac{(T_{A2B2})^2}{3} + \frac{(T_{A2B3})^2}{3} -CT \]

を計算し、

\[S_{A \times B} = S_{AB}-S_A-S_B\]

から交互作用を計算します。

※\(S_B\)は列平方和と等しくなります。

\[\]

平方和を計算したあとの分散分析、プーリング、区間推定の手順は3水準直交配列実験と同じ方法で実施できます。

\[\]

④多水準法と凝水準法の組み合わせ

最後に多水準法と凝水準法を組み合わせた場合について考えていきます。

その前におさらいです。

\[\]

多水準法では、2水準の直交配列表に4水準因子を割り付ける方法を学びました。

2水準の直交配列表で2列(実質3列)使うことで、4水準を割り付けました。

\[\]

凝水準法では、3水準の直交配列表に2水準因子を割り付ける方法を学びました。

2水準のうち1つの水準を繰り返すことで、3水準の直交配列表に2水準因子を割り付けることができました。

3水準因子をPとすると、下図のようになります。

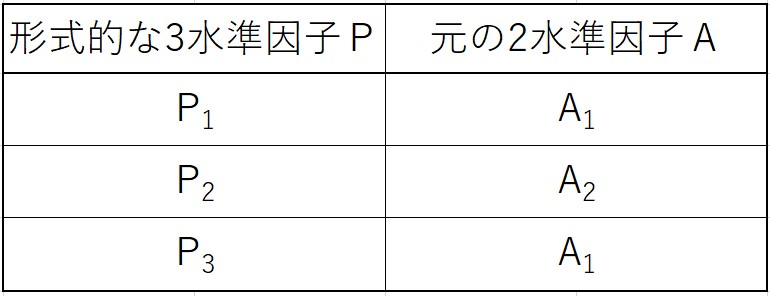
この場合、ほとんどの因子が3水準因子で、2水準因子が一部あるような状況になります。

\[\]

では、ほとんどの因子が2水準因子で、一部の因子に3水準因子があるような場合は、どのように考えればよいのでしょうか？

\[\]

(。´･ω･)?

答えは　「多水準法と凝水準法を組み合わせる」　です。

\[\]

まずは多水準法を用いて、4水準因子が割り付けられる用意をします。

次にその4水準を割り付けられる2列に凝水準法を使って、3水準因子を割り付けます。

\[\]

イメージは、大きめの箱を用意（多水準法）して、箱よりも小さいものを入れる（凝水準法）と考えましょう。

\[\]

次に要因平方和を計算します。

ただし、凝水準法を使っているので、列平方和をそのまま使うことはできません。

凝水準法で学んだように、個別に計算します。

\[\]

一般化した式は以下の通りです。

\[S_A=\sum_{i=1}^{n} \frac{(水準A_i の和)^2}{ 水準A_i のデータ数}- \frac{(合計)^2}{総データ数}\]

\[S_B=\sum_{i=1}^{n} \frac{(水準B_i の和)^2}{ 水準B_i のデータ数}- \frac{(合計)^2}{総データ数}\]

\[S_{AB}= \sum_{i=1}^{n} \sum_{j=1}^{m} \frac{(水準A_iB_j の和)^2}{ 水準A_iB_j のデータ数}- \frac{(合計)^2}{総データ数} \]

\[S_{A\times B}=S_{AB}-S_A-S_B\]

\[\]

誤差平方和は、総平方和から要因平方和を引いて求めることができます。

凝水準法を使うと、誤差列以外にも誤差が表れます。

(´・∀・｀)ﾍｰ

\[\]

そのため、要因分析の時と同じように、分散分析表を作成し、F値の計算を行います。

分散分析の結果、プーリングが必要であればプーリングを行い再度分散分析を行います。

有意となった因子や交互作用の最適水準で信頼区間や予測区間を求めましょう。

\[\]

⑤多水準法と凝水準法の計算問題

それでは実際に多水準法と凝水準法を組み合わせた直交配列実験の例を解いてみます。

取り上げる水準は以下の通りです。

• 因子A：3水準
• 因子B：2水準
• 因子C：2水準
• 因子D：2水準
• 交互作用　A×B
• 交互作用　A×C
• 交互作用　B×C

\[\]

実験データは以下の通りです。

(つд⊂)ｺﾞｼｺﾞｼ

見づらくて申し訳ない…

\[\]

因子の割り付け

因子Aの水準数が3なので、水準１を重複させて、因子P（4水準）とします。（凝水準法）

つぎに、4水準の因子を2水準の直交配列表に割り付けます。（多水準法）

\[\]

因子Pは4水準＝自由度3なので、2水準直交配列表の3列を使って割り付けを行います。

※2水準直交配列表の1列あたりの自由度は1

今回は列番[１][２][３]に因子Pを割り付けてみます。

\[\]

次に、因子Bを列番[４]に割り付けます。

すると、因子Pとの交互作用P×Bは、列番[５][６][７]に表れます。

なぜ列番[５][６][７]に交互作用が表れるかというと、成分に着目するとわかります。

\[\]

次に、因子Cを列番[８]、因子Dを列番[１３]に割り付け、列番[１４][１５]は誤差列となります。

列番[９][１０][１１]は因子Pと因子Cの交互作用が表れる列となります。

また、列番[１２]は因子Bと因子Cの交互作用が表れる列になります。

まとめると、下表のようになります。

\[\]

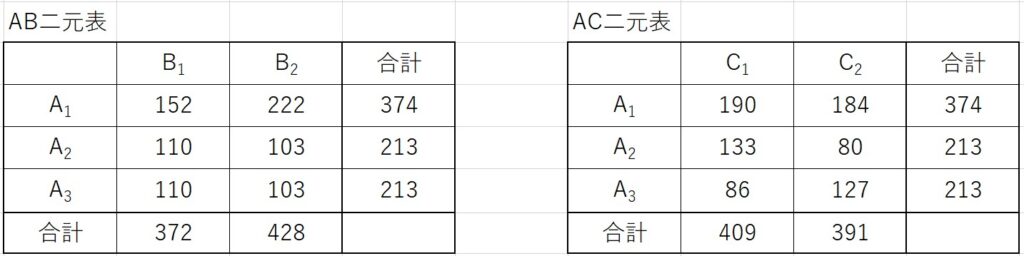
この時のAB二元表、AC二元表は下図のようになります。

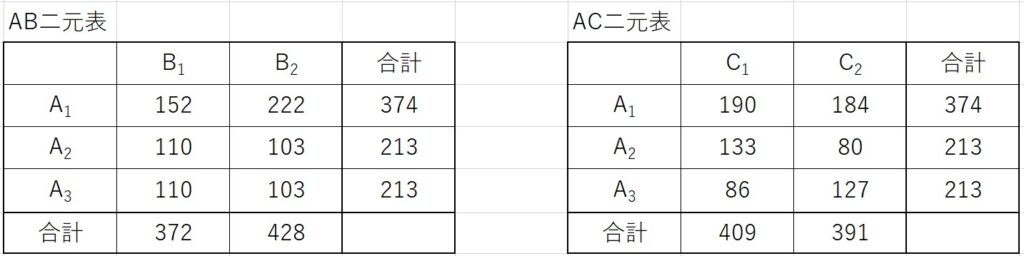
また、各水準の和と列平方和を計算した結果は下表のようになります。

\[\]

平方和の計算

次に平方和を計算しますが、列平方和をそのまま使える因子とそのまま使えない因子があります。

そのまま使えない因子は、因子P（因子A）とその交互作用のP×B（交互作用A×B）、P×C（交互作用A×C）になります。

実験計画法で計算した時と同様に、因子A及びその交互作用を計算します。

\[\]

①修正項 \(CT\) の計算

\[CT=\frac{800^2}{16}=40000\]

②総平方和 \(S_T\) の計算

\[S_T=(32^2+39^2+…+55^2+63^2)-CT\]

\[=42286-40000\]

\[=2286\]

※各データの二乗の合計から修正項 \(CT\) を引きます。

③因子Aの要因平方和

\[S_A=\frac{374^2}{8}+\frac{213^2}{4}+\frac{213^2}{4}-CT\]

\[=40169-40000\]

\[=169\]

※第一項は8回分の実験データから算出されるため、分母が8になります。

④因子Bの要因平方和

因子Bの要因平方和は列平方和と同じになります。

因子Bは第[４]列に割り付けましたので、表から読み取って・・・

\[S_B=196\]

⑤因子ABの要因平方和

因子ABの要因平方和は、AB二元表のデータから計算します。

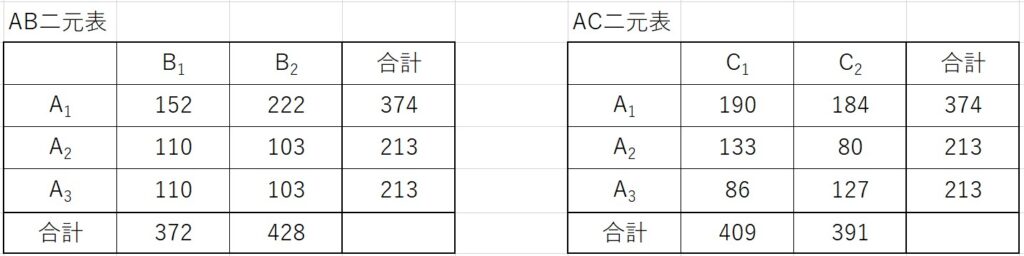
\[S_{AB}=\frac{152^2}{4}+\frac{222^2}{4}+\frac{110^2}{2}+\frac{103^2}{2}+\frac{110^2}{2}+\frac{103^2}{2}-CT\]

\[=40806-40000\]

\[=806\]

※第一項の分母が4である理由は、\(A_1B_1\)の条件のデータが4個あるためです。

　第二項も同様に分母が4になります。

\[\]

⑥交互作用\(S_{A \times B}\)の要因平方和

②から⑤までの要因平方和の計算から、交互作用の要因平方和を計算すると…

\[S_{A \times B}=S_{AB}-S_A-S_B\]

\[=806-169-196\]

\[=441\]

\[\]

⑦交互作用\(S_{A \times C}\)の要因平方和

②から⑥までの計算を因子Aと因子Cでも計算します。

すると、

\[S_A=169\]

\[S_C=20.25\]

\[S_{AC}=1296\]

\[S_{A \times C}=1106.75\]

となります。

\[\]

⑧交互作用\(S_{B \times C}\)の要因平方和

交互作用\(S_{B \times C}\)の要因平方和は列平方和から確認できます。

因子Bは第[４]列に、因子Cは第[８]列に割り付けているため、その交互作用は第[１２]列に表れます。

\[S_{B \times C}=0.25\]

\[\]

分散分析表の計算

各平方和の計算結果を分散分析表にまとめると、下表のようになります。

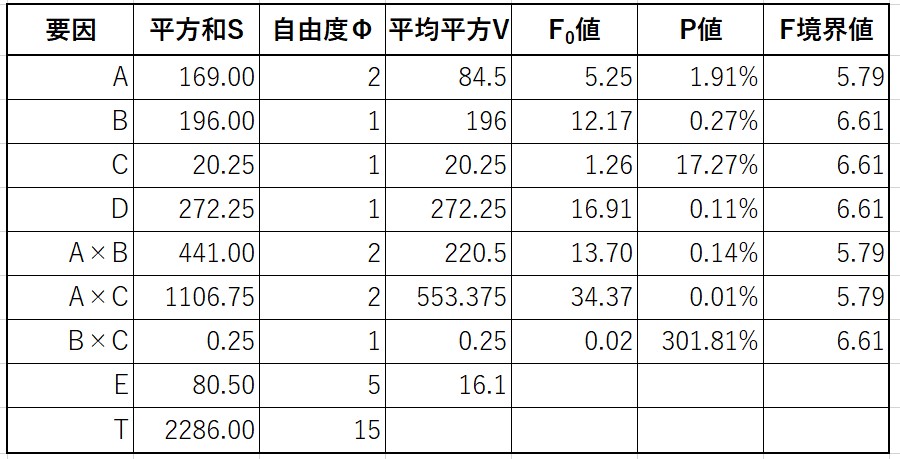
分散分析表の作り方や計算方法の詳細は記事「実験計画法1　一元配置実験」をご参照ください。

F境界値は有意水準 α=5% の時の値です。

\[\]

Eは誤差を表します。

誤差の自由度が 5 となっています。

直交配列表での誤差列は2列しか割り付けていないのに、残りの3列はどこからきたのでしょうか・・・

(。´･ω･)?

答えは、「因子Aからくる」です。

因子Aは凝水準法を使って、直交配列表に割り付けを行っています。

凝水準法を使うと、誤差列以外にも誤差が表れます！

\[\]

誤差平方和\(E\) は、総平方和\(S_T\) から各要因平方和を引くことで求めます。

※誤差の自由度も同様に、全体の自由度から各因子の自由度を引いて求めます。

\[\]

つぎにプーリングを考えます。

分散分析表を見ると、因子Aと因子C、交互作用B×Cの \(F_0\) 値がF境界値よりも小さいです。

ただし、因子Aについては \(F_0\) 値が2.0大きいため、プーリング対象とはしません。

また、因子Cも因子Aとの交互作用A×Cが有意となりそうなため、プーリング対象とはしません。

((φ(-ω-｀*)ﾒﾓﾒﾓ

\[\]

よって、交互作用B×Cのみをプーリング対象として、分散分析表を作り直します。

すると・・・

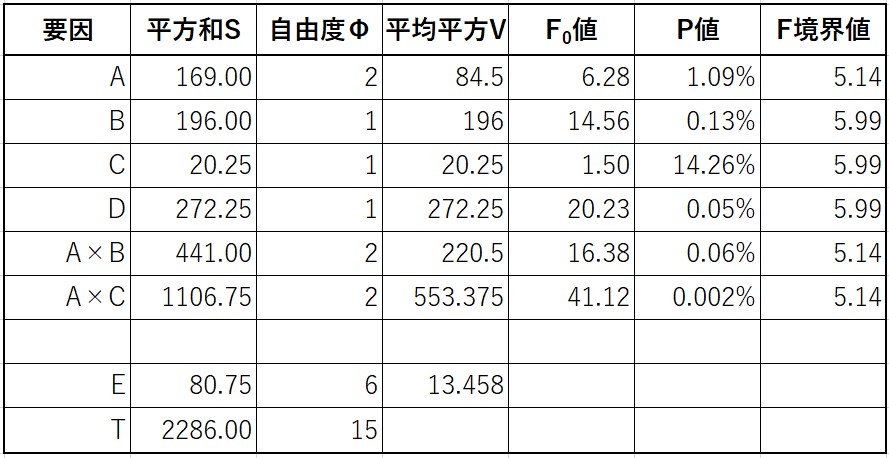
分散分析表から、

因子B、因子D、交互作用A×B、交互作用A×Cは高度に有意となり、因子Aは有意となります。

因子Cは有意とはなりませんでしたが、交互作用A×Cが有意であるため、プーリングしません。

\[\]

最適水準の決定と母平均の推定

分散分析までできたので、最適水準の決定と母平均の推定を行います。

最適水準はAB二元表、AC二元表および列平方和の計算結果から、

\(A_2B_1C_1D_2\) となります。

\[\]

(。´･ω･)?

AB二元表とAC二元表を見ると、因子Aの最適水準は \(A_1\) のように見えます。

しかし、水準\(A_1\)のデータは4個分のデータであることを思い出してください。

水準\(A_2\)と水準\(A_3\)のデータは2個分のデータなので、倍あります。

そのため、最適水準を考える時は、水準\(A_1\)のデータは半分にして考えます。

\[\]

それでも \(A_1B_2>A_2B_1,A_3B_1\)　です。

その差は 1 です。

あまり大きな差とは言えないですよね。

ここで、もう一つの有意な交互作用A×Cについて考えます。

AC二元表をみると、\(A_2C_1\)が最適水準であることがわかります。

AC二元表の結果から因子Aの最適水準を\(A_2\)とすると、AB二元表から因子Bの水準は\(B_1\)であることがわかります。

\[\]

最後に因子Dですが、因子Dは第[１３]列に割り付けました。

列平方和の結果から、\(D_2\)が最適水準をであることがわかります。

\[\]

データの構造式から最適水準を計算すると・・・

\[\widehat{A_2B_1C_1D_2}=\widehat{\mu+a_2+b_1+c_1+d_2+(ab)_{21}+(ac)_{21}}\]

\[=\widehat{\mu+a_2+b_1+(ab)_{21}} \qquad +\widehat{\mu+a_2+c_1+(ac)_{21}} \qquad +\widehat{\mu+d_2}-\hat{\mu}-\widehat{\mu+a_2}\]

\[=\frac{110}{2}+\frac{133}{2}+\frac{433}{8}-\frac{800}{16}-\frac{213}{8}\]

\[ \approx 72.38\]

分数の計算では、それぞれのデータ数で割り算して計算します。

例えば、\(\widehat{\mu+d_2}\) では、433というデータは8回分の実験データの合計なので、8で割ります。

\[\]

有効反復係数 \(n_e\) は、伊奈の式から

\[\frac{1}{n_e}=\frac{1}{2}+\frac{1}{2}+\frac{1}{8}-\frac{1}{16}-\frac{1}{4}\]

\[=\frac{13}{16}\]

\[\]

信頼率95%での信頼区間を計算すると

\[\hat{\mu}(A_2B_1C_1D_2) \pm t(\phi_E,\alpha)\sqrt{\frac{V_E}{n_e}}\]

\[=72.38 \pm t(6,0.05)\sqrt{\frac{13}{16} \times 13.458}\]

\[=72.38 \pm 2.447 \times 3.306 \]

\[=72.38 \pm 8.09\]

\[=64.29 , 80.47\]

\[\]

データの予測

最後にデータの予測を行いましょう。

((((;´･ω･`)))ｶﾞｸｶﾞｸ

といっても、恐れる必要はありません。

有効反復係数の計算部分に 1　を追加するだけです。

それでは、計算してみましょう。

\[\]

\[\hat{\mu}(A_2B_1C_1D_2) \pm t(\phi_E,\alpha)\sqrt{\left(1+\frac{1}{n_e}\right)V_E}\]

\[=72.38 \pm t(6,0.05)\sqrt{\left(1+\frac{13}{16} \right)\times 13.458}\]

\[=72.38 \pm 2.447 \times 4.938 \]

\[=72.38 \pm 12.08\]

\[=60.3 , 84.46\]

\[\]

やり方のパターンさえ覚えてしまえば、あとは作業なのでやるだけです。

とはいえ、そのやり方がわからない・・・

ということで、当ブログを何度も読み返しましょう！

( `･д･)っ))ﾅﾝﾃﾞﾔﾈﾝｯ

\[\]

まとめ

①凝水準法とは、2水準の因子を3水準の直交配列表に割り付けること

②凝水準法では、列平方和をそのまま使用しない！

③凝水準法の割り付けでは、同じ水準を繰り返す

④多水準法と凝水準法を組み合わせて、「ほとんどの因子が2水準因子で、一部の因子に3水準因子があるような場合」の割り付けが可能！

⑤多水準法と凝水準法の計算問題は、とにかく反復して覚えましょう！

\[\]

今回は凝水準法と凝水準法＋多水準法について学びました。

ここまでくると専門性がかなり上がって厄介になってきますね。

とはいえ、実験回数が多くなってくると直交配列表による分析はかなり有効になります。

諦めずにトライしましょう！

※QC検定ではここまで深い内容はでないカモ…🦆

\[\]

⇒オススメ書籍はこちら

⇒サイトマップ